На современном этапе технологического и социального развития общества и наряду с процессами всеобщей глобализации обработка и передача информации между различными подсистемами становится неотъемлемой частью любого сложного процесса или системы. В связи, с чем возникает необходимость в разработке инвариантного метода к анализу сложных систем обработки информации (СОИ), в качестве которого можно применить тензорный метод двойственных сетей, позволяющий формализовать процедуру описания математической модели распределенных систем обработки информации на основе матричной алгебры.
Вне зависимости от типа системы обработки информации, ее функций и сложности структуры и так как сама СОИ может состоять из произвольного числа СОИ ее математическую модель можно представить простым уравнением [3,4]:
или
(1)
где
ρ – загрузка СОИ;
λ – среднее значение интенсивности поступления требований в СОИ;
μ – интенсивность обслуживания требований в СОИ;
t =1/ μ – среднее время обслуживание одного требования в СОИ.
Согласно первому постулату обобщения тензорного метода сложных систем, предложенного Г. Кроном [2], если известно аналитическое выражения для простейшего элемента, то и математическая модель системы будет описываться таким же уравнением, только записанном в матричном виде. Тогда на основании первого постулата математическая модель распределенной системы обработки информации (РСОИ), как совокупности СОИ с учетом математической модели простейшего элемента (1), будет описана формулами:
(2)
или
, (3)
где
Р – вектор загрузок РСОИ;
– вектор интенсивностей поступления требований в РСОИ;
М – матрица интенсивностей обслуживания требований в РСОИ;
T – матрица времени обслуживания.
Согласно тензорному методу двойственных сетей, предложенному Петровым А.Е. [4], любую сложную систему можно рассматривать как двуединую сеть, где понятие сеть шире, чем понятие граф, согласно [4] сеть - это инвариантная структура с постоянным количеством ветвей, проекциями которой являются все возможные комбинации графов с таким же количеством ветвей. Данная сеть описывается набором тензоров с поперечными и продольными компонентами. Описать компоненты тензора можно, только в том случае, если задан базис пространства, в котором этот тензор существует, иными словами тензор можно описать его проекциями в различных базисных системах координат. Следовательно, с позиции тензорного анализа двойственных сетей РСОИ уравнение (2 и 3) следует понимать как инвариантное уравнение относительно системы координат (второй постулат Г.Крона [3]), компонентами которого являются поперечный тензор 
, продольный тензор Р.
Базисом конкретной проекции сети служит система линейно-независимых контуров и система линейно-независимых разрезов/открытых путей, контура и разрезы задаются соответственно матрицей разрезов и контуров, которые, как известно, ортогональны друг другу [5], поэтому полная размерность пространства линейно-независимых компонент остается постоянной и равной количеству ветвей сети. Основным недостатком теории Г.Крона было предположение об инварианте рассеиваемой мощности электрической сети при изменении ее структуры, что для произвольных систем выражалось бы в постоянстве скалярного произведения тензора продольных и поперечных компонент для произвольных проекций одной сети, в свою очередь выполнение инварианта мощности не происходит при изменении структуры. Такой инвариант существует для двух двойственных сетей [1].
Для произвольной сети, состоящей из n ветвей можно выделить особую проекцию такой сети в виде несвязанного графа, в терминологии Г. Крона такие сети называются примитивными (рисунок 1), узловая примитивная сеть является двойственной сетью к примитивной контурной и наоборот. Для таких сетей матричное уравнение имеют тривиальный вид (4).
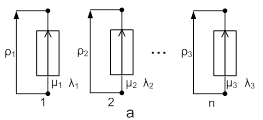
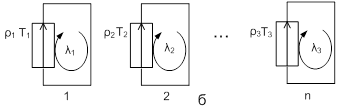
Рисунок 1 – Примитивная n-мерная сеть: а-узловая, б-контурная
а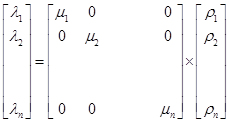 
б 
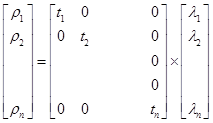(4)
Формула 4а является математической моделью примитивной узловой сети 4б – примитивной контурной сети.
Согласно тензорному анализу двойственных сетей сумма линейно-независимых разрезов или контуров для сети и ей двойственной является неизменной величиной в независимости от топологии. Это означает, что все множество линейно-независимых контуров или разрезов всевозможных проекций одной сети представляет собой полную группу, откуда следует, что всегда существует правило перехода от одного базисного набора контуров или разрезов одной проекции сети к другому базисному набору другой проекции сети. Как известно переход от одного базиса к другому задается с помощью матрицы перехода, эта же матрица служит преобразованием координат для произвольного вектора. Если в качестве базиса для сети задаться набором линейно-независимых контуров, то для примитивной сети все контура будут находиться в одной из двойственных сетей, следовательно, каждая контурная интенсивность будет равна интенсивности потока в соответствующей ветви, а матрица линейно независимых контуров будет представлять собой единичную матрицу. После изменение структуры сети часть базисных контуров будет находиться в одной сети, а другая часть в её двойственной, но их количество при этом останется неизмененным, а матрица перехода от базиса примитивной сети к новому базису будет совокупностью двух матриц линейно-независимых контуров новой сети. Связь же контурных интенсивностей примитивной сети и контурными интенсивностями новой (исследуемый) сети будет следующей:
, (5)
где
- контурные интенсивности примитивной сети
- контурные интенсивности двух двойственных сетей.
С – матрица перехода.
При этом:
, (6)
где С1 - матрица линейно-независимых контуров исследуемой сети, С2 – матрица линейно-независимых контуров двойственной к исследуемой сети.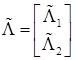 
, где 
- контурные интенсивности исследуемой сети, 
- контурные интенсивности двойственной сети. Таким образом, формулу (5) можно записать как:
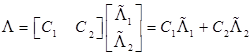(7)
С практической точки зрения процессы, происходящие в двойственной по отношению к исследуемой сети, не важны, поэтому достаточно знать преобразование контурных интенсивностей примитивной сети в контурные интенсивности исследуемой сети, таким образом, допустимо следующее преобразование:
(8)
Таким образом, выражение (8) показывает связь структур примитивной сети и исследуемой. Рассмотрим связь тензоров контурных загрузок примитивной сети и исследуемой сети. Под контурной загрузкой понимается загрузка, создаваемая контурной интенсивностью, для примитивной сети эта загрузка равна загрузке соответствующей системе обработки информации, то есть имеет конкретный физический смысл.
Рассмотрим скалярное произведение тензоров примитивной сети 
, при изменении структуры сети произведение контурных величин должно оставаться инвариантным относительно преобразования базисов, то есть:
(9)
Подставляя в выражение (8) в выражение (5) получаем 
, с учетом правил перестановки матриц 
, сравнивая левую и правую часть последнего выражения окончательно связь контурных загрузок можно записать как:
(10)
С учетом (5) выражение (9) можно записать как: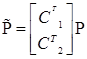 
или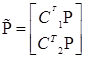 
, принимая во внимание, что связь двойственной сети с примитивной не имеет практической значимости для исследования процессов в реальной системе, то окончательное преобразование будет следующим:
(11)
Для связи матриц времени обслуживания примитивной и новой исследуемой сети подставим в (11) формулу (3)
(12)
Согласно второму постулату обобщения можно записать что:
(13)
В формулу (13) подставим вместо 
значение 
(14)
Как видно из (14) матрицы времени обслуживания двух сетей связаны следующим соотношением:
(15)
После определения значения матрицы 
по формуле (15) и значения загрузок 
по формуле (11) найдем контурные интенсивности исходной сети:
(16)
После определения контурных интенсивностей, определяем значения интенсивностей и загрузки в ветвях исходной сети как:
(17)
(18)
Для упрощения вычислений контурных значений исследуемой сети и упрощения вычислений в целом в формулах 11 и 15 вместо матрицы 
можно использовать модифицированную матрицу перехода 
, в матрице все линейно-зависимые строки равны нулю. Определить линейно-зависимые строки в матрице просто, если матрица была определена как транспонированная матрица фундаментальных циклов, так как каждый фундаментальный цикл такой матрицы включает только одно ребро не входящее в остов графа исследуемой сети. Саму же матрицу фундаментальных циклов можно получить из матрицы инцидентности исследуемой сети, найдя ортогональную ей матрицу. Из сказанного следует, что:
(19)
(20)
Конечным результатом анализа является система уравнений, связывающая загрузки в каждой ветви исследуемой сети через загрузки в линейно-независимых ветвях исследуемой сети, или потоки в каждой ветви через потоки в линейно-независимых ветвях.
Если учесть независимость состояний каждой СОИ в исследуемой сети, то можно сформулировать следующую задачу оптимизации: найти такое распределение информации по системам обработки информации, чтобы минимизировать суммарное время обработки информации находящейся в распределенной системе. Для решения такой задачи необходимо знать зависимость времени обработки информации в зависимости от загрузки или интенсивности поступления информации СОИ, если такая зависимость установлена, то целевая функция, минимум которой необходимо найти, будет иметь следующий вид:
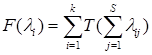, (21)
где
- интенсивность i–й СОИ, создаваемая источником j, определяется из формулы (18);
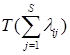- время обработки информации в СОИ;
S – количество источников информации, чьи запросы должна обслуживать распределенная система обработки информации. Ограничением является 
для
.
Как правило, функция 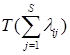является выпуклой, а, следовательно, целевая функция (21) будет выпуклой и иметь один глобальный минимум в области ограничений.
В данной статье был представлен метод исследования контурной модели распределенных систем обработки информации, а также предложен метод оптимизации таких систем с целью уменьшения времени обработки информации на основе тензорного метода анализа двойственных систем. На сегодняшний день, в связи с тем, что необходимо управлять процессом обработки множества информационных потоков с заданным качеством обслуживания для каждого типа потока в большом количестве систем, составляющих систему обработки информации, решение задачи управления по использованию ресурсов таких систем значительно усложняется. Тензорный метод анализа сетей позволяет уменьшить задержки при динамическом управлении сложными системами и обеспечить хорошую масштабируемость, так как обладает возможностями по учету взаимодействия внутрисетевых процессов и структуры сети. Результатом работы является то, что получаемая с помощью тензорного анализа целевая функция определяется в явном виде, а ограничения задаются матрицей интенсивностей, что приводит к тому, что минимум такой целевой функции может быть найден любым методом динамического или нелинейного программирования. Кроме того, методика получения оптимального решения с помощью тензорного анализа является хорошо формализованной задачей с невысокой вычислительной сложностью [1], что позволяет повысить качество обслуживания информационных потоков в любых распределенных системах обработки информации и обеспечить снижение суммарного времени обработки.
Рецензенты:
1. Петров М.Н. д.т.н. профессор, зав. кафедрой «Электронной техники и телекоммуникации» Сибирский государственный аэрокосмический университет им. академика М.Ф. Решетнева, г. Красноярск.
2. Увайсов С.У. д.т.н. профессор, зав. кафедрой «Радиоэлектроники и телекоммуникаций» Московский институт электроники и математики Национальный исследовательский университет Высшая школа экономики