Введение. Внедрение методов математического моделирования в обучение школьников
Новые проекты стандартов школьного образования [3] предполагают использование компьютерных технологий и методов математического моделирования в обучении школьников.
Информационные и коммуникационные технологии, являясь одной из составляющих предмета подготовки будущего учителя математики и информатики, открывают возможности для создания эффективных методов и форм обучения, основанных на их использовании.
Осуществляя педагогическую деятельность, преподаватель (учитель) должен не только приобщить обучаемых к использованию информационных технологий в рамках учебного процесса, но и сориентировать на использование информационных технологий при решении жизненных задач. Основным подходом к внедрению новых школьных образовательных стандартов мы считаем использование в качестве методологической основы при разработке образовательных программ концепцию деятельностного подхода. В соответствии с ней предметные (математические и информационно-компьютерные) и методические знания будущих учителей переплетаются в учебном процессе и направлены на умение решать прикладные задачи и использовать эти умения в процессе математического и компьютерного моделирования реальных процессов.
Рисунки 1 и 2 иллюстрируют различия между традиционным обучением и инновационном, предлагаемом в нашем подходе подготовки учителей математики и информатики.
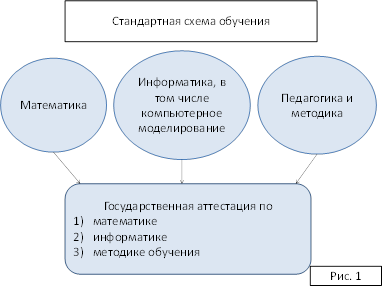
Рис. 1. Стандартная схема обучения
При подготовке учителей по традиционной схеме каждая дисциплина преподается в отдельности, без учета междисциплинарных связей, студенты не обучаются использованию полученных знаний и не готовы к самостоятельной деятельности.
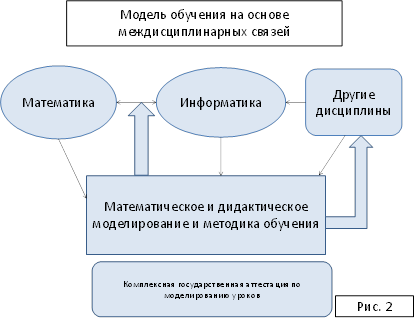
Рис. 2. Междисциплинарная схема обучения
При подготовке учителей на основе междисциплинарных связей основное внимание уделяется решению задач, направленных на построение моделей, тем самым возникают обратные связи, стимулирующие изучение, как самого предмета – объекта моделирования, так и математики и информатики, играющих роль инструментов познавательного процесса.
Например, рассмотрим следующую задачу: "Составить математическую и компьютерную модель солнечной системы". Эту задачу способен решить как школьник старших классов, так и студент университета. Только решать ее они будут по-разному, в соответствии с уровнем своих знаний и представлений. Некоторые школьники, например, могут в качестве орбит планет взять окружности, другие прочитают в научной литературе, что орбитами планет являются эллипсы, а студенты задумаются о влиянии сил притяжения планет друг к другу... Но всех их будет объединять одно: чтобы решить эту задачу, необходимо повторить и изучить дополнительную литературу по физике, астрономии, математике, составить математическую модель, найти соответствующую компьютерную программу. Данный поиск информации приводит к возникновению процесса установления междисциплинарных связей (рис. 2). Таким образом, решение такого рода задач способно создавать дополнительные стимулы к самостоятельной поисковой, познавательной и учебной деятельности, для развития мотивации, психологической самостоятельности учащихся.
Любая используемая программа для обучения должна быть естественным продолжением (обобщением) материала лекции, практического или лабораторного занятия. Поэтому преподаватель должен иметь возможность сам определять структуру и методические особенности программы. Более того, программа должна быть легко модифицируемой (изменяемой), причем желательно, чтобы эти изменения мог вводить сам педагог. В идеале – программа должна быть создана самим преподавателем (либо группой преподавателей, объединенных общими методическими целями).
Создание новых курсов по междисциплинарным связям и математическому моделированию – уже десятилетие находятся в центре пристального внимания авторов инноваций в области образования.
Авторы данной статьи рассмотрели возможность использования компьютера при разрешении ряда проблемных ситуаций, возникающих при обучении геометрии и ряда вопросов междисциплинарной связи геометрии и других дисциплин.
Проблемные ситуации при обучении геометрии и междисциплинарные связи
Развитие пространственных представлений учащихся является одной из важных задач школьного курса геометрии. Актуально решение этой проблемы также в ряде смежных дисциплин: рисовании, черчении, географии, физики, химии и др. Однако в настоящее время многие учителя и методисты указывают на невысокий уровень пространственного воображения и пространственного мышления школьников [2]. Систематическая работа над формированием и развитием пространственных представлений приводит к улучшению ситуации только тогда, когда используется сочетание традиционных методов и компьютерных информационных технологий.
Для успешного изучения курса геометрии одним из необходимых условий является умение мысленно представлять геометрические образы в пространстве. Решение геометрических задач «в воображении» в школе практически не используется. Отсюда, при переходе от планиметрии к изучению курса стереометрии у учащихся возникает немало трудностей при оперировании трехмерными объектами.
Решается эта задача несколькими способами. На начальной ступени образования геометрических представлений находят свое применение модели геометрических тел. После этого включаются в работу упражнения, которые направлены на оперирование мысленными представлениями геометрических фигур. В этом случае возникает ряд проблемных ситуаций (в области оперирования пространственными представлениями, соотношениями и зависимости), связанных с тем, что многие схематические изображения статического характера требуют в процессе их чтения оперирования динамическими пространственными образами. Компьютер может помочь ученику сделать первый шаг, позволив увидеть процесс создания искомого образа на экране.
При выборе того или иного программного обеспечения необходимо учитывать степень его освоенности педагогической средой. Это приводит как к более быстрому обмену опытом, так и к созданию творческих объединений учителей и преподавателей вузов, объединенных общими методическими целями.
К решению проблем обучения геометрии могут помочь компьютерные математические пакеты. Но какие математические пакеты можно внедрить при изучении геометрии в школе? Наиболее популярные математические пакеты в России являются Maple, MathCAD, MathLAD, Mathematica [2]. Но внедрить эти пакеты в школу затрудняет несколько факторов: дороговизна их лицензий; интерфейс состоит из ввода команд, которые учащиеся должны дополнительно изучать, а это драгоценное время учителя и ученика. Предпочтение дается бесплатным или уже имеющимся в вооружении учителя математическим пакетам. Речь идет о GeoGebra и программы учебно-методический комплект (УМК) «Живая Математика» (ЖМ), который сформирован на основе программы Geometry’s Sketchpad (в русском переводе «Живая Математика»), разработанной фирмой Key Currculum Press (USA), переведенной на русский язык и адаптированной Институтом новых технологий [5]. Комплект был поставлен в школы Российской Федерации в рамках ПНПО. Две программы по технической начинке очень похожи, но GeoGebra является бесплатным ПО в отличие от ЖМ. Это преимущество не так и важен, так как у программы ЖМ уже есть лицензия в школах РФ.
У Geo Gebra имеется различные инструментарии, такие как “многоугольники” и “каноническое сечение”, которые в ЖМ отсутствуют. Но это в свою очередь можно использовать для мотивирования учащихся к построению дополнительных чертежей, которые развивают у них творческие способности. Ниже приводим принципы построения изображений стереометрических фигур, с использованием программы «Живая Математика».
Для создания имитации вращения стереометрических фигур относительно заданной оси необходимо помнить, что точки фигуры при вращении описывают окружность на плоскости, перпендикулярной относительно оси вращения. При параллельном проецировании окружности на какую-нибудь плоскость получаем ее изображение в общем случае в виде эллипса. У GeoGebra этот инструмент есть, а у ЖМ нет. Проблему построения эллипса в программе ЖМ можно решить следующим образом:
1. Построить вертикальную прямую k.
2. В этой прямой взять точку О. Эта точка будет центром двух окружностей.
3. Построить прямую, проходящую через точку О и произвольную точку В, которая лежит в большой окружности. Пересечение полученной окружности с маленькой окружностью отмечаем буквой А.
4. Через точку В нужно построить параллельную прямую m к прямой k, с помощью инструмента построения.
5. Через точку А к прямой m нужно построить перпендикуляр n с помощью инструмента построения.
6. Пересечение m и n обозначаем буквой С.
7. Пусть точка В движется по окружности против часовой стрелки (для этого нужно отметить точку В и Правка-Кнопки-Анимация-ОК).
8. Нужно отметить точки С и В и нажать кнопку Геометрическое место (эта кнопка находится в Построении).
9. После этого нужно скрыть все вспомогательные элементы (нужно выделить все элементы и Вид – Cкрыть объекты).
10. Искомый эллипс перед вами.
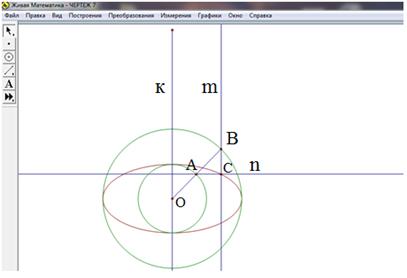
Рис. 3. Динамический чертеж, в программе “Живая Математика”
геометрическое место точек эллипса
Наибольшую значимость этот инструмент имеет при создании изображений стереометрических чертежей. Чтобы фигура вращалась, нужно вершины “поместить” в построенное геометрическое место точек “эллипс” и этим точкам вставить анимацию. Прикрепляя некоторые точки основания стереометрической фигуры (многогранника) на эллипсе и вращая точки эллипса, получим эффект вращения стереометрической фигуры.
У программы ЖМ есть важное преимущество, это возможность создавать страницы и межстраничные ссылки между ними. Благодаря этому в ЖМ можно применить как электронный журнал, а это в свою очередь возможность создания учебно-методических комплексов. Работа в программе обеспечивает поддержку работы проектного типа, подразумевающего почти незаметный и плавный переход от несложных опытов и простых заданий к углубленному изучению явлений, вызвавших интерес. Кроме того, программная среда поддерживает и традиционную «задачную» форму. Особенно удачно реализуется в ней широкий спектр задач «на построение».
Используя задачу изучения и построения эллипса, необходимо объяснить школьникам, в каких областях науки используется "инструмент эллипс". Например, привести в пример астрономическую модель Солнечной системы. Можно ученикам предложить построить такую модель, используя программу «Живая Математика» или «GeoGebra». При этом необходимо, чтобы они самостоятельно выяснили глобальные параметры Солнечной системы, такие как массы планет, средние скорости вращения вокруг Солнца, расстояния от планет до Солнца. При составлении модели ученики, по возможности, должны учитывать экспериментальные значения этих параметров.
Анимационные возможности математических программ и задачи на развитие пространственного воображения
В качестве наглядного примера использования математических пакетов приведем комментарии по использованию анимационных возможностей этого пакета в ходе урока по теме «Вращение многогранников» в 11 классе по учебнику: И. Смирнова, В. Смирнов «Геометрия 10-11». – М.: Просвещение, 2008 [4]. Комментарии будут относиться как к созданию демонстрационного материала для визуализации геометрических разделов геометрии с помощью математических пакетов, так и к методической целесообразности по их применению. Рассматриваемый учебный материал также может быть использован на обобщающем уроке по геометрии в 11 классе по теме «Тела вращения», если изучение геометрии предполагается по учебникам Л. С. Атанасяна или А. В. Погорелова.
План-конспект фрагмента урока 11-го класса
Тема: Вращение многогранников.
Тип: Изучение нового материала.
Цели урока:
- образовательные:
1) закрепить понятия вращения в пространстве и фигуры вращения;
2) исследовать фигуру, получаемую при вращении прямой вокруг скрещивающейся с ней оси, ввести понятие гиперболоида вращения;
3) формирование умений и навыков исследования фигур, получаемых при вращении многогранников вокруг оси;
- воспитательные: воспитание познавательного интереса к предмету посредством включения в учебный процесс средств информационных технологий;
- развивающие: развитие пространственного воображения, логического мышления.
Оборудование: компьютер, мультимедийный проектор, математические программы: «Живая Математика» или «GeoGebra» или пакет символьной математики Maple.
Ход урока
Актуализация
Необходимо напомнить ученикам определения следующих понятий: поворот или вращение в пространстве; фигура вращения.
Затем ученикам предлагается решить ряд задач на пространственное вращение плоских фигур.
1) Изобразите фигуру вращения, полученную в результате вращения отрезка вокруг оси: а) перпендикулярной к нему и проходящей через один из его концов; б) пересекающей его в одном из его концов и не перпендикулярной к нему; в) пересекающей его во внутренней точке; г) параллельной ему.
2) Равносторонний треугольник вращается вокруг: а) высоты; б) стороны; в) прямой, параллельной высоте и проходящей: 1) через его вершину, 2) вне треугольника, 3) внутри треугольника. Изобразите в каждом случае получившееся тело.
3) Квадрат вращается вокруг: а) стороны; б) средней линии; в) прямой, параллельной стороне и проходящей вне квадрата; г) прямой, параллельной диагонали и проходящей через вершину. Изобразите в каждом случае полученное тело вращения.
4) Ромб вращается вокруг: а) стороны; б) прямой, перпендикулярной стороне и проходящей: 1) через его вершину, 2) вне его; в) прямой, перпендикулярной его диагонали и проходящей: 1) через его вершину, 2) вне его, 3) внутри его. Изобразите полученное тело вращения.
Эти задачи направлены на стимулирование пространственного мышления. В ходе их решения у учеников могут возникнуть трудности с созданием динамических образов фигур. Поэтому учитель должен обладать набором подсказок, которые могут облегчить мыслительный процесс ученика. Наиболее эффективными являются подсказки-визуализации, которые воспроизводят либо вращения начальных фигур вокруг заданных осей, либо предлагают сам процесс формирования искомой фигуры при вращении исходных элементов. Такие визуализации можно достаточно быстро создавать с помощью математических программ.
В качестве примера эффективности и наглядности программ такого типа рассмотрим подсказку для задачи г) пункта 3.
> restart: with(plottools):with(plots):
RECTAN:=polygon([[0,0,0],[10,0,0],[10,10,0],[0,10,0]], color=green, thickness=1):
axes:=PLOT3D(CURVES([[0,-10,0],[20,10,0]],COLOR(HUE,0.7),THICKNESS(1))):
fig:=PLOT3D(RECTAN):
f:=display([axes,fig]): RTS:=[seq(U[k],k=0..40)]:
for k from 0 to 40 do b:=k*0.25*Pi: U[k]:=rotate(f,b,[[0,-10,0],[20,10,0]]): end do:
RRT:=[seq(Y[j],j=0..40)]: for j from 0 to 40 do
RRS:=[seq(T[i],i=0..j)]: for i from 0 to j do b:=i*0.12*Pi:
T[i]:=rotate(f,b,[[0,-10,0],[20,10,0]]): end do:
Y[j]:=plots[display](RRS[],scaling=constrained,style=patch):end do:
display(RTS[],RRT[],insequence=true,scaling=constrained,style=patch);
Задается исходное расположение квадрата и оси вращения, а конечный результат на рис. 4.
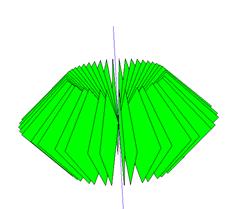
Сам процесс перехода от квадрата к рис. 4 анимирован. На первом этапе показывается только вращение квадрата. Если ученик не может описать фигуру, то учитель запускает процесс формирования фигуры. Причем программа не дает чертежа искомый фигуры, а предлагает трехмерную упрощенную модель этой фигуры, оставляя окончательный ответ все же за учеником.
Рис. 4. Динамический чертеж в программе “ Maple ” вращение квадрата вокруг оси
Выбор задач зависит от подготовленности учеников к решению задач на пространственное воображение. В заключение этой части урока учитель предлагает задачу, порождающую проблемную ситуацию:
Изобразите фигуру вращения, полученную в результате вращения отрезка вокруг оси скрещивающейся с ним.
Данная фигура ученикам не знакома. Учитель просит схематично ее изобразить. Задача требует высокого уровня пространственного мышления по манипулированию динамическими образами фигур. Поэтому, скорее всего, ответ на эту задачу придется дать самому учителю в ходе изложения материала урока.
Изложение нового материала
Разрешение проблемной ситуации предлагается провести в два этапа. На первом этапе осуществляется визуализация полученной при вращении фигуры средствами информационных технологий, используя одну из программ «Живая Математика», «GeoGebra» или «Maple».
Ученикам полученная фигура не знакома. Поэтому на втором этапе учитель исследует фигуру и вводит понятие гиперболоида вращения следующим образом.
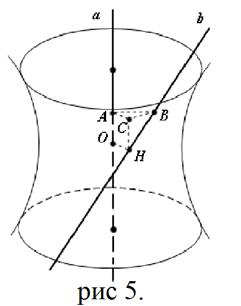 Пусть а и b – скрещивающиеся прямые, ОН – их общий перпендикуляр, обозначим эту длину через d. Она является наименьшей из длин отрезков, соединяющих точки прямых а и b. Поэтому при вращении точек прямой b вокруг оси a окружность наименьшего радиуса будет получаться при вращении точки Н (рис. 5).
Пусть а и b – скрещивающиеся прямые, ОН – их общий перпендикуляр, обозначим эту длину через d. Она является наименьшей из длин отрезков, соединяющих точки прямых а и b. Поэтому при вращении точек прямой b вокруг оси a окружность наименьшего радиуса будет получаться при вращении точки Н (рис. 5).
Рассмотрим произвольную точку B на прямой b, отличную от точки Н, и опустим из нее перпендикуляр АВ на прямую а. При вращении точка В описывает окружность, радиус которой равен АВ. Выразим этот радиус через d. Для этого через точку Н проведем прямую, параллельную а, и через точку А – прямую, параллельную ОН. Точку пересечения этих прямых обозначим С. Пусть расстояние АВ равно x, расстояние ОА равно y и угол ВНС равен ![]() . Треугольник АВС прямоугольный, катет АС равен d, катет ВС равен
. Треугольник АВС прямоугольный, катет АС равен d, катет ВС равен ![]() . Поэтому
. Поэтому ![]() .
.
Рис. 5. Динамический чертеж в программе “ Maple ”
Перенеся слагаемое, содержащее y, в левую часть равенства и разделив обе части полученного равенства на ![]() , получим уравнение
, получим уравнение ![]() , которое представляет собой уравнение гиперболы. В связи с этим фигура, получающаяся при вращении прямой b, скрещивающейся с осью вращения а, называется гиперболоидом вращения. (Решение приведено по учебнику И. Смирновой.)
, которое представляет собой уравнение гиперболы. В связи с этим фигура, получающаяся при вращении прямой b, скрещивающейся с осью вращения а, называется гиперболоидом вращения. (Решение приведено по учебнику И. Смирновой.)
Завершая комментарии к фрагменту урока, хотелось бы сказать, что сочетание традиционных методов обучения математике и информационных компьютерных технологий делает возможным представить такой тип взаимообусловленной деятельности учителя и учащихся, который направлен на развитие познавательной деятельности учащихся, на разрешение многих психолого-педагогических проблем, связанных с процессом обучения геометрических разделов математики.
Рецензенты:
Салехова Л.Л., доктор педагогических наук, доцент, зав. кафедрой математической лингвистики и информационных систем в филологии, Казанский (Приволжский) федеральный университет, г. Казань.
Широкова Е.А., доктор физико-математических наук, доцент, зав. кафедрой общей математики, Казанский (Приволжский) федеральный университет, г. Казань.



