Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Особенностью современного этапа развития системы высшего заочного образования является внедрение современных информационных образовательных интернет-технологий в организацию заочного обучения [6; 10]. При обучении с использованием дистанционных образовательных технологий (ДОТ) актуальными являются вопросы обеспечения качества образования и контроля знаний [3; 7; 9]. Одним из основных методов контроля знаний при дистанционном обучении является тестирование, эффективность результатов которого во многом определяется качеством тестовых заданий [4; 5].

В Томском политехническом университете последние 5 лет применяется форма заочного обучения с использованием ДОТ. В данной работе проведен кластерный анализ (аналогично [1; 2; 8]) результатов оценивания знаний по высшей математике (выборка ЭНИН4) в объеме 4-го семестра (дифференциальные уравнения, ряды, комплексный анализ, операционный метод) студентов Энергетического института. Рассмотрение проведено в системе 3-х переменных (рис. 1):

DT – разность моментов окончания и начала экзамена (в минутах),

ЭКЗ – набранные баллы за тест-экзамен в режиме online (из 40 – max),

ИДЗ – набранные баллы за 4 индивидуальных домашних задания (из 60 – max).

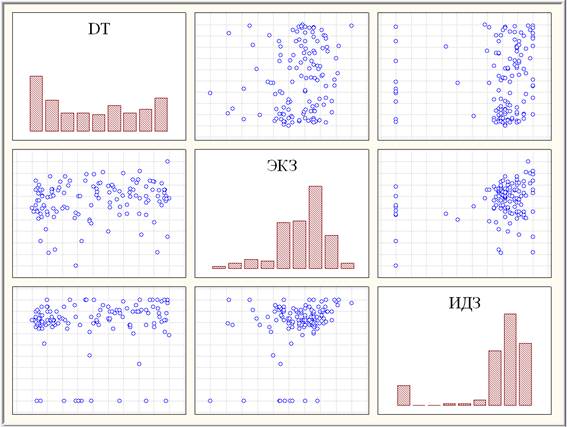
Рис. 1. Диаграммы рассеяния с гистограммами переменных выборки ЭНИН4

Из 130 участвовавших «неуд» (баллы ЭКЗ < 22) получили 25,4%, то есть каждый четвертый.

Особенностью полученных результатов является выделение многочисленной аномальной группы получивших положительный экзаменационный результат за минимальное время. Установленный рекорд составляет DT = 5 мин. Оказывается, что для пятой части (20%, рис. 2) сдавших для выполнения и оформления положительной экзаменационной работы по высшей математике достаточно было не более 20 минут из выделенных 3 часов.

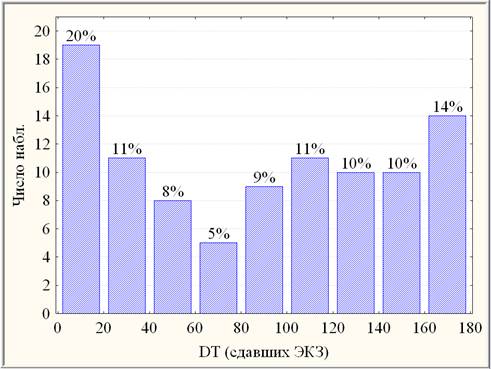
Рис. 2. Гистограмма DT по всем сдавшим ЭКЗ (97 студ.)

Выявленное аномальное обстоятельство лишний раз подчеркивает несовершенство стадии оценивания усвоенных студентом знаний при дистанционном обучении с использованием информационных образовательных интернет-технологий, создающее проблему идентификации студента: преподаватель должен быть уверен, что на другом конце телекоммуникационной цепочки находится именно тот человек, который претендует на получение не только определенных знаний, но и документа (диплома, свидетельства, удостоверения, сертификата) об освоении соответствующей образовательной программы [3; 6].

В данной работе на базе данных выборки ЭНИН4 проведен кластерный анализ результатов оценивания знаний по высшей математике в абсолютной и стандартизированной шкалах.

В рамках кластерного анализа методом K-средних, проводящим классификацию объектов по заданному количеству кластеров, получена 10-кластерная высококачественная модель результатов оценивания знаний по высшей математике (рис. 3), различающая 10 кластеров по совокупности показателей DT, ЭКЗ, ИДЗ высоко значимо (на уровне значимости р < 0,00005) согласно λ-критерию Уилкса.

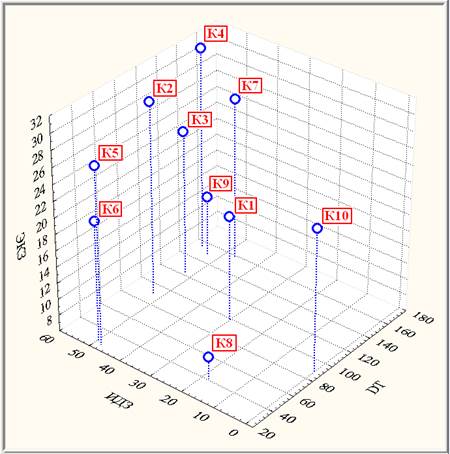
Рис. 3. Диаграмма рассеяния кластерных средних в системе {DT, ЭКЗ, ИДЗ}

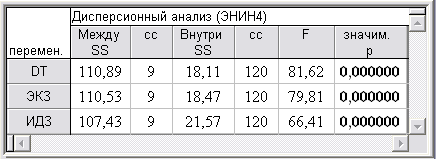
При этом согласно параметрическому F-критерию (табл. 1), ранговому критерию Краскела-Уоллиса и медианному тесту высоко значимо (на уровне значимости р < 0,00005) различаются 10 кластеров также по каждому показателю.

Таблица 1. Результаты дисперсионного анализа качества кластеризации в системе {DT, ЭКЗ, ИДЗ}

Рассчитанные средние значения показателей по каждому кластеру представлены в табл. 2 в абсолютной и стандартизированной шкалах.

Таблица 2. Кластерные средние m в системе {DT, ЭКЗ, ИДЗ}

Для наглядного оценивания значимости различий кластерных средних по показателям построены их линейные графики на рис. 4.

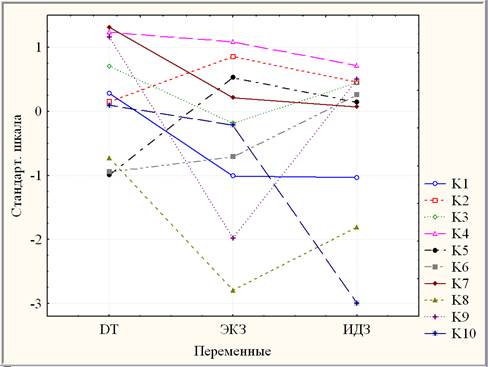
Рис. 4. Линейные графики кластерных средних в системе {DT, ЭКЗ, ИДЗ} по стандартизированной шкале

В рамках дисперсионного анализа можно выделить для каждого показателя однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) группы кластеров, расположенные в порядке убывания кластерных средних:

• DT: {К7, К4, К9}, {К3, К1}, {К1, К2, К10}, {К8, К6, К5}.
• ЭКЗ: {К4, К2}, {К5}, {К7}, {К3, К10}, {К6, К1}, {К9}, {К8}.
• ИДЗ: {К4, К9, К2, К3}, {К9, К2, К3, К6}, {К6, К5, К7}, {К1}, {К8}, {К10}.

Полученные результаты кластерного анализа (рис. 4 и табл. 2) позволяют провести качественную классификацию результатов оценивания знаний по высшей математике (выборка ЭНИН4) в номинальной шкале измерений (табл. 3), полагая при этом в качестве уровня «средний» - стандартизированный интервал (-0,5; +0,5) для показателей. Аномально высокие значения (> +1,5) определяют уровень «Лидер», а аномально низкие значения (< -1,5) определяют уровень «Аутсайдер». Промежуточные значения между средними и аномальными определяют уровень «выше среднего» и «ниже среднего» соответственно.

Таблица 3. Качественная классификация результатов оценивания знаний по высшей математике (выборка ЭНИН4)

Согласно рис. 4 и табл. 2-3, кластерная модель результатов оценивания знаний по высшей математике имеет спектральную структуру. Даже среди не сдавших экзамен (баллы ЭКЗ < 22) выделяются разные кластеры, значимо различающиеся по DT и ИДЗ: 8 условно допущенных (не сдавших все ИДЗ) имеют разное DT (mDT ≈ 40 для К8 и mDT ≈ 100 для К1) и 28 допущенных с разным DT (mDT ≈ 30 для К6 и mDT ≈ 150 для К9). Зона риска (mЭКЗ < 24) представлена двумя кластерами, разительно отличающимися по ИДЗ (mИДЗ = 0 для К10 и mИДЗ ≈ 53 для К3). Остальные 4 кластера допущенных и сдавших в разной степени успешно экзамен разнятся в большей степени значением DT: от «тугодумов» (mDT ≈ 160 для К7) до «легкодумов» (mDT ≈ 25 для К5). Одним из последних 29 (К5) является вышеотмеченный рекордсмен с DT = 5 мин. Связанную с этим аномальным обстоятельством проблему идентификации студента мы уже отметили.

Другой острой проблемой оценивания усвоенных студентом знаний при дистанционном обучении с использованием информационных образовательных интернет-технологий является чрезмерное увлечение автоматизацией итогового контроля знаний обучаемых в условиях несовершенства содержания и формы тестовых заданий: сдачи зачетов и экзаменов в форме компьютерного тестирования практически без участия преподавателя в оценивании полученных знаний.

Выводы

1. Получена 10-кластерная высококачественная модель результатов оценивания знаний по высшей математике, различающая высоко значимо 10 кластеров не только по совокупности показателей DT, ЭКЗ, ИДЗ, но и по каждому показателю.

2. В рамках дисперсионного анализа выделены для каждого показателя однородные (различающиеся незначимо) группы кластеров.

3. Проведена качественная классификацию результатов оценивания знаний по высшей математике в номинальной шкале измерений, детальным образом прописывающая структуру результатов оценивания усвоенных студентом знаний при дистанционном обучении с использованием информационных образовательных интернет-технологий.

4. Результаты подобной кластеризации результатов оценивания знаний могут быть учтены при внедрении современных информационных образовательных интернет-технологий в организацию заочного обучения для обеспечения качества образования и контроля знаний.

Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.

Рецензенты:

Трифонов Андрей Юрьевич, д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Арефьев Константин Петрович, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.