Введение. Решение задачи отбора сельскохозяйственных культур с помощью игровой модели было предложено в работах [1; 2; 6]. В статье [6] взаимодействие индивидуального фермера и гипотетической комбинации сил, определяющих рыночные цены, описано с помощью игры между двумя лицами с нулевой суммой. Рассмотренный там пример показал хорошую корреляцию фактического распределения культур на земле и игрового теоретического оптимального распределения. В то же время модель из [6] имеет ряд недостатков. Некоторые из них указаны непосредственно в работе [6], некоторые имеют более скрытый характер. К последним необходимо отнести характер предполагаемой в [6] платежной функции. Дело в том, что эта платежная функция основана на кривых эластичности спроса, в которых зависимость между объемом продукции и ценой является не совсем естественной. Неестественность, с нашей точки зрения, проявляется в скачкообразном поведении цены на продукцию при изменении объемов продукции, когда объемы имеют критический характер. Прежде всего, это относится к малым объемам. Но в условиях рынка цена на товары устанавливается спонтанно и свободно в результате совершения сделок множеством лиц с той и другой стороны (продавец - покупатель) и имеет равновесный устойчивый характер, несмотря на изменчивые условия формирования рыночной цены. Здесь можно сделать предположение, что при перенасыщении, или, наоборот, недонасыщении (дефиците) рынка товарами продавцы занимают выжидательную позицию и не спешат изменять цену товаров, так как и снижения, и повышения цены на товары могут привести к снижению выгоды, к невозможности покрыть издержки и даже, в крайнем случае, к банкротству. В конечном итоге продавцам придется привести цены в соответствие с насыщенностью рынка, но в первое время наступления такой ситуации продавцы не меняют цены. Здесь сказываются надежды на кратковременность сложившейся ситуации, повышение уровня доходов покупателей, ускорение реализации товаров. Продавцы в такой момент могут некоторое время заниматься поиском достоверной информации о длительности такого состояния рынка, использовать имеющиеся резервы или, наоборот, резервировать часть товаров, чтобы оживить спрос. Лишь только при отсутствии положительных сдвигов на рынке продавцы начинают обвальное снижение цен, стремясь вернуть себе часть средств и избежать банкротства.
Приведенные соображения говорят о необходимости изменения платежной функции из [6], что и является целью настоящей работы. Основные трудности, которые придется преодолеть на этом пути - это потеря выпуклости платежной функции. В связи с этим в работе отдельно для рассматриваемого случая установлены некоторые известные факты теории игр, необходимые для решения поставленной задачи.
Постановка задачи. Воспользуемся положениями из [6]. Будем считать, что на рынке цена произведенного однотипного продукта является функцией от его количества, т.е.
![]() , (1)
, (1)
где через ![]() обозначим цену единицы веса зерна типа
обозначим цену единицы веса зерна типа ![]() , а через
, а через ![]() - общее количество зерна
- общее количество зерна ![]() - го типа на рынке.
- го типа на рынке.
Будем также полагать, что хозяйства достаточно малы. Вследствие этого, не слишком огрубляя модель, можно принять, что
![]() , (2)
, (2)
где ![]() - средняя урожайность зерна
- средняя урожайность зерна ![]() -го типа,
-го типа, ![]() - общая площадь полей всех производителей, а
- общая площадь полей всех производителей, а ![]() - доля этой площади, на которой посеяно зерно
- доля этой площади, на которой посеяно зерно ![]() -го типа.
-го типа.
Пусть арендатор земли площади ![]() может посеять
может посеять ![]() типов зерна. Обозначив через
типов зерна. Обозначив через ![]() - урожайность зерна типа
- урожайность зерна типа ![]() , а через
, а через ![]() - долю площади, засеянную этим зерном, выразим цену полученного арендатором продукта формулой
- долю площади, засеянную этим зерном, выразим цену полученного арендатором продукта формулой
![]() . (3)
. (3)
Тогда, подставляя формулы (1) и (2) в выражение (3), получим
![]() . (4)
. (4)
Обозначив через игрока I - рынок, а через игрока II отдельно арендатора, мы приходим к антагонистической игре, в которой стратегиями игрока I будут векторы ![]() ; стратегиями игрока II - векторы
; стратегиями игрока II - векторы ![]() ; функция выигрыша задается формулой (4).
; функция выигрыша задается формулой (4).
Очевидно, что чем больше произведено зерна, тем меньше его рыночная цена. Будем считать, что каждая из функций ![]() имеет вид
имеет вид ![]() ; коэффициенты
; коэффициенты ![]() и
и ![]() найдем статистическим методом, используя регрессионные модели. Заметим, что по сравнению с [6] здесь зависимость цены от доли засеваемой площади выбрана так, что при малых долях цена равна ненулевому конечному числу, что больше соответствует реальности (в [6] при стремлении площади к нулю цена неограниченно возрастает).
найдем статистическим методом, используя регрессионные модели. Заметим, что по сравнению с [6] здесь зависимость цены от доли засеваемой площади выбрана так, что при малых долях цена равна ненулевому конечному числу, что больше соответствует реальности (в [6] при стремлении площади к нулю цена неограниченно возрастает).
После подстановки выражения для ![]() в формулу (4), получим
в формулу (4), получим
![]() . (5)
. (5)
В этом случае функция выигрыша (5) является линейной по стратегии игрока II и не является выпуклой относительно стратегии игрока I. Следовательно, использовать результаты, полученные для выпуклых игр [3-5], нельзя. В следующем пункте работы получим некоторые факты, необходимые для построения решения в нашем случае.
Решение задачи. Рассмотрим непрерывные антагонистические игры [1-4], т.е. системы вида
![]() ,
,
где ![]() множества стратегий игроков I и II, а
множества стратегий игроков I и II, а ![]() :
:![]() - непрерывная функция выигрыша игрока I (проигрыша игрока II), вычисляемая по (5). Как обычно, смешанными стратегиями игроков в
- непрерывная функция выигрыша игрока I (проигрыша игрока II), вычисляемая по (5). Как обычно, смешанными стратегиями игроков в ![]() считаются вероятностные распределения на множествах их чистых стратегий
считаются вероятностные распределения на множествах их чистых стратегий ![]() и
и ![]() , которые являются стохастически независимыми. Множество всех смешанных стратегий игроков мы обозначим через
, которые являются стохастически независимыми. Множество всех смешанных стратегий игроков мы обозначим через ![]() соответственно.
соответственно.
Пусть ![]() и
и ![]() смешанные стратегии соответственно игроков I и II в игре
смешанные стратегии соответственно игроков I и II в игре ![]() . Выигрыш
. Выигрыш ![]() представляет собой выражение
представляет собой выражение
![]() ,
,
причем интегралы в этих равенствах понимаются в смысле Стилтьеса.
Для оптимальных смешанных стратегий ![]() ,
, ![]() , и
, и ![]() ,
, ![]() , с любыми смешанными стратегиями
, с любыми смешанными стратегиями ![]() и
и ![]() соответственно игроков I и II должны выполняться неравенства
соответственно игроков I и II должны выполняться неравенства
![]() . (6)
. (6)
Известно [1; 3; 4], что решение приведенной игры существует при достаточно общих предположениях относительно множеств ![]() и функций
и функций ![]() . Будем строить решение по схеме поиска оптимальных стратегий для выпуклой платежной функции [4], [5]. Принципиальным моментом на этом пути является наличие чистой стратегии
. Будем строить решение по схеме поиска оптимальных стратегий для выпуклой платежной функции [4], [5]. Принципиальным моментом на этом пути является наличие чистой стратегии ![]() первого игрока (для второго игрока это очевидно), что мы сейчас и установим.
первого игрока (для второго игрока это очевидно), что мы сейчас и установим.
Заметим, что если определенная на множестве ![]() достаточно гладкая функция
достаточно гладкая функция ![]() достигает своего наибольшего значения в точке
достигает своего наибольшего значения в точке ![]() из внутренности
из внутренности ![]() , то очевидно существует максимальный n-мерный куб
, то очевидно существует максимальный n-мерный куб ![]() , лежащий в
, лежащий в ![]() с центром в точке
с центром в точке ![]() , такой, что функция
, такой, что функция ![]() является вогнутой в
является вогнутой в ![]() . Этот n-мерный куб будем называть кубом вогнутости функции
. Этот n-мерный куб будем называть кубом вогнутости функции ![]() . Итак, куб вогнутости
. Итак, куб вогнутости ![]() всегда для названной функции не пуст. В вырожденном случае считаем
всегда для названной функции не пуст. В вырожденном случае считаем ![]() . В случае, если точка
. В случае, если точка ![]() находится на границе множества
находится на границе множества ![]() , то куб
, то куб ![]() с названными выше свойствами и вершиной в токе оптимальности также будем называть кубом вогнутости функции
с названными выше свойствами и вершиной в токе оптимальности также будем называть кубом вогнутости функции ![]() . Имеет место следующая теорема.
. Имеет место следующая теорема.
Теорема. В игре ![]() с платежной функцией из (5) игрок I имеет чистую оптимальную стратегию.
с платежной функцией из (5) игрок I имеет чистую оптимальную стратегию.
Доказательство. Рассмотрим игру ![]() с функцией выигрыша
с функцией выигрыша ![]() , где
, где ![]() ,
, ![]() и
и ![]() ,
, ![]() .
.
Пусть ![]() - цена игры
- цена игры ![]() ,
, ![]() - одна из оптимальных стратегий игрока I, а
- одна из оптимальных стратегий игрока I, а ![]() - игрока II.
- игрока II.
Обозначим через
![]() .
.
Очевидно, что начало координат является максимальной для функции ![]() точкой. Пусть
точкой. Пусть ![]() - куб вогнутости с вершиной в этой точке, находящийся в неотрицательном ортанте. Покажем, что
- куб вогнутости с вершиной в этой точке, находящийся в неотрицательном ортанте. Покажем, что ![]() . Для этого достаточно установить, что
. Для этого достаточно установить, что
![]() ,
, ![]() . (7)
. (7)
Рассмотрим функцию
![]() ,
, ![]() .
.
Эта функция является непрерывной на ![]() и в силу характера платежной функции принимает свое наибольшее значение только в каких-то точках множества
и в силу характера платежной функции принимает свое наибольшее значение только в каких-то точках множества ![]() . Поэтому вне
. Поэтому вне ![]() для достаточно малого положительного
для достаточно малого положительного ![]() можно считать выполненным неравенство
можно считать выполненным неравенство ![]() , где
, где ![]() .
.
Отсюда следует, что
![]() ,
,
где ![]() .
.
Как известно [1], ![]() , и, следовательно,
, и, следовательно, ![]() .
.
Поскольку здесь ![]() , то выражение
, то выражение ![]() не может быть положительным. С другой стороны, в силу вероятностного смысла оно не может быть отрицательным. Таким образом, имеет место равенство
не может быть положительным. С другой стороны, в силу вероятностного смысла оно не может быть отрицательным. Таким образом, имеет место равенство ![]() , которое из-за произвольности
, которое из-за произвольности ![]() доказывает справедливость (7). Итак,
доказывает справедливость (7). Итак, ![]() и, более того,
и, более того,
![]() . (8)
. (8)
Отсюда следует, что
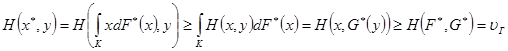
для любого ![]() .
.
Следовательно [1], ![]() является оптимальной стратегией игрока I. Теорема доказана.
является оптимальной стратегией игрока I. Теорема доказана.
Итак, каждый из игроков имеет оптимальные чистые стратегии.
Пример. Решим эту задачу для случая ![]() . Найдем оптимальные стратегии игрока I (рынка) и игрока II (арендатора), используя данные по производству кукурузы, пшеницы и овса в США на площади
. Найдем оптимальные стратегии игрока I (рынка) и игрока II (арендатора), используя данные по производству кукурузы, пшеницы и овса в США на площади ![]() акров за 1958 год [6], которые приведены в таблице 1.
акров за 1958 год [6], которые приведены в таблице 1.
Таблица 1 - Статистические данные о сельскохозяйственных культурах
|
Вид зерна |
Кукуруза |
Пшеница |
Овес |
|
Показатели |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После подстановки величин ![]() в формулу (5) получим
в формулу (5) получим
![]() . (9)
. (9)
Тогда
![]() .
.
Отсюда численным методом, используя программную среду Delphi 7.0, находим вектор ![]() и цену игры
и цену игры ![]() долларов на акр.
долларов на акр.
Для вычисления оптимальных стратегий II игрока найдем частные производные функции
![]()
по аргументам ![]() , принимая во внимание, что
, принимая во внимание, что ![]() и
и ![]() , а затем приравняем их к нулю. В результате придем к системе уравнений
, а затем приравняем их к нулю. В результате придем к системе уравнений
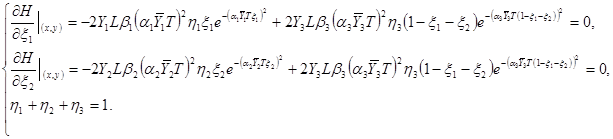
решением которой будет вектор ![]() .
.
Решим теперь задачу в предположении, что каждая из функций (1) имеет вид: ![]() (именно в таком виде обычно берутся функции
(именно в таком виде обычно берутся функции ![]() [6]). Функция выигрыша
[6]). Функция выигрыша
![]() (10)
(10)
является линейной по стратегии игрока I и выпуклой относительно стратегии игрока II.
Решив задачу для наших данных, получим цену игры ![]() долларов на акр.
долларов на акр.
Выводы. Использование функции выигрыша в виде (5) в известной задаче о рациональной схеме посевов различных сельскохозяйственных культур приводит к лучшим результатам, чем применение выпуклой функции выигрыша. С экономической точки зрения такая функция лучше отражает реальные рыночные отношения и, самое главное, является более выгодной, т.е. позволяет получить более высокую цену игры.
Рецензенты:
Долгова Елена Владимировна, доктор экономических наук, профессор кафедры «Информационные технологии и автоматизированные системы» Пермского национального исследовательского университета, г. Пермь.
Елохова Ирина Владимировна, доктор экономических наук, профессор, заведующий кафедрой «Управление финансами» Пермского национального исследовательского университета, г. Пермь.



