Введение
Непрерывный спекулятивный рост цен на активы на финансовых рынках, приводящий к отклонению текущей цены актива от ее фундаментального уровня и, как следствие, возникновению пузырей во многих странах, вызывает все большую озабоченность среди исследователей, экспертов и финансовых регуляторов. В результате в последнее время все большее количество ученых работает в направлении разработки эффективных методов прогнозирования, идентификации, измерения и датирования пузырей.
Пузырь - это значительное отклонение рыночной стоимости актива от его справедливой стоимости. Справедливая стоимость - это стоимость актива, рассчитанная из условия, что нам известны доходы, генерируемые этим активом в будущем, а также какому риску они подвержены.
1. Методы идентификации и измерения пузырей
Все методы делятся на следующие группы в зависимости от того, как они справляются с принципиальной проблемой идентификации спекулятивных пузырей (рисунок 1).
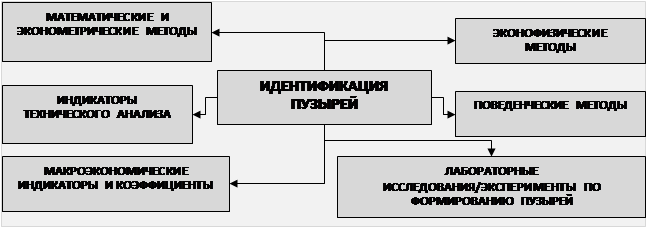
Рисунок 1. Методы идентификации и измерения параметров пузырей.
Источник: Н.А. Станик, В.А. Иванюк, Е.В. Маевский, В.Ю. Попов, А.Б. Шаповал. Идентификация периодов спекулятивного роста на фондовых рынках : монография. – М., 2012.
Основные методы обнаружения пузырей исследуют изучаемое нами явление через призму какой-либо одной науки.
Больше всего исследований принадлежит экономистам. Среди последних работ следует отметить исследования Роберта Шиллера (Robert Schiller), Пола Кругмана (Paul Krugman), Джозефа Стиглица (Josef Stieglitz) и многих других.
К проблематике финансовых пузырей обращались психологи и социологи, здесь можно назвать работы Чарльза Маккея, Гюстава ле Бона (Gustave Le Bon), Габриэля Тарда (Gabriel Tarde), Бернарда Баруха (Bernand Baruch), Мориса Кларка (Moris Clark), Джорджа Катона (George Katona), Сержа Московичи (Serge Moscovichi).
Очень активно, особенно в последнее время, проблемой пузырей и кризисов на финансовых рынках занимаются физики и математики. В частности, широкую известность получили работы швейцарского физика-сейсмолога Дидье Сорнета, применившего теорию катастроф к анализу финансовых рынков. Разделяя точку зрения о необходимости междисциплинарного подхода, можно, тем не менее, отметить спорность идеи о возможности создать единую теорию финансовых пузырей. Это слишком сложный феномен.
2. Характеристика основных групп и видов пузырей
В настоящее время существуют две группы пузырей: рациональные и иррациональные. В зависимости от условий образования пузырей и их дальнейшей динамики можно выделить следующие виды пузырей.
Спекулятивные пузыри (traditional, nonrational bubbles). Анализ спекулятивных пузырей дан в исследованиях Гамильтона (Hamilton,1986), где рассматриваются самореализующиеся спекулятивные пузыри; Шиллера (Shiller, 2000), Сигела (Siegel, 2003), где предлагается функциональное определение пузырей.
Актив приобретается потому, что инвестор ожидает дальнейшего роста цен, но его ожидания не основаны на объективных изменениях в фундаментальных показателях. Таким образом, первоначальное повышение стоимости актива приводит к дальнейшему росту цен. Возможным объяснением данной ситуации является гипотеза адаптивных ожиданий и зависимость между степенью уверенности инвесторов в продолжении роста и непосредственной динамикой цены. Ограничением для изучения данного вида пузырей является невозможность определения вероятности продолжения роста цены.
Рациональные пузыри. Рациональный пузырь – это разница между рыночной ценой и ценой, которая основывается на фундаментальных составляющих.
Гипотеза о рациональных ожиданиях (ГРО) экономических агентов предполагает, что при прогнозировании будущих экономических показателей агенты не делают систематических ошибок. А именно: прогнозное значение показателя, который попытается предсказать агент, в среднем будет равно фактическому. Вместе с тем предполагается, что для составления своего мнения относительно перспектив на будущее репрезентативные агенты используют всю доступную и имеющую отношение к принятию решения информацию. В случае отсутствия на рынке неопределенности и доступности полной информации ГРО сводится к гипотезе совершенного предвидения.
Таким образом, ГРО позволяет объяснить, что такое фундаментальная цена, определить содержание рационального пузыря, который может присутствовать в цене актива и отклонять цену от фундаментальной.
Одним из первых исследований по этой тематике является работа Бланчарда и Уотсона (Blanchard, Watson), в которой авторы показали, что возможны рациональные отклонения наблюдаемой цены активов в течение длительного интервала времени от фундаментально обоснованного уровня. Из современных интерпретаций рационального пузыря наибольшую известность получила работа Гуркайнака (Gurkaynak), в которой дается следующая дефиниция пузыря. Согласно ей, «цена акции содержит рациональный пузырь, если инвесторы желают платить за нее больше, чем, как они знают, она стоит исходя из величины дисконтированного потока дивидендов. Они рассчитывают, что смогут продать ее по более высокой цене в будущем, делая текущую более высокую цену равновесной ценой». Причем такая цена по-прежнему остается рациональной, а арбитражные возможности отсутствуют. Важно отметить, что рациональность в данном случае заключается в том, что инвесторы по предположению знают о наличии пузыря в цене актива. Рациональный инвестор приобретает такой актив, поскольку уверен в своей способности реализовать его до начала резкого снижения котировок, а повышение стоимости актива является достаточной компенсацией за рост уровня неопределенности.
Потенциал для рациональных спекулятивных пузырей существует в большинстве моделей ценообразования, в которых равновесная цена в текущем периоде зависит от ожиданий о будущих изменениях цены актива. В этих моделях такие пузыри могут появляться, если ожидания рациональны, и текущая равновесная цена зависит непосредственно от ожидаемых темпов роста актива.
Эти модели рациональных спекулятивных пузырей неопределенны. Другими словами, они имеют бесконечное множество равновесных решений. Неопределенность возникает, потому что модели ценообразования с такой структурой существенным образом обладают только одним условием удержания рынка в равновесном состоянии и соблюдается рациональность ожиданий, принимая во внимание, что решение модели диктует определение для двух эндогенных (внутренних) переменных – текущей равновесной цены актива и скорости ее изменения – в каждом периоде. Таким образом, в этих моделях может существовать множество решений цены актива или траекторий, в которых только одно решение соответствует основным экономическим принципам; другие траектории будут все содержать пузыри цены актива.
Рациональные детерминированные пузыри (Rational deterministic (ever-expanding) bubble.
В самой простой форме рациональный пузырь может следовать за детерминированным промежутком времени, отклоняясь от фундаментальных значений и экспоненциально возрастая.
Пузырь определяется неслучайными факторами: размером в предыдущий период и ставкой дисконтирования r. В связи с вышеизложенным детерминированный или разбухающий (ever-expanding) пузырь ![]() будет равен:
будет равен:
![]() . (1)
. (1)
Такие пузыри, как и фундаментальная цена акции, будут расти бесконечно со скоростью (1+r). В соответствии с данным уравнением цена актива может отклониться от своей фундаментальной стоимости, тем самым образуя взрывоопасный пузырь.
Лопающиеся пузыри (collapsing bubble)
Характерной чертой лопающихся пузырей является существование вероятности «сдутия» или «схлопывания» пузыря до нулевого (или ненулевого, сколь угодно малого) уровня.
Наиболее общая и простая формула лопающегося пузыря имеет следующий вид:
![]() (2)
(2)
![]() (3)
(3)
Данные выражения имеют следующую интерпретацию: инвесторы понимают, что пузырь рано или поздно лопнет, однако они получают более высокую доходность (![]() ) до тех пор, пока сверхвысокая доходность позволяет компенсировать риски неизбежного коллапса цен.
) до тех пор, пока сверхвысокая доходность позволяет компенсировать риски неизбежного коллапса цен.
Непрерывно возобновляющиеся пузыри (continuously regenerating bubble)
Такие пузыри в каждом периоде времени могут появляться заново в соответствии с процессом «белого шума», который их определяет:
![]() (4)
(4)
где ![]() - «белый шум».
- «белый шум».
Рациональные стохастические пузыри (rational stochastic bubble)
О. Бланчард и М. Уотсон предложили более реалистичную модель пузырей, часто называемую рациональные стохастические пузыри или модель пузырей рациональных ожиданий. Характерной чертой данной модели является то, что наблюдаемые цены могут значительно отклоняться (расти) от фундаментальных цен, образуя пузырь, в течение длительных интервалов времени, перед тем как внезапно лопнуть.
Данный стохастический процесс можно выразить следующим уравнением:
![]() (5)
(5)
![]()
где инновация пузыря ![]() удовлетворяет
удовлетворяет ![]()
Согласно данной формулировке существует вероятность ![]() , что пузырь сохранится до следующего периода, и вероятность (1-
, что пузырь сохранится до следующего периода, и вероятность (1-![]() ), что пузырь лопнет в текущем периоде. Если пузырь лопается, то наблюдаемая цена актива станет равна её внутренней стоимости. Термин «инновация» e означает, что пузырь может самовосстанавливаться после краха; таким образом, стохастический пузырь может, лопнув, сразу же возникнуть снова, и так беспрерывно.
), что пузырь лопнет в текущем периоде. Если пузырь лопается, то наблюдаемая цена актива станет равна её внутренней стоимости. Термин «инновация» e означает, что пузырь может самовосстанавливаться после краха; таким образом, стохастический пузырь может, лопнув, сразу же возникнуть снова, и так беспрерывно.
«Комиссионные» пузыри (пузыри «накрутки») (churning bubble). Возникают из-за наличия асимметрии информации между клиентами и портфельными менеджерами, что провоцирует менеджера проводить большое число спекулятивных сделок для максимизации комиссионного вознаграждения, зависящего от числа сделок. В данном случае цены могут не отражать фундаментальные показатели компании-эмитента.
По мнению Ф. Аллена и Г. Гортона, пузыри «накрутки» обусловлены изъянами схем стимулирования инвестиционных управляющих, которые и провоцируют их включаться в спекулятивную игру. Наличие опциона колл в компенсационных схемах инвестиционных управляющих (побуждающее их увеличивать прибыль, а не сокращать издержки) означает, что они могут желать приобрести акции, если существует некоторая перспектива прироста капитала, хотя им известно наверняка, что через какое-то время их стоимость упадет ниже текущего уровня.
Иррациональные пузыри (Irrational Bubble)
Пузыри, которые не основываются на предположении о рациональности ожиданий, носят название иррациональных. Так, Шиллер (Shiller, 2003) предлагает два подхода к иррациональному поведению экономических агентов: модель обратной связи (feedback model) и модель «noise traders».
Модель обратной связи
В рамках данной модели предполагается, что существуют инвесторы, которые уже приобрели активы в период появления и формирования пузыря на рынке, причем прибыльность операций с активами очень высока. Данные инвесторы, информируя других участников торгов о прибыльности операций, таким образом, привлекают дополнительные средства для вложений в активы. Очевидна схожесть такого пузыря с финансовой пирамидой (Ponzi scheme), когда наиболее информированные и опытные инвесторы получают больший доход, формируемый за счет средств остальных привлекаемых инвесторов.
Модель «noise traders»
Согласно данной модели предполагается, что в противовес профессиональным инвесторам существуют агенты (иррациональные инвесторы), торгующие по причинам и правилам, не объясняемым стандартной моделью. Поведение таких агентов может вызывать дисбалансы на фондовом рынке.
В целом работы, исследующие поведение индивидов на финансовых рынках и модели образования пузырей и крахов, можно разделить на две группы.
Первая группа моделей пузырей и фондовых крахов изучает причины значительных изменений цен на ценные бумаги в случае небольших изменений в окружающей среде, которые приводят к появлению существенной информации, выявляемой частично информированными инвесторами. Данный класс включает модели Abreu & Brunnermeier, Caplin & Leahy, Hong & Stein, Kraus & Smith, Lee, Romer, Zeira.
Вторая группа моделей объясняет фондовые крахи ошибочными действиями рациональных инвесторов, которые реагируют на сброс ценных бумаг со стороны иррациональных инвесторов. Данные модели основаны на существовании трейдеров, использующих схемы автоматического страхования портфеля ценных бумаг с помощью компьютеров (program trading), которые механически продают ценные бумаги, когда цены начинают снижаться. Данная группа включает модели Gennotte & Leland, Grossman, Jacklin, Kleidon & Pfleiderer.
Рецензенты:
Терелянский Павел Васильевич, д.э.н., профессор, зав. кафедрой «Информационные системы в экономике» ВолгГТУ, г. Волгоград.
Гущина Елена Геннадьевна, д.э.н., профессор кафедры «Мировая экономика и экономическая теория», ВолгГТУ, г. Волгоград.



