Введение
Оценка фактического состояния силового трансформатора по результатам диагностических измерений является на сегодняшний день сложной и актуальной задачей. Одной из важных задач диагностики является оценка механического состояния обмоток трансформатора. При токах короткого замыкания теряется электродинамическая стойкость – происходят механические повреждения. Это осевые и радиальные остаточные деформации, скручивание и раскручивание обмоток. Одним из альтернативных методов диагностики является метод зондирующего импульса напряжения длительностью порядка микро-, наносекунд, который подается на обмотки трансформатора. При соответствующем выборе формы импульса можно получить частотный спектр зондируемого сигнала с богатым высокочастотным наполнением. Высокочастотные компоненты зондирующего импульса возбуждают токи смещения, которые, протекая через распределенные емкости трансформатора, вносят свой уникальный вклад в формирование спектра выходного сигнала. При наличии дефектов, обусловленных смещением или механической деформацией, в обмотках трансформатора меняются величины распределенных емкостей, что неизбежно скажется на спектре выходного сигнала. Следовательно, сравнивая эталонный спектр выходного сигнала трансформатора без деформаций со спектром выходного сигнала трансформатора с дефектом, можно обнаружить наличие деформаций [1; 6]. Таким образом, дефекты, обусловленные удлинением и поперечным расширением обмотки трансформатора, изменяют величины распределенных емкостей трансформатора.
Цель исследования
Поэтому целью данной работы является вывод основных соотношений для оценки поперечных и продольных деформаций проводов обмотки трансформатора, вызванных током короткого замыкания.
Вывод основных соотношений
Приведем необходимые соотношения для расчета продольной и поперечной деформаций одного витка обмотки трансформатора. Эти соотношения полезны для оценки продольного удлинения и поперечного расширения одного витка обмотки при известном токе проводника. Затем приведем расчет поля распределения пространственной деформации проводников в уединенной обмотке.
Изменение объема тела характеризуется компонентами вектора смещения 
которые определяются тензором деформации 
[4]:
(1)
Здесь по немым индексам суммирования будем считать, что отсутствуют деформации вращения. Тензор деформации можно привести к главным осям. Это означает, что оси координат ориентированы таким образом, что тензор имеет только диагональные элементы:
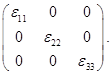(2)
Диагональные элементы называются главными деформациями и описывают растяжение или сжатие элемента объема в направлении главных осей. След тензора 
– сумма диагональных элементов, есть относительное удлинение объема, которое можно получить с учетом выражения (1) [4]:
(3)
Между компонентами тензора существуетсвязь:
, (4)
здесь 
– элемент тензора напряжений вдоль оси 
, 
– модуль Юнга (модуль растяжения),
, (5)
здесь 
– коэффициент Пуассона (отношение поперечного сжатия к продольному расширению).
Определим деформации кольцевого медного провода с магнитной проницаемостью 
под действием магнитного поля протекающего по нему тока. Пусть 
– механическое напряжение, действующее вдоль оси провода, а 
– механическое напряжение, действующее поперек оси. Определим эти напряжения.
Сила 
, действующая вдоль оси проводника, есть поперечное напряжение 
умноженное на площадь поперечного сечения проводника, т. е. 
, учитывая изменение энергии магнитного поля проводника вдоль его оси, можно записать:
(6)
где 
– длина проводника, 
– индуктивность кольца, зависящая от геометрических размеров проводника, 
– ток проводника.
Сила 
, действующая поперек оси проводника, есть продольное напряжение 
умноженное на площадь поверхности проводника, т. е. 
, учитывая изменение энергии магнитного поля вдоль радиуса 
, можно записать:
а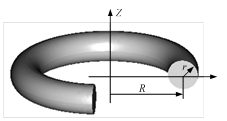 
б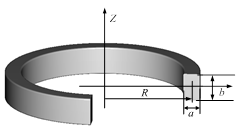 
Рис. 1. Геометрические параметры витков обмотки: а) круглого сечения, б) прямоугольного сечения
. (7)
Уравнения (6) и (7) позволяют определить связь между продольным и поперечным напряжениями с продольной и поперечной силами:
. (8)
Запишем выражение для индуктивности проводника в виде кольца с круглым поперечным сечением [3] (рис. 1а):
, (9)
используя соотношения (8) и (9), получим:
, 
И, наконец, используя выражение для относительного смещения и уравнения связи (4), (5), получим относительное удлинение проводника круглого сечения:
.
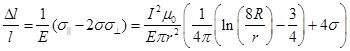Проделаем аналогичные операции для кольца с прямоугольным поперечным сечением, имеющего следующую формулу для индуктивности [3] (рис. 1б) и для погонных индуктивностей:
Находим напряжения, действующие вдоль оси и перпендикулярно к ней:
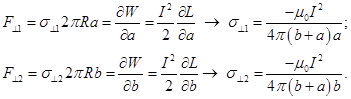
Находим относительное удлинение кольца:
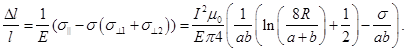
Для того чтобы подсчитать изменение емкости кольцевого проводника круглого сечения, нужно использовать известную формулу расчета емкости [2]:
При пренебрежении температурной деформацией изменение емкости будет определяться выражением:
.
Здесь 
Таким образом, получены полезные соотношения, позволяющие оценить продольные и поперечные деформации одного витка обмотки и изменение емкости витка.
Методика исследования
Для получения пространственного распределения деформаций обмотки трансформатора нужно учитывать не только индуктивность одного витка, но и взаимную индуктивность всех витков. Пространственное распределение деформирующих сил в электромагнитном поле называют пондеромоторными силами [2; 4]. Для правильной оценки деформации проводников необходимо рассчитать распределение пондеромоторных сил. Для этого нужно использовать систему уравнений Максвелла и тензор натяжения Максвелла [3; 6]. Используя уравнения Максвелла, рассчитаем векторный магнитный потенциал 
, а затем распределения магнитной напряженности 
поля, вызванного током проводников:
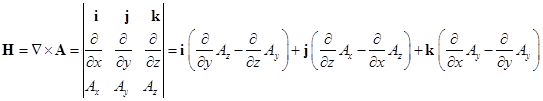
Здесь 
магнитная проницаемость, 
– плотность тока проводника, 
– векторный магнитный потенциал.
Решив уравнение Пуассона, получим векторный магнитный потенциал A с последующим определением напряженности магнитного поля H. Далее для определения распределения тензора деформаций Максвелла используем соотношение [4; 5]:
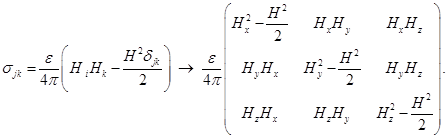
Здесь 
– диэлектрическая проницаемость 
– компонента магнитного поля, 
– элементы тензора механических напряжений, 
– символ Кронекера.
Интегрирование тензора механического напряжения по поверхности проводников обмотки даст нам распределение поверхностных сил деформаций обмотки [2; 4]:
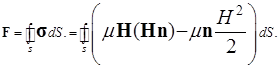
Моделирование в среде COMSOL Multiphysics
В качестве примера приведем модельную задачу расчета эпюры распределений поверхностных сил в магнитном поле проводников обмотки c использованием метода конечных элементов. Для реализации метода конечных элементов был использован пакет COMSOL Multiphysics. Рассматривались две отдельные обмотки. Одна намотана медным проводом диаметром 
с шагом 
, количество витков 
, внутренний диаметр 
, внешний диаметр 
, длина медного кабеля 
, основа – полихлорвиниловый цилиндр. Другая обмотка намотана медной шиной с размерами 
, количество витков 
, внутренний диаметр 
, внешний диаметр 
, длина медного кабеля 
, основа – винипластовый цилиндр.
На рис. 2 приведены две обмотки по пять проводников с различным поперечным сечением. В трех проводниках, находящихся в центре обмотки, произошло короткое замыкание, вследствие чего эти проводники имеют повышенное значение тока. В модели рассматривался ток короткого замыкания, превышающий ток нормального режима в 3 раза. На данном рисунке приведено распределение векторного магнитного потенциала A, распределение поверхностных сил F и результирующие силы, действующие на отдельный проводник. Для наглядности распределение поверхностных сил преувеличено. В месте короткого замыкания проводников возбуждается сильное магнитное поле, обусловленное высоким током. Здесь приведены только левые части аксиально-симметричных картин.
а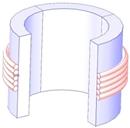
б 
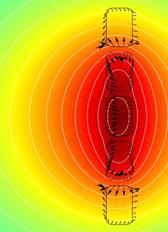
Рис. 2. Распределение поверхностных сил деформации проводников обмотки. Результирующие силы, действующие на уединенные проводники: а) круглого сечения; б) прямоугольного сечения
Огибающая кривая эпюр поверхностных сил повторяет форму деформированного проводника. Результирующие вектора показывают направления смещения проводников.
Заключение
В работе получены полезные соотношения, позволяющие оценить продольные и поперечные деформации проводников обмотки, вызванные током короткого замыкания. Получены формулы, позволяющие оценить изменение емкости круглой обмотки при деформации обмотки. Приведен расчет деформаций, демонстрирующий распределение пондеромоторных сил на поверхности проводников обмотки, показаны результирующие вектора действующих на уединенные витки сил при токах короткого замыкания.
Рецензенты:
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Курец В.И., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.