Введение
Существует множество различных видов комбинаторных задач, для каждого из которых имеются свои тривиальные методы решения. Универсальным считается метод полного перебора, однако при большом количестве оперируемых данных [1] возникает проблема в вычислительных мощностях, что делает его абсолютно неэффективным. Поэтому для отдельных типов комбинаторных задач разрабатываются свои уникальные быстрые алгоритмы поиска решения, находящие не всегда наилучший ответ, но всегда предлагающие эффективное решение задачи.
Цель исследования
Одним из таких методов является генетический алгоритм (ГА), который постепенно улучшает некоторое текущее приближенное решение путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Однако для решения различных видов комбинаторных задач необходима своя настройка параметров генетического алгоритма. Для оценки эффективности его работы авторами рассматриваются следующие задачи: задача коммивояжера и задача поиска кратчайшего пути в графе.
Материалы и методы исследования
Рассмотрим основные понятия теории генетических алгоритмов применительно к указанным задачам. Популяция представляет собой определенное количество отдельных индивидов (хромосом), каждый из которых несет в себе некоторое решение задачи [2, 8]. В рассмотренных примерах это последовательность прохождения точек, иначе маршрут. Инициализация начальной популяции происходит случайным образом путем генерации числовых последовательностей. Целевая функция отражает качество найденного решения и представляет собой длину маршрута. Важнейшей частью ГА является скрещивание (кроссовер) отдельных индивидов для создания потомков [8]. В рассмотренных задачах в скрещивании участвует каждая хромосома, но в задаче коммивояжера пара ей выбирается случайным образом из всей популяции, а в задаче поиска кратчайшего пути в графе случайным образом из условно-определенной популяции. По значениям целевой функции лучшая часть родителей и лучшая часть потомков в определенной пропорциональности переходят в следующее поколение. Количество поколений определяет количество итераций в цикле, увеличивая это значение можно найти более точное решение [2].
В первую очередь рассмотрим задачу коммивояжера, иначе TSP (TravellingSalesmanProblem), в которой требуется найти кратчайший замкнутый маршрут, проходящий через все его вершины один раз с возвратом в исходную вершину [9].
Для этой задачи было проанализировано несколько вариантов скрещивания и отбора особей в следующее поколение [3, 4], но наиболее эффективным по опытным данным оказался нижеприведенный метод.
Например, в задаче необходимо найти путь среди ![]() городов. Генерируется популяция из
городов. Генерируется популяция из ![]() хромосом, первая по счету из которых, к примеру, имеет код
хромосом, первая по счету из которых, к примеру, имеет код![]() . Заметим, что в данном алгоритме хромосома представляет собой последовательность прохождения точек
. Заметим, что в данном алгоритме хромосома представляет собой последовательность прохождения точек![]() , где
, где ![]() . Далее случайным образом производится отбор пары для данной хромосомы из всей популяции. Допустим, была выбрана восьмая по счету хромосома с кодом
. Далее случайным образом производится отбор пары для данной хромосомы из всей популяции. Допустим, была выбрана восьмая по счету хромосома с кодом ![]() . Затем происходит оперирование с
. Затем происходит оперирование с ![]() , выбирается случайным образом интервал длиной
, выбирается случайным образом интервал длиной ![]() и вырезается из
и вырезается из ![]() этот отрезок в какой-либо части. Пусть была выбрана последовательность 23456, она присваивается потомку в ту же позицию
этот отрезок в какой-либо части. Пусть была выбрана последовательность 23456, она присваивается потомку в ту же позицию ![]() , что и в
, что и в ![]() . Теперь для заполнения пустых ячеек (*) делается перебор от конца хромосомы-родителя
. Теперь для заполнения пустых ячеек (*) делается перебор от конца хромосомы-родителя ![]() . Взято число 3, проверяется – имеется ли оно в
. Взято число 3, проверяется – имеется ли оно в ![]() . Оно уже находится в ячейке
. Оно уже находится в ячейке ![]() между значениями 2 и 4. Взято число 7, его еще нет, поэтому оно записывается в первую пустую ячейку. В результате имеется
между значениями 2 и 4. Взято число 7, его еще нет, поэтому оно записывается в первую пустую ячейку. В результате имеется ![]() . На следующем шаге получается
. На следующем шаге получается ![]() , а на последнем
, а на последнем![]() . Из двух родительских хромосом выходит одна дочерняя, в отличие от классического генетического алгоритма, где в потомках – две хромосомы. Далее вышеприведенный алгоритм скрещивания применяется также и для девяти оставшихся индивидов
. Из двух родительских хромосом выходит одна дочерняя, в отличие от классического генетического алгоритма, где в потомках – две хромосомы. Далее вышеприведенный алгоритм скрещивания применяется также и для девяти оставшихся индивидов ![]() . В результате в скрещивании участвует каждая хромосома, и пара ей выбирается случайным образом. На выходе имеется дочерняя популяция, по размеру равная родительской, но в следующее поколение переходят 60 % лучших, по значениям целевой функции, родительских хромосом и 40 % – дочерних. Данное соотношение подобрано экспериментальным путем. Было замечено, что увеличение доли дочерних индивидов в последующей популяции приводит к ухудшению будущих потомков, а уменьшение их доли – к замедлению темпов эволюции. Однако данное скрещивание имеет недостаток – темпы развития сильно замедляются с увеличением количества точек, что делает данный способ кроссовера неэффективным при очень большом количестве городов, но этот недостаток устраняют разработанные нижеописанные модификации.
. В результате в скрещивании участвует каждая хромосома, и пара ей выбирается случайным образом. На выходе имеется дочерняя популяция, по размеру равная родительской, но в следующее поколение переходят 60 % лучших, по значениям целевой функции, родительских хромосом и 40 % – дочерних. Данное соотношение подобрано экспериментальным путем. Было замечено, что увеличение доли дочерних индивидов в последующей популяции приводит к ухудшению будущих потомков, а уменьшение их доли – к замедлению темпов эволюции. Однако данное скрещивание имеет недостаток – темпы развития сильно замедляются с увеличением количества точек, что делает данный способ кроссовера неэффективным при очень большом количестве городов, но этот недостаток устраняют разработанные нижеописанные модификации.
Оператор мутации используется после операций скрещивания [4]. Он применяется ко всей полученной популяции в целом: после сортировки родительских и дочерних хромосом по значениям целевой функции выбирается половина худших индивидов. С некоторой заданной величиной вероятности каждый индивид в худшей половине подвергается мутации – перестановке двух произвольных чисел (генов). Например, если имелось на входе 012345, то на выходе может выйти 312045, где числа 0 и 3 поменялись местами. Данный оператор позволяет частично улучшить значения целевой функции у неудачных индивидов, оставляя неизменными эффективные решения. По экспериментальным данным было получено, что оптимальной вероятностью использования оператора мутации является 3–8 %.
Для исследования и сравнительного анализа разработанного генетического алгоритма средствами MicrosoftVisualStudio на языке C# был реализован программный комплекс [5–7]. На его основе проводилось исследование, настройка и оптимизация параметров ГА, таких как: инициализация начальной популяции, оператор скрещивания, оператор мутации, отбор в следующее поколение и других. Также были разработаны некоторые модификации для генетического алгоритма, что позволило повысить его эффективность в несколько раз. На рисунке 1 можно увидеть пример работы ГА для 60 точек.
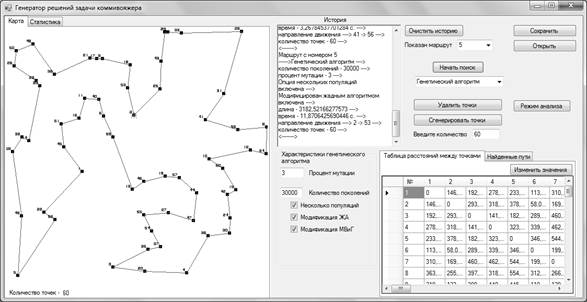
Рисунок 1. Пример работы генетического алгоритма
Из рисунка видно, что при выборе генетического алгоритма можно использовать в качестве опций некоторые его модификации – «модификация жадным алгоритмом», «несколько популяций» и «модификация методом ветвей и границ». В первом варианте начальная популяция генерируется не случайным образом, а с предварительным применением жадного алгоритма («идти в ближайший») к каждой точке (городу). Такая модификация ускоряет процесс сходимости к оптимуму, но также увеличивается вероятность нахождения не самого оптимального решения («тупик») при большом количестве точек. Эту проблему немного устраняет вторая модификация ГА, которая дает указание на развитие не одной популяции, а сразу нескольким не зависящим друг от друга популяциям. Однако в конце лучшие хромосомы из каждой популяции будут объединены в одну, работа с которой будет проводиться обычным образом. Заметим, что в этом случае объединяются несколько вариантов «тупика», что приводит к улучшению общего результата. Не менее важное значение несет в себе третья модификация, которая увеличивает каждую популяцию в два раза (то есть ведется обработка популяции из 2*N хромосом), дополняя ее результатами работы метода ветвей и границ в количестве 0,5*N и случайными последовательностями также 0,5*N.
Для исследования полученных результатов и проведения сравнительного анализа эффективности работы методов был разработан отдельный модуль [5].
На рисунке 2 видны длины найденных маршрутов для 50–110 точек, найденных различными алгоритмами: ГА с тремя различными модификациями для 10000 поколений, ГА без модификаций для 10000 поколений, а также жадным алгоритмом и методом наименьших отрезков.
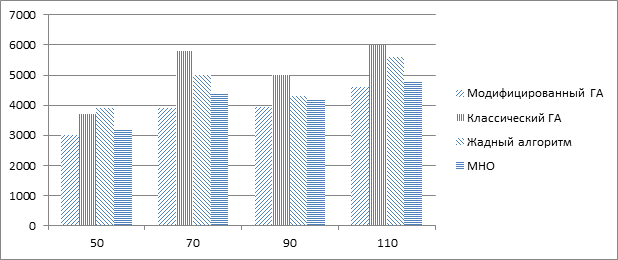
Рисунок 2. Гистограмма длин найденных маршрутов различными алгоритмами при количестве городов от 50 до 110
Следует заметить, что генетический алгоритм с тремя модификациями для 10000 поколений всегда находит более эффективное решение, чем другие методы оптимизации; однако возрастают временные затраты на поиск. Алгоритм позволяет варьировать параметры длины найденного маршрута и длительности его работы, то есть при увеличении количества поколений улучшается точность найденного пути относительно оптимального, но времени затрачивается больше. Данный вывод был сделан во время проведения исследований эффективности работы алгоритма для 350 городов, где уже 10000 поколений недостаточно, и увеличение количества поколений в четыре раза повышает, хоть и незначительно, точность найденного решения.
Также следует отметить, что зависимость затрачиваемого на поиск решения времени от количества городов имеет ярко выраженную экспоненциальную форму, что видно из рисунка 3. На рисунке отражены результаты работы ГА только с модификацией жадным алгоритмом.
Рассмотрим далее задачу поиска кратчайшего пути в графе. Специфика данной задачи в том, что граф накладывает существенные ограничения на реализацию генетического алгоритма, так как заранее определены начальная и конечная точки (они задаются пользователем). Кроме того граф не обязательно должен являться полным, т.е. возможности реализации скрещивания в генетическом алгоритме в значительной степени ограничены отношениями инцидентности в графе.
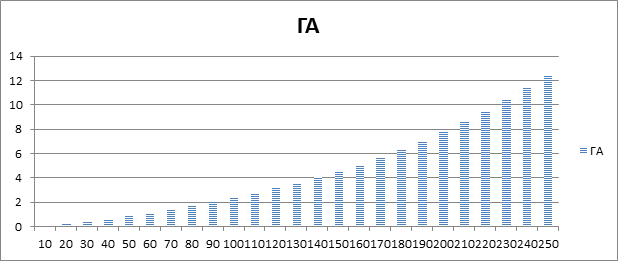
Рисунок 3. Зависимость времени поиска маршрутов генетическим алгоритмом при количестве городов от 10 до 250
Поэтому была осуществлена настройка параметров ГА с учетом особенностей задачи поиска пути в графе. В частности, из-за ограничений, накладываемых графом, алгоритм скрещивания хромосом для данной задачи существенно отличается от классического [2]: для скрещивания необходимо, чтобы родительские особи обладали одинаковыми узлами (первый и последний не рассматриваются, т.к. они схожи у всех особей). Если родительские особи обладают несколькими одинаковыми узлами, то случайным образом выбирается узел разрыва, и производится скрещивание: из двух родительских особей получаются два потомка.
Например, пусть даны две хромосомы разной длины – 1,4,6,45,38,9 и 1,6,7,19,45,67,22,9. Для двух родителей производится поиск одинаковых узлов (начальная и конечная точки не учитываются). В указанном примере скрещивание можно произвести путем обмена участками, начинающимися – с 6, либо с 45. Случайным образом выбирается точка разрыва (6 или 45), и хромосомы обмениваются участками. Допустим, была выбрана точка 45, получим: для первой хромосомы 1,4,6,*,*,* и *,*,*,45,38,17; для второй хромосомы – 1,6,7,19,*,*,*,* и *,*,*,*,45,67,22,17. На следующем шаге располагаем двумя потомками: 1,4,6,45,67,22,17 и 1,6,7,19,45,38,17.
В кроссовере участвует каждая хромосома; в разработанном авторами генетическом алгоритме используются три разновидности скрещивания: «лучшие с лучшими» – скрещивание хромосом с наименьшимзначением длины пути между собой; «лучшие с худшими» – скрещивание хромосом с наименьшимзначением длины пути и хромосом с заведомо неэффективным решением (позволяет внести генетическое разнообразие и найти новые варианты пути), случайное скрещивание – производится скрещивание случайно выбранных хромосом, безотносительно значения длины пути.
Исследования эффективности работы генетического алгоритма применительно к задаче нахождения кратчайшего пути в графе показали, что данный метод при небольшом количестве точек (около 100) практически всегда находит наилучший результат. Однако из-за существенных ограничений, накладываемых графом, использование генетического алгоритма в рассматриваемой задаче далеконе всегда дает оптимальные результаты. Классические методы нахождения кратчайшего пути в графе (такие, например, как метод индексации) оказались более эффективными: метод индексации осуществляет поиск в 1000 раз быстрее генетического алгоритма и всегда находит кратчайший путь.
Выводы
В заключение необходимо отметить ряд закономерностей, выявленных в результате исследований:
- Генетические алгоритмы доказали свою эффективность как в задачах с малым числом ограничений, так и в задачках с большим числом ограничений. ГА всегда находят эффективное решение, которое зачастую является оптимальным.
- В задачах с малым числом ограничений, ГА показали большую эффективность, нежели классические методы. При относительно небольших временных затратах, ГА находят лучший путь.
- Существенным преимуществом ГА является то, что они позволяют варьировать параметры поиска, т.е. например, если имеется 2 параметра: длина пути и время поиска, возможно, увеличивая затраты одного параметра (времени), получать выигрыш в другом параметре (сокращение длины найденного пути).
- В комбинаторных задачах с большим числом ограничений, несмотря на то, что ГА находят эффективное решение, следует отдать предпочтение классическому методу индексации, т.к. в данных условиях он работает значительно быстрее и всегда находит оптимальный результат.
Рецензенты:
Видовский Леонид Адольфович, д.т.н., доцент, профессор кафедры ИСП ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.
Ключко Владимир Игнатьевич, д.т.н., профессор кафедры ИСП ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.



