В эксплуатации газотурбинных двигателей случаются поломки конической шестерни коробки приводов, приводящие к выключению авиационного двигателя в полёте [1]. По результатам исследования одного из таких случаев было установлено, что поломки носят усталостный характер. Тензометрирование показало, что максимальные вибронапряжения возникают по форме колебаний с тремя узловыми диаметрами. Отстройка от резонанса, путём изменения геометрии, не представляется возможным для зубчатых колёс подобного типа. В качестве решения проблемы было предложено повышение демпфирующей способности элемента.
Одним из способов повышения демпфирующей способности в конических шестернях является использование конструкционного демпфирования. Конструкционное демпфирование связано с особенностями конструкции и подразумевает под собой обширный класс различных конструкционных решений, от динамических гасителей колебаний до сухого трения в сочленениях [4], [5]. В данной работе рассмотрены демпферы тарельчатого типа и предложен метод проектирования демпфера с учетом динамического поведения конической шестерни.
Для анализа работы демпфера при колебаниях конической шестерни и оценки эффективности демпфирования был проведён ряд расчётов в конечно-элементном пакете ANSYS.
1. На первом этапе проводились статические расчёты в двухмерной (2D) постановке для оценки жёсткости демпфера и анализа контактного взаимодействия шестерни и демпфера. Определялись необходимые величины натяга посадки демпфера. Также на данном этапе проводился анализ технологических особенностей конструкции шестерни: например, установлено, что допуск на положение некоторых контактных площадок составляет до 40, что делает крайне сложным обеспечить полное прилегание контактных поверхностей.
На рисунке 1 показаны различные варианты расположения контактной зоны тарельчатого демпфера к шестерне.
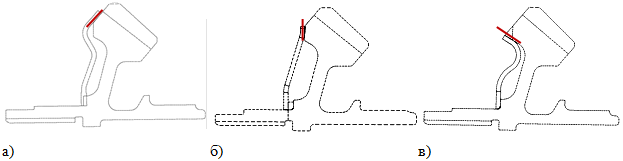
Рис. 1. Варианты расположения тарельчатого демпфера: а) демпфер с контактом по верхней поверхности, б) демпфер с контактом по вертикальной поверхности, в) демпфер с контактом по нижней поверхности
Данные конструкции демпферов можно разделить на три группы по варианту сопряжения с шестерней по поверхности контакта (поверхности трения): по верхней поверхности (рис. 1а); по вертикальной поверхности (рис. 1б); по нижней поверхности (рис. 1в) (для реализации представленного на рисунке случая необходимо изменение геометрии шестерни).
По результатам расчета в двумерной постановке проведена оценка нормального усилия на поверхностях контакта демпфера и шестерни. Получена зависимость нормального усилия на поверхности трения от величины натяга для различных конструкций демпферов (рис. 2). Зависимость подчиняется линейно-возрастающему закону.
Согласно результатам расчетов тарельчатые демпферы были разделены по жёсткости на три группы (рис. 2):
– мягкие демпферы – данные конструкции представляют собой изогнутую тарелку;
– демпферы средней жесткости – данная конструкция имеет вид тарелки в виде конуса;
– демпфер максимальной жёсткости – это самый короткий в радиальном направлении демпфер из рассматриваемых, имеющий поверхность трения по нижней грани шестерни.
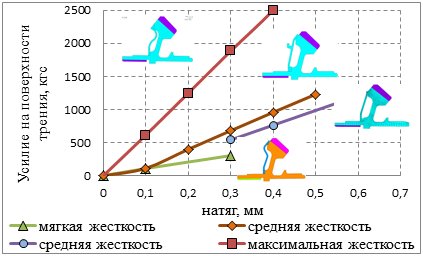
Рис. 2. Нормальное усилие на контактной поверхности для различных вариантов демпферов на рабочем режиме с оборотами шестерни
Также выявлено, что центробежные силы незначительно влияют на нормальное усилие, а именно – уменьшают давление в контакте на ~ 5–10 %.
На поверхностях трения, в процессе колебаний, шестерни будет реализовываться проскальзывание демпфера относительно шестерни, и за счёт работы сил трения будет происходить демпфирование колебаний. Работа силы трения между поверхностями зависит от величины проскальзывания и нормального усилия и вычисляется по формуле:
, (1)
где 
– работа силы трения;
– коэффициент сухого трения;
– нормальное усилие;
– величина проскальзывания.
Как видно из уравнения (1), чем выше нормальное усилие, тем выше сила трения.
На последующих этапах были исследованы два демпфера: демпфер исходной конструкции (рис. 1а) и демпфер новой конструкции (рис. 1б), спроектированный с учетом конструктивных особенностей шестерни.
2. На втором этапе проводились расчёты собственных форм и частот колебаний демпфера и конической шестерни в трёхмерной (3D) постановке. Предполагалось, что совпадение собственной частоты демпфера с частотой шестерни ведёт к увеличению проскальзывания в контактирующих зонах, что положительно будет влиять на демпфирование колебаний шестерни.
По результатам тензометрирования шестерни было выявлено, что максимальные динамические напряжения имеют место по форме с тремя узловыми окружностями с частотой f1. Таким образом, геометрия нового демпфера подбиралась такая, чтобы одна из форм колебаний совпадала или была близка к собственной частоте шестерни f1 по форме с тремя узловыми окружностями.
Анализ результатов расчёта собственных форм и частот тарельчатых демпферов показал, что:
– демпфер исходной конструкции имеет две собственные формы, близкие по частоте с f1. Это формы с одной узловой окружностью и ноль узловых диаметров, и с ноль узловых окружностей, и шесть узловых диаметров;
– демпфер новой конструкции был спроектирован так, что имеет одну собственную частоту, совпадающую сf1. Это форма с ноль узловых окружностей и семь узловых диаметров.
3. На третьем этапе проводились расчёты, учитывающие нестационарные процессы по времени при вынужденных колебаниях в 3D постановке.
Расчёт переходных динамических процессов (Transient Analysis) является методом, используемым для определения динамического поведения системы при действии любых зависящих от времени нагрузок.
В данном расчёте анализировалось поведение демпфера, и проводился анализ контактного взаимодействия поверхностей трения между шестернёй и демпфером. Для этого была разработана следующая методика: проводился расчет вынужденных колебаний при известном законе движения одного тела – шестерни, и рассчитывался отклик демпфера на воздействие со стороны колеблющейся шестерни.
В такой постановке анализировалось поведение демпфера, и проводился анализ контактного взаимодействия поверхностей трения между шестерней и демпфером. Данный подход был выбран по следующим причинам:
– для решения задачи нет необходимости построения всей модели шестерни с демпфером целиком, т.е. в расчётной модели присутствуют только части шестерни, имеющие поверхности соприкосновения с демпфером, а демпфер присутствует целиком. Данное упрощение модели позволяет существенно сократить размерность задачи и в относительно короткое время провести расчёт;
– расчёты для оценки демпфирующей способности демпфера можно проводить по конкретным интересующим нас формам колебаний шестерни и соответствующей амплитуде напряжений или перемещений.
К основному минусу данной методики можно отнести следующее:
– при взаимодействии с демпфером собственная частота и собственная форма шестерни может измениться, что при данной постановке не может быть учтено, поскольку закон движения шестерни задан по результатам расчёта её колебаний. Поэтому предполагалось, что шестерня является массивным телом, и демпфер не будет значительно влиять на собственную форму колебаний шестерни.
В расчётной модели задавались следующие граничные условия (рис. 3):
– гармонический закон колебания шестерни брался из расчета собственных форм и частот колебаний полноразмерной модели шестерни. Закон прикладывался в виде перемещений на узлы. Уровень перемещений шестерни соответствовал уровню напряжений, зарегистрированному при тензометрировании шестерни;
– гармонический закон проецировался на отдельные части объёма шестерни: на выделенный объём большого венца шестерни и на выделенный объём вала шестерни;
– между тарельчатым демпфером и выделенными объёмами задавался контакт: по контактирующей поверхности со стороны большого модуля задавался стандартный контакт; по контактирующей поверхности вала шестерни задавался контакт без возможности отрыва и проскальзывания, так как в этой части происходил зажим гайкой.
Контактное взаимодействие на поверхности конической шестерни рождает нелинейность задачи, которая обусловлена наличием сухого трения (Кулоновского трения), вследствие чего контакт может иметь различный статус: прилипание, скольжение, зазор (нет контакта).
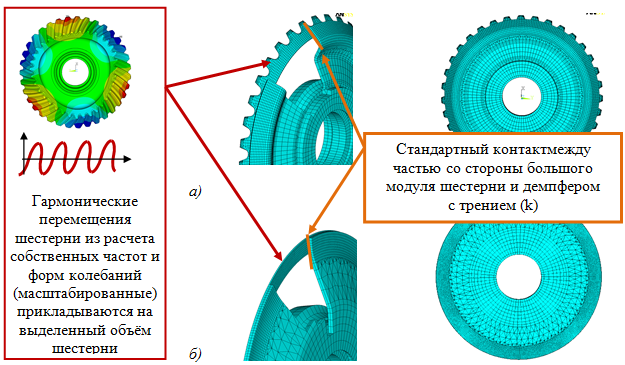
Рис. 3. Конечно-элементная модель и граничные условия расчетной модели: а) демпфер исходной конструкции в составе шестерни, б) демпфер доработанной конструкции в составе шестерни
По результатам расчёта определялся отклик демпфера при вынужденных колебаниях шестерни, и высчитывалась совершённая работа силы трения на контактной поверхности между демпфером и шестернёй (рис. 4). На рисунке 4 показан отклик демпфера на колебания шестерни и совершённая работа силы трения по времени.
Затраченную работу силы трения переводили в логарифмический декремент колебаний через кинетическую энергию шестерни по формуле [6]:
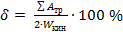, (2)
где 
– логарифмический декремент колебаний (%); 
– суммарная работа силы трения, совершённая за один период колебания; 
– кинетическая энергия демпфируемового тела.
Следуя методикам, были получены следующие зависимости:
– зависимость логарифмического декремента колебаний от величины натяга и коэффициента трения (линейно-возрастающий закон);
– зависимость роста логарифмического декремента колебаний при совпадении собственной частоты колебаний шестерни и демпфера (значительное возрастание затраченной работы силы трения).
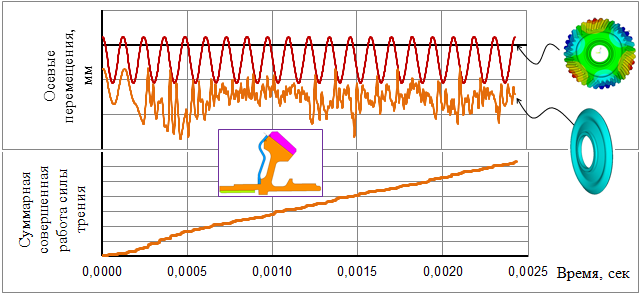
Рис. 4. Сверху – графики осевых перемещений шестерни и тарельчатого демпфера (исходная конструкция). Снизу – график суммарной совершённой работы силы трения
На рисунке 5 показано, что демпфер, спроектированный с учётом динамического поведения конструкции (совпадение собственной частоты), совершает значительно больше работы силы трения, чем первоначальный вариант демпфера.
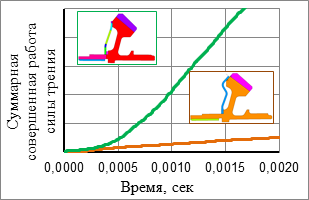
Рис. 5.График суммарной совершённой работы силы трения по времени для демпфера исходной конструкции и демпфера, спроектированного с учётом динамического поведения конструкции
В предположении, что демпфер будет снижать уровень динамических напряжений, был проведён анализ изменения коэффициента демпфирования при более низких уровнях возбуждения. Для анализа были проведены расчёты с возбуждением, соответствующим меньшим вибронапряжениям в шестерне. Результаты расчета показали, что логарифмический декремент колебаний изменяется незначительно и поддерживается на высоком уровне.
Основные преимущества данной конструкции тарельчатого демпфера объясняются следующими особенностями:
– совпадение собственной частоты шестерни с собственной частотой демпфера;
– собственная форма колебаний тарелки имеет семь узловых диаметров, что не кратно собственной форме шестерни, имеющей три узловых диаметра. Возможно, что это приводит к большим значениям проскальзывания между поверхностями трения.
Для проверки эффективности данного демпфера для конической шестерни коробки приводов запланированы экспериментальные исследования.
Рецензенты:
Августинович В. Г., д-р техн. наук, заместитель начальника ОКБ по науке, ОАО «Авиадвигатель», г. Пермь.
Нихамкин М. Ш., д-р техн. наук, профессор, зам. заведующего кафедрой «Авиационные двигатели», ПНИПУ, г. Пермь.