Введение
При проектировании и оптимизации многих электрофизических устройств, работающих в переменном электромагнитном поле (ЭМП), возникает необходимость расчета их параметров с учетом проникновения (диффузии) ЭМП в массивные ферромагнитные проводники. Такими проводниками могут быть электромагнитные экраны, роторы электромашинных генераторов и нагреваемые детали в устройствах индукционного нагрева. В настоящее время при расчете диффузии ЭМП широкое применение получили численные методы прямого решения уравнений электродинамики. Однако такое решение приводит к чрезмерно большим затратам машинного времени и во многих случаях затрудняет анализ влияния ЭМП на такие параметры проводников, как сопротивление, индуктивность, глубина проникновения ЭМП в проводник и температура. Исследования существенно упрощаются с использованием параметров поверхностного слоя (скин-слоя) проводников [1–5]. Поэтому расчет параметров скин-слоя массивных ферромагнитных проводников с учетом их нагрева и нелинейных магнитных свойств представляется актуальной задачей.
Цель данной работы заключается в получении формул для инженерного расчета параметров скин-слоя массивных ферромагнитных проводников в установившемся режиме при синусоидальном ЭМП.
Допущения
Для получения расчетных формул сделаем следующие допущения.
1. Известную кривую намагничивания Bc(Hc) как нелинейную зависимость магнитной индукции Bc от магнитной напряженности Hc ферромагнитного (стального) проводника приближенно заменим совокупностью прямолинейных отрезков (рис. 1), каждый из которых на интервале изменения напряженности 
и индукции 
(
) запишется так:
, (1)
при постоянной дифференциальной магнитной проницаемости
(2)
и изменяющейся статической магнитной проницаемости
. (3)
2. Поверхностный слой проводника представим в виде совокупности n-слоев, причем в каждом (k+1)-слое, согласно рис. 1, амплитуда магнитной напряженности Hc изменяется от Hck до Hck+1 при постоянной дифференциальной магнитной проницаемости μdk+1. При этом координате zk соответствует амплитуда напряженности Hck, а координате zk+1 – амплитуда напряженности Hck+1, причем координаты zk и zk+1 отсчитываются от поверхности проводника.
3. Каждый (k+1)-слой проводника имеет постоянную удельную проводимость [5]
(4)
при постоянной усредненной температуре этого слоя 
и постоянных температурных коэффициентах 
, причем 
– удельная проводимость при температуре 
, которая была у проводника до воздействия ЭМП.
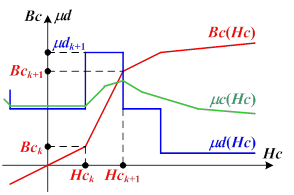
Рис. 1. Характерные графики зависимостей магнитной индукции Bc(Hc), статической μc(Hc) и дифференциальной μd(Hc) магнитных проницаемостей ферромагнитного проводника от магнитной напряженности Hc
4. Нагрев каждого (k+1)-слоя проводника происходит адиабатно (без учета теплоотдачи в окружающую среду) при постоянной удельной теплоемкости СT и постоянной объемной плотности 
проводника [5].
5. Для всего поверхностного слоя проводника введем постоянные эквивалентные параметры: толщина скин-слоя 
, статическая магнитная проницаемость 
, удельная проводимость 
и температура 
.
6. Размеры массивных проводников и радиусы кривизны их поверхности существенно превосходят глубину проникновения в них ЭМП, поэтому будем исходить из представления о плоской одномерной электромагнитной волне, проникающей в проводящее полупространство перпендикулярно его поверхности и полностью затухающей в его теле [2; 4].
Методика расчета
Совместим границу проводящего полупространства с плоскостью x0y в декартовой системе координат (рис. 2), так что для плоской одномерной электромагнитной волны векторы напряженностей электрического 
и магнитного 
полей имеют по одной составляющей [1; 4]:
; 
;
причем это касается и вектора магнитной индукции
,
где 
– единичные векторы, направленные по осям x и y соответственно.
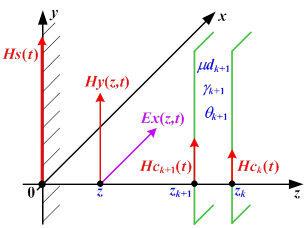
Рис. 2. Расчетная модель проводящего полупространства
В этом случае процесс проникновения ЭМП в (k+1)-слой проводника описывается следующим уравнением [1; 2; 4]
(5)
при плотности тока
. (6)
Примем, что при 
электромагнитная волна полностью затухает, тогда граничные условия имеют вид (рис. 2):
(7)
причем для синусоидально изменяющегося во времени электромагнитного поля имеем синусоидальные магнитные напряженности:
. (8)
На основании уравнений (5–8) согласно [2] для (k+1)-слоя находим магнитную напряженность:
(9)
и плотность тока:
, (10)
где:
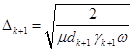. (11)
Из соотношений (7–9) для магнитной напряженности 
получаем координату, начальную фазу и толщину (k+1)-слоя соответственно:
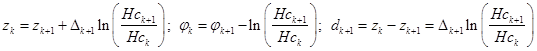, (12)
причем для поверхностного n-слоя при 
имеем:
; (13)
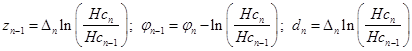. (14)
Далее на основании (3, 9) для (k+1)-слоя находим магнитную индукцию:
. (15)
С учетом (10, 11) определим среднюю мощность тепловых потерь в (k+1)-слое проводника [2; 4]:
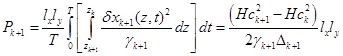, (16)
где lx и ly – размеры проводника по осям x и y соответственно (рис. 2);
– период.
При адиабатном нагреве (k+1)-слоя можно записать уравнение [5]:
, (17)
тогда с учетом (11, 12, 16, 17) при длительности воздействия ЭМП 
получаем усредненную температуру этого слоя:
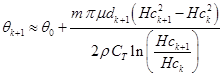, (18)
где 
– число периодов Т напряженностей (8).
Таким образом, зная температуру (18), по формуле (4) можно рассчитать удельную проводимость (k+1)-слоя и мощность тепловых потерь (16).
Затем определим для (k+1)-слоя усредненные максимальные значения магнитного потока:
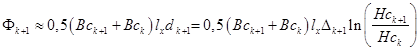(19)
и магнитной энергии:
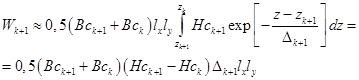. (20)
Для расчета эквивалентных параметров всего скин-слоя проводника 
с учетом (16, 17) найдем суммарную мощность тепловых потерь в скин-слое толщиной :
(21)
и на основании (12, 18) определим температуру этого слоя:
. (22)
Из (21) и (22) при находим эквивалентную толщину скин-слоя:
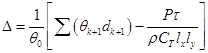. (23)
После расчета (23) и (22) определяем по (4) удельную проводимость скин-слоя :
. (24)
Далее с учетом (19, 20) для скин-слоя толщиной найдем усредненное максимальное значение магнитной индукции:
, (25)
а из уравнения для максимальной магнитной энергии
(26)
получим формулу для расчета эквивалентной статической магнитной проницаемости:
. (27)
Если по проводнику вдоль оси x (рис. 2) проходит синусоидальный ток с амплитудой 
при максимальной магнитной напряженности на его поверхности 
, тогда из уравнений для мощности (21) и магнитной энергии (26)
(28)
найдем сопротивление R и внутреннюю индуктивность L проводника:
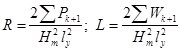. (29)
Результаты расчета
По формулам (1–29) проведены расчеты параметров массивного проводника из малоуглеродистой стали [1; 5]: 
(Гн/м); 
(°С); 
(См/м); 
(1/°С); 
(1/°С2); 
(кг/м3); 
(Дж/кг·°С); 
(м); 
(1/с); 
(мс); 
; 
(с). Исходные и рассчитанные параметры массивного проводника из малоуглеродистой стали приведены в табл. 1.
Таблица 1
Параметры массивного проводника из малоуглеродистой стали при частоте f=5000 (Гц)
|
k+1 |
– |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Bck+1 |
Тл |
0,1 |
0,5 |
1 |
1,3 |
1,5 |
2 |
2,3 |
|
Hck+1 |
А/м |
100 |
200 |
500 |
1000 |
2000 |
10000 |
20000 |
|
|
– |
796 |
3183 |
1326 |
477 |
159 |
50 |
24 |
|
|
°С |
20,04 |
23,49 |
27,69 |
33,07 |
37,43 |
95,08 |
281,48 |
|
|
МСм/м |
7 |
6,87 |
6,71 |
6,52 |
6,37 |
4,78 |
2,29 |
|
|
мм |
0,095 |
0,048 |
0,075 |
0,128 |
0,224 |
0,461 |
0,962 |
|
|
мм |
|
0,033 |
0,069 |
0,088 |
0,155 |
0,743 |
0,667 |
|
zk+1 |
мм |
1,755 |
1,722 |
1,653 |
1,565 |
1,410 |
0,667 |
0 |
|
Pk+1 |
Вт |
7,491 |
45,371 |
207,364 |
450,825 |
1053 |
21750 |
68010 |
|
|
мВб |
0,022 |
0,01 |
0,052 |
0,102 |
0,217 |
1,300 |
1,434 |
|
Wk+1 |
мДж |
0,477 |
1,444 |
17 |
73 |
313 |
6461 |
20686 |
|
P |
Wm |
Bm |
|
|
|
|
R |
L |
|
Вт |
Дж |
Тл |
– |
МСм/м |
°С |
мм |
мкОм |
мкГн |
|
91520 |
27,552 |
1,429 |
65 |
4,14 |
126,92 |
2,195 |
457,6 |
0,138 |
На рис. 3 для 
и различных моментов времени приведены расчетные графики зависимостей напряженности (а) и индукции (б) от глубины проникновения z ЭМП.
Заключение
1. Предложена методика определения параметров скин-слоя массивных ферромагнитных проводников с учетом их нагрева и нелинейных магнитных свойств, которая может использоваться для инженерного расчета ферромагнитных электромагнитных экранов, роторов электромашинных генераторов и нагреваемых деталей в устройствах индукционного нагрева.
а)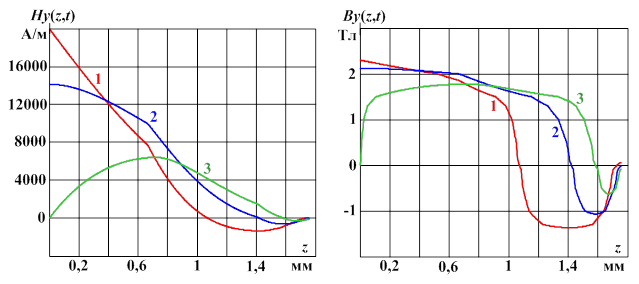
б)
Рис. 3. Расчетные графики зависимостей напряженности (а) и индукции (б) от глубины проникновения z ЭМП в ферромагнитный проводник: 1 – 
; 2 – 
; 3 – 
2. Температура поверхностного слоя при адиабатном нагреве не зависит от удельной проводимости проводника и определяется дифференциальной магнитной проницаемостью, удельной теплоемкостью и объемной плотностью проводника, а также максимальными значениями магнитной напряженности и числом периодов её изменения.
3. Для поверхностного слоя с увеличением максимальной магнитной напряженности возрастают мощность тепловых потерь, магнитный поток, магнитная энергия и температура.
Рецензенты:
Усов Юрий Петрович, д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Канев Федор Юрьевич, д.ф.-м.н., ведущий научный сотрудник Института оптики атмосферы им. В.Е. Зуева СО РАН, г. Томск.