1. Введение. В современной экономике широко используются экономические и финансовые индикаторы, отражающие состояние сложной системы в данный момент времени и служащие для понимания процессов, происходящих в ней, для корректировки управления, а также дающих возможность для анализа и изменения поведения исследуемой системы в целом. В связи с таким широким использованием индикаторов системы важной является проблема обеспечения высокого качества результатов экономического анализа. Среди подобных исследований особо выделим проблему соотношения показателей, полученных моделированием какого-нибудь типа, к их фактическим величинам. Случайные ошибки, возникающие при измерении характеристик экономических явлений, в сочетании со случайными ошибками модели могут оказывать существенное влияние на конечный результат исследований. Поэтому актуальной является задача определения границ множеств, соответствующих допустимым значениям факторов системы, а, значит, дающих приемлемую в рамках данной задачи вероятность ошибки (риск) и не допускающих ошибочных выводов о состоянии системы.
Проблема появления неправильных решений при измерении различных индикаторов экономических систем систематически начала изучаться в работах [1-3]. Дело в том, что ошибки измерения могут принципиально исказить представление о состоянии экономической системы в целом и, следовательно, повлиять на правильность принимаемого решения. Оказывается, что ошибки модели играют аналогичную роль, и более того, совместное появление названных ошибок может существенно усилить этот отрицательный эффект. Именно изучение влияния ошибок моделирования на оценку состояния сложной системы и представляет цель настоящей работы. Отметим, что некоторые частные случаи данной задачи изучены в [4]: определение границ допустимого множества параметров производилось через область изменения независимого фактора. В данной статье рассмотрен наиболее общий подход к определению допустимых множеств. Наконец, в работе указаны способы управления риском: наряду с уже известными [4], предложен новый метод снижения последствий ошибок, который базируется на корректировке параметров эконометрической модели.
2. Постановка задачи и вычисление рисков. Пусть на выходе системы или ее отдельных подсистем имеет место некоторый процесс ![]() , зависящий от фактора
, зависящий от фактора ![]() , то есть
, то есть ![]() . Рассмотрим случай, когда зависимость между процессом
. Рассмотрим случай, когда зависимость между процессом ![]() и фактором
и фактором ![]() устанавливается с помощью линейной регрессии, т.е. имеет форму
устанавливается с помощью линейной регрессии, т.е. имеет форму ![]() , где
, где ![]() коэффициенты модели, а
коэффициенты модели, а ![]() ошибка модели, обладающая «классическими» свойствами, ошибка и факторы независимы. Будем предполагать, что значения переменной
ошибка модели, обладающая «классическими» свойствами, ошибка и факторы независимы. Будем предполагать, что значения переменной ![]() измерены с ошибкой:
измерены с ошибкой:
![]() ,
,
где волна означает измеренное значение переменной.
Тогда рассматриваемая модель может быть представлена в следующем виде:
![]() . (1)
. (1)
Видно, что при использовании модели вида (1) совокупная ошибка складывается не только из случайной ошибки построения модели, но и из ошибки измерения переменной ![]() .
.
Особо определим оценочную величину ![]() :
:
![]() . (2)
. (2)
Предположим, что состояния рассматриваемой системы можно разбить на два класса: 1) множество состояний, когда система не способна выполнять свои целевые назначения; 2) множество состояний, при которых функционирование системы обеспечивает выполнение каких-либо целевых установок. Первое множество состояний назовем (ср. с [2]) множеством опасных состояний, а второе - множеством допустимых фактических состояний и обозначим его через ![]() . Рассмотрим случай, когда
. Рассмотрим случай, когда ![]() . Заметим, что при измерении
. Заметим, что при измерении ![]() возникает ошибка
возникает ошибка ![]() , и, следовательно, в общем случае
, и, следовательно, в общем случае ![]() . Это неравенство может привести к ситуации, в которой фактическое значение
. Это неравенство может привести к ситуации, в которой фактическое значение ![]() , а измеренное значение
, а измеренное значение ![]() , то есть система находится в области опасного состояния, а измеренные величины об этом не сигнализируют. Таким образом, необходимо учитывать ошибку измерения
, то есть система находится в области опасного состояния, а измеренные величины об этом не сигнализируют. Таким образом, необходимо учитывать ошибку измерения ![]() , а значит необходимо вводить новую область
, а значит необходимо вводить новую область ![]() , лежащую внутри
, лежащую внутри ![]() и позволяющую создать некоторый запас надежности. Методы построения подобных областей можно найти, например, в [2; 5].
и позволяющую создать некоторый запас надежности. Методы построения подобных областей можно найти, например, в [2; 5].
В случае, когда для нахождения ![]() используется модель вида (1), возникают дополнительные сложности с решением вопроса о нахождении
используется модель вида (1), возникают дополнительные сложности с решением вопроса о нахождении ![]() в
в ![]() , так как
, так как ![]() заменяется своими оценочными значениями из (2). Следуя [2], рассмотрим ситуации, соответствующие различным положениям в пространстве переменных системы относительно описанных множеств. Введем событие
заменяется своими оценочными значениями из (2). Следуя [2], рассмотрим ситуации, соответствующие различным положениям в пространстве переменных системы относительно описанных множеств. Введем событие ![]() , означающее что
, означающее что ![]() . Будем говорить, что произошло событие
. Будем говорить, что произошло событие ![]() , если
, если ![]() . Через
. Через ![]() обозначим события, противоположные событиям
обозначим события, противоположные событиям ![]() соответственно.
соответственно.
Рассмотрим теперь возможные комбинации этих событий.
![]() – состояние системы, когда фактическое состояние системы допустимо, с помощью средств оценки поступает информация также о допустимом состоянии;
– состояние системы, когда фактическое состояние системы допустимо, с помощью средств оценки поступает информация также о допустимом состоянии;
![]() – фактическое состояние находится вне области допустимых границ, оценочная информация подтверждает это состояние;
– фактическое состояние находится вне области допустимых границ, оценочная информация подтверждает это состояние;
![]() – по оценочной информации фиксируется недопустимое состояние системы, хотя фактическое значение находится в допустимой области;
– по оценочной информации фиксируется недопустимое состояние системы, хотя фактическое значение находится в допустимой области;
![]() – оценочная модель дает информацию о допустимом состоянии системы, фактическое значение находится вне допустимой области.
– оценочная модель дает информацию о допустимом состоянии системы, фактическое значение находится вне допустимой области.
В первых двух случаях анализ состояния системы показывает корректность построенной эконометрической зависимости. Последние два события характеризуются потерями ввиду неправильной оценки состояния системы. Область ![]() назовем (ср. с [2]) областью ложной оценки, так как она характеризуется появлением ложной информации о выходе системы в область опасных состояний, хотя система находится в допустимых режимах. Область
назовем (ср. с [2]) областью ложной оценки, так как она характеризуется появлением ложной информации о выходе системы в область опасных состояний, хотя система находится в допустимых режимах. Область ![]() назовем областью опасной ситуации, так как в этом случае модель, по сути, допускает использование данных, на которые она не рассчитана, что приводит к крайне недостоверным результатам.
назовем областью опасной ситуации, так как в этом случае модель, по сути, допускает использование данных, на которые она не рассчитана, что приводит к крайне недостоверным результатам.
Таким образом, при использовании модели (1) часть данных будет располагаться относительно допустимых областей таким образом, что вероятным станет наступление событий ![]() и
и ![]() , которые приведут к ошибкам. Это означает, что совокупный риск использования модели можно оценить как вероятность
, которые приведут к ошибкам. Это означает, что совокупный риск использования модели можно оценить как вероятность ![]() нахождения данных в области ложной оценки и области опасной ситуации.
нахождения данных в области ложной оценки и области опасной ситуации.
Для численного определения таких вероятностей можно использовать подход, изложенный в [2].
Очевидно
![]() . (3)
. (3)
С учетом (1), (2) имеем
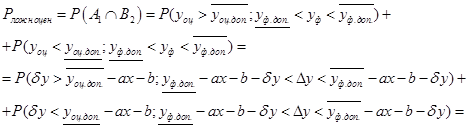
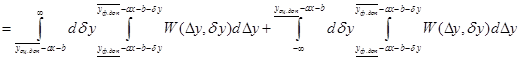 .
.
Аналогично
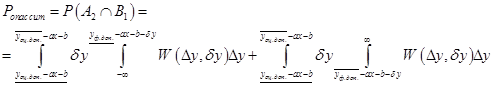 .
.
Здесь – совместная плотность распределения отклонений. Вид подынтегральной функции и основные факторы, подлежащие учету при ее формировании, определяются объектами или подсистемами процесса и их режимом работы, а также множеством других факторов.
Рассмотрим теперь вопрос управления рисками. Ранее, в работе [4], были предложены следующие способы: 1) увеличением объема исходных данных или сужением области изменения независимой переменной добиться снижения риска; 2) снижением качества эконометрической модели обеспечить необходимый уровень риска. При дальнейшем рассмотрении оказалось, что оба этих метода имеют существенные недостатки. Так, действия в первом направлении на практике фактически могут состоять только в сужении области измерений, что ограничивает поле применения модели, при этом все же недостаточно снижая показатели риска. Действия во втором направлении позволяли получить приемлемые показатели вероятности ошибочных действий только при существенном снижении качества регрессии, что почти нивелировало полученное преимущество.
Имея в виду вышесказанное, предложим еще один способ управления риском, состоящий в перерасчете коэффициентов эконометрической модели с целью обеспечения нахождения данных исключительно в области ![]() , что должно исключить высокую вероятность ошибки, возникающую при выходе полученных при помощи регрессионной зависимости значений из области
, что должно исключить высокую вероятность ошибки, возникающую при выходе полученных при помощи регрессионной зависимости значений из области ![]() , и оставить только риск, связанный с ошибками
, и оставить только риск, связанный с ошибками ![]() и
и ![]() .
.
На практике действия в этом направлении будут означать использование специальных коэффициентов регрессии, найденных путем решения задачи квадратичного программирования:
![]()
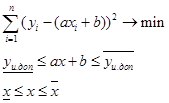 (4)
(4)
где ![]() и
и ![]() - минимальное и максимальное значение переменной
- минимальное и максимальное значение переменной ![]() из выборки. Несмотря на то что предлагаемый способ также может привести к потере качества модели, на практике часто оказывается, что такой подход наиболее рационален. В следующем пункте данной статьи обсудим введенные понятия на конкретном примере.
из выборки. Несмотря на то что предлагаемый способ также может привести к потере качества модели, на практике часто оказывается, что такой подход наиболее рационален. В следующем пункте данной статьи обсудим введенные понятия на конкретном примере.
3. Определение стоимости квартиры. Воспользуемся примером, рассмотренным в работе [4]. Построим линейную регрессионную модель, описывающую зависимость стоимости квартиры от ее площади. Полученная в [4] модель имеет вид:
![]() , (5)
, (5)
где![]() – стоимость квартиры (млн руб.),
– стоимость квартиры (млн руб.), ![]() – общая площадь (кв. м) квартиры,
– общая площадь (кв. м) квартиры, ![]() – ошибка модели. Оценки параметров эконометрической модели здесь являются эффективными, точность построенной модели характеризуется коэффициентом детерминации (
– ошибка модели. Оценки параметров эконометрической модели здесь являются эффективными, точность построенной модели характеризуется коэффициентом детерминации (![]() ), равным 0,83. Таким образом, качество построенной модели (5) является достаточно высоким.
), равным 0,83. Таким образом, качество построенной модели (5) является достаточно высоким.
Специфика полученной модели состоит в возможности ошибки при оценке квартиры, ввиду влияния на цену отличных от площади, менее значимых факторов (наличие балкона, ремонт, планировка и т.п.). Исследуемую модель (5) будем считать эконометрической моделью с ошибкой в зависимой переменной [3]. Исходные данные отличаются от фактических значений на отклонение ![]() (
(![]() ).
).
Оценка рынка недвижимости показывает, что допустимыми фактическими границами являются ![]() . Определим теперь границы оценочного допустимого множества исходя из его назначения: создания некоторого запаса надежности. Определим используемую модель как модель, надежность которой оценивается по критерию возврата брака, т.е. по отказам потребителя принимать к рассмотрению квартиры, оцененные с помощью модели. В этом случае, согласно принятому ГОСТу [5], допустимым является установление коэффициента запаса экспертными методами. Для данного класса недвижимости в агентствах недвижимости принято давать запас надежности в 5% для нижней границы стоимости и в 30% для верхней границы стоимости (имеется в виду, что близость к предельным ценам «отпугивает» покупателей, и поэтому нижние цены завышаются либо квартиры переводят в другой ранг, а квартиры с верхними ценами занижают или переводят в другой ранг). Таким образом, определим
. Определим теперь границы оценочного допустимого множества исходя из его назначения: создания некоторого запаса надежности. Определим используемую модель как модель, надежность которой оценивается по критерию возврата брака, т.е. по отказам потребителя принимать к рассмотрению квартиры, оцененные с помощью модели. В этом случае, согласно принятому ГОСТу [5], допустимым является установление коэффициента запаса экспертными методами. Для данного класса недвижимости в агентствах недвижимости принято давать запас надежности в 5% для нижней границы стоимости и в 30% для верхней границы стоимости (имеется в виду, что близость к предельным ценам «отпугивает» покупателей, и поэтому нижние цены завышаются либо квартиры переводят в другой ранг, а квартиры с верхними ценами занижают или переводят в другой ранг). Таким образом, определим ![]() .
.
Отклонение ![]() считаем имеющим нормальное распределение с
считаем имеющим нормальное распределение с ![]() и
и ![]() . С помощью критерия согласия Пирсона была проверена гипотеза о нормальности распределения ошибки модели
. С помощью критерия согласия Пирсона была проверена гипотеза о нормальности распределения ошибки модели ![]() . Таким образом, плотность
. Таким образом, плотность ![]() из (3) соответствует двумерному нормальному распределению, и, следовательно, вероятность из (3) может быть найдена. На рисунке 1 представлена зависимость риска от конкретной величины независимой переменной (площади квартиры).
из (3) соответствует двумерному нормальному распределению, и, следовательно, вероятность из (3) может быть найдена. На рисунке 1 представлена зависимость риска от конкретной величины независимой переменной (площади квартиры).
![]()
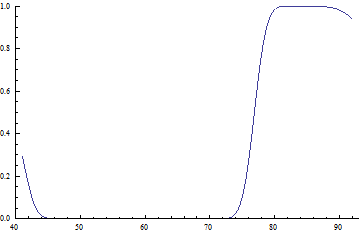
х, площадь квартиры (кв. м)
Рисунок 1
Как можно видеть из графика, риск довольно высок на краях рассматриваемой области изменения площади квартиры ![]() . Особенно выделяется промежуток (86,95), на котором риск крайне высок – равен 1. Это связано с тем, что полученные при помощи модели значения
. Особенно выделяется промежуток (86,95), на котором риск крайне высок – равен 1. Это связано с тем, что полученные при помощи модели значения ![]() на этом интервале выходят за границы допустимой области
на этом интервале выходят за границы допустимой области ![]() .
.
Применим для данной задачи описанный выше способ управления риском: построим новую регрессионную зависимость, используя специальные коэффициенты.
Решив задачу квадратичного программирования
![]()
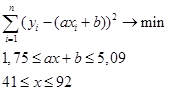 ,
,
получим коэффициенты ![]() ,
, ![]() , коэффициент детерминации
, коэффициент детерминации ![]() при этом равен 0,67. На рисунке 2 хорошо видно, что новая линия регрессии (отмеченная зеленым) целиком принадлежит области
при этом равен 0,67. На рисунке 2 хорошо видно, что новая линия регрессии (отмеченная зеленым) целиком принадлежит области ![]() (границы которой отмечены синим пунктиром), в отличие от первоначальной линии регрессии (отмеченной желтым), которая выходит из допустимой оценочной области на множестве значений
(границы которой отмечены синим пунктиром), в отличие от первоначальной линии регрессии (отмеченной желтым), которая выходит из допустимой оценочной области на множестве значений ![]() (86;95).
(86;95).
![]()
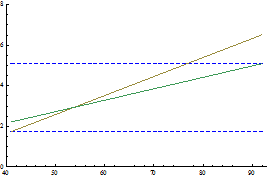
х, площадь квартиры (кв. м)
Рисунок 2
На рисунке 3 представлена кривая, описывающая риск, возникающий при использовании модели с коэффициентами, полученными специальным образом.
![]()
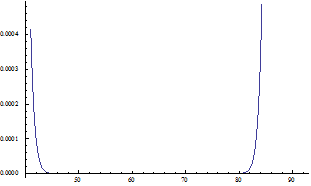
х, площадь квартиры (кв. м)
Рисунок 3
Видно, риск упал практически до 0 на всей области изменения ![]() . Такой хороший результат получен потому, что в рамках данной модели удалось изменить регрессию таким образом, что даже суммарное максимальное значение всех ошибок, возникающих при использовании данной модели, не выводит переменную
. Такой хороший результат получен потому, что в рамках данной модели удалось изменить регрессию таким образом, что даже суммарное максимальное значение всех ошибок, возникающих при использовании данной модели, не выводит переменную ![]() из допустимой оценочной области. Кроме того, коэффициент детерминации для специальных параметров регрессии остается достаточно высоким, что позволяет считать новую модель высококачественной. Однако в общем случае эти условия могут не выполняться, и тогда следует ожидать значительного, но не полного падения риска. Отметим, что в [4] рассмотрена задача определения регрессии с
из допустимой оценочной области. Кроме того, коэффициент детерминации для специальных параметров регрессии остается достаточно высоким, что позволяет считать новую модель высококачественной. Однако в общем случае эти условия могут не выполняться, и тогда следует ожидать значительного, но не полного падения риска. Отметим, что в [4] рассмотрена задача определения регрессии с ![]() , результатом решения которой стала регрессия с
, результатом решения которой стала регрессия с ![]() , т.е. предлагаемый здесь метод оказывается более рациональным по сравнению с методом из [4].
, т.е. предлагаемый здесь метод оказывается более рациональным по сравнению с методом из [4].
Выводы. В данной работе представлен случай, когда экономические индикаторы моделируются при помощи линейной однофакторной регрессии. Показано, что в случае использования такой модели может возникать вероятность принятия ошибочного решения (риск). Риск возникает в связи с неправильной информацией о нахождении параметров системы в допустимой области или вне ее. Предложен способ интерпретации и определения границ области, возникающей при введении запаса надежности. Получены формулы для определения вероятности принятия ошибочного решения в таких системах. Описан метод управления риском, который оказывается более действенным во многих ситуациях по сравнению с методами из [4]. Результаты статьи проиллюстрированы на примере влияния площади квартиры на ее рыночную стоимость. Предложенный метод управления риском в данном примере дает абсолютное падение вероятности ошибочного решения.
Рецензенты:
Елохова Ирина Владимировна, д.э.н., профессор, заведующий кафедрой «Управление финансами» Пермского национального исследовательского университета, г. Пермь.
Долгова Елена Владимировна, д.э.н., профессор кафедры «Информационные технологии и автоматизированные системы» Пермского национального исследовательского университета, г. Пермь.



