Важнейшим параметром тонкой сегнетоэлектрической пленки является ее критический размер. Если толщина пленки соизмерима с критическим размером, то диэлектрический отклик такой пленки зависит от ее толщины, и в этом случае говорят о размерном эффекте в пленке. Проявляется размерный эффект как в изменении значения диэлектрической проницаемости, так и в смещении точки фазового перехода по сравнению с объемным материалом.
Как показывают экспериментальные и теоретические исследования тонких пленок кислородсодержащих сегнетоэлектриков типа BaxSr1-xTiO3 (BST), температура фазового перехода Тс таких пленок может смещаться как в область более высоких значений, так и в обратную сторону при изменении толщины пленки [1-7]. Такая неоднозначность в поведении температуры фазового перехода обусловлена вкладом в размерный эффект разных физических явлений. К появлению размерного эффекта в тонкой пленке сегнетоэлектрика типа смещения могут привести три основных фактора: 1) пространственная дисперсия сегнетоэлектрической моды и вид граничных условий для поляризации на поверхностях пленки; 2) влияние механических напряжений, вызванных рассогласованием постоянных решетки пленки и подложки (несобственный размерный эффект); 3) различие коэффициентов линейного расширения пленки и подложки. Все три фактора могут присутствовать одновременно, но вносить различный вклад в размерный эффект.
Экспериментальным подтверждением дисперсии мягкой сегнетоэлектрической моды в тонких пленках являются опыты по неупругому рассеянию нейтронов, в результате которых получают дисперсионные кривые для поперечных оптических колебаний [4-6]. Пространственное распределение поляризации P в сегнетоэлектрическом слое является решением уравнения, полученного из разложения термодинамического потенциала по параметру порядка фазового перехода (в данном случае по поляризации), описанного Гинзбургом и Девонширом. Пространственная дисперсия в уравнении Гинзбурга-Девоншира в одномерной постановке задачи (вдоль оси х, направленной ортогонально к поверхности пленки) описывается квадратом градиента поляризации, который преобразуется во вторую производную по координате.
Возникающая под действием внешнего поля динамическая поляризация в тонкой пленке, так же как и спонтанная поляризация, испытывает влияние размерного эффекта. Для одномерного случая в параэлектрическом состоянии (Т > Tc) пространственное распределение поляризации находят из решения уравнения Гинзбурга-Девоншира:
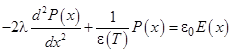. (1)
В сегнетоэлектрическом состоянии (Т < Tc) уравнение Гинзбурга-Девоншира для спонтанной поляризации имеет вид:
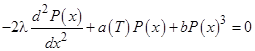, (2)
где: 
, b - коэффициенты разложения Ландау; l – корреляционный параметр материала.
В среде, близкой к линейному состоянию, пренебрегая нелинейным членом и введя в выражение (2) радиус корреляции 
:
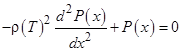, (2¢)
где ε(Т) – диэлектрическая проницаемость объемного материала при однородной поляризации, определяемая в соответствии с законом Кюри-Вейса.
Радиус корреляции r является функцией температуры и имеет максимальное значение в области фазового перехода (рис. 1). В случае нелокальной связи сегнетоэлектрическая поляризация не может быть изменена на расстоянии меньшем, чем корреляционный радиус, что и приводит к возникновению размерного эффекта. Введем критический размер сегнетоэлектрической пленки. Как правило, под критическим размером в сегнетоэлектрике понимается минимальный размер образца, при котором исчезают его сегнетоэлектрические свойства, и он становится обычным линейным диэлектриком. Мы предлагаем рассматривать в качестве критического размер образца, при котором начинает проявляться размерный эффект, т.е. когда материал еще проявляет сегнетоэлектрические свойства, но все его характеристики начинают зависеть от его размеров. Критическим размером, с этой позиции, является удвоенное значение корреляционного радиуса: hкр(T) = 2ρ(T). Для BaTiO3 (Tc = 395 K) при комнатной температуре и λ=10-8 мкм2 значение критического размера составляет hкр(T) @ 8 нм, в то время как при 400 К, т.е. вблизи фазового перехода hкр(T) @ 50 нм, что сопоставимо с толщинами пленок, активно используемых в настоящее время в микроэлектронике.
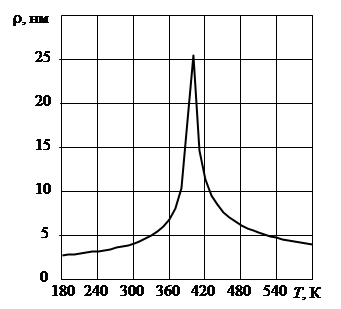
Рис. 1. Температурная зависимость радиуса корреляции пленки BaTiO3 (l1 = 24.24×10-8 мкм2).
Вид распределения и динамической (парафаза), и спонтанной (сегнетофаза) поляризации в слое сегнетоэлектрика определяется граничными условиями на его поверхности. Размерному эффекту отвечают граничные условия вида:
, (3)
В работе [8] на основе анализа полученных авторами результатов исследования кислородсодержащих сегнетоэлектрических кристаллов, в частности исследовались мелкие кристаллы BaTiO3, с помощью дифракции рентгеновского излучения (метод Дебая-Шеррера), делается заключение о существовании на поверхности кристалла тетрагональной деформации решетки. Тетрагональная спонтанная деформация (растяжение) решетки, измеренная с помощью метода Дебая-Шеррера, не исчезает даже при температурах, превышающих температуру Кюри макроскопического кристалла на сотни градусов Цельсия.
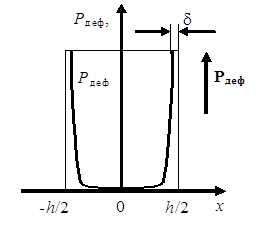
Рис. 2. Распределение в сегнетоэлектрической пленке поляризации, связанной с механической деформацией
Расчет электростатического потенциала точечной решетки на поверхности и в объеме ионного кристалла путем применения собственных функций прямоугольного объема [9] показал, что в поверхностном слое кристалла возникает сильное электрическое поле, которое практически полностью спадает на расстоянии порядка d = 3-4 постоянных решетки. Это поле вызывает касательную поляризацию ионов в поверхностном слое (рис. 2). Таким образом, и в параэлектрическом, и в сегнетоэлектрическом состоянии в поверхностном слое сегнетоэлектрика, имеющего структуру перовскита, толщиной порядка нескольких постоянных решетки, существует поляризация, вызванная механической деформацией решетки. Блокировка сегнетоэлектрической поляризации на поверхностях пленки происходит за счет возникновения касательной поляризации в сегнетоэлектрическом слое толщины d, а не за счет растяжения пленки из-за рассогласования постоянных решеток пленки и подложки.
Если направление приложенного поля и динамической поляризации ортогонально поверхности слоя, то результирующее распределение поляризации будет стремиться к нулю на границе слоя, что соответствует наличию размерного эффекта. Вследствие пространственной дисперсии величина поляризации будет плавно спадать от максимального значения в глубине сегнетоэлектрической пленки до нуля на ее поверхности. В случае полного соответствия решеток сегнетоэлектрика и материала, с которым он граничит, а также их ориентации, поляризация в сегнетоэлектрике постоянна и размерного эффекта в данном случае не наблюдается при любой толщине пленки.
Рассмотрим размерный эффект в параэлектрическом состоянии. Для случая divD = 0: D = P(x) + e0E(x) и граничных условий (3) решение уравнения (1) имеет вид [1]:
, 
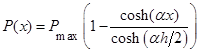(4)
Тогда эффективная диэлектрическая проницаемость тонкой плёнки [10]:
. (5)
Для простоты описания распределения сегнетоэлектрической поляризации в плоскопараллельных тонкопленочных сегнетоэлектрических конденсаторах используют так называемую модель мертвого слоя [10]:
.
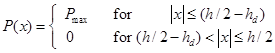Мертвый слой – слой линейного диэлектрика толщиной 
с проницаемостью 
, расположенный между электродом и сегнетоэлектрической пленкой. Эффективная диэлектрическая проницаемость пленки в модели мертвого слоя:
. (6)
Параметры мертвого слоя были экспериментально определены из исследований вольтфарадных и вольтамперных характеристик тонкопленочных конденсаторов на основе Ba0.7Sr0.3TiO3 [11]: 
, 
.
Сопоставив выражение (6) с эффективной диэлектрической проницаемостью сегнетоэлектрической пленки, найденной с учетом корреляционных явлений (5), получим выражение для толщины мертвого слоя: 
. Для пленки Ba0.5Sr0.5TiO3 и @ 40, l @ 1.25´10-10 нм: @ 40, 
@ 2 нм.
В работе [7] приводится обзор оценок размера, при котором сегнетоэлектрик теряет свои нелинейные свойства. По данным, полученным разными авторами, его значения составляют порядка 2-3 нм.
Толщина мертвого слоя, а, следовательно, и размер образца, при котором он теряет свои сегнетоэлектрические свойства, определяется пространственной дисперсией сегнетоэлектрической моды. При этом полученные разными путями значения размера образца, при котором он теряет свои сегнетоэлектрические свойства, практически совпадают и могут рассматриваться как достаточно надежные.
Исходя из вышеизложенного, логично толщину мертвого слоя рассматривать в качестве минимальной толщины сегнетоэлектрической пленки, при которой материал пленки перестает быть сегнетоэлектриком.
Рассмотрим решение уравнения (2) для тонкой сегнетоэлектрической пленки в составе плоскопараллельного конденсатора с нулевыми граничными условиями (3), находящейся в сегнетофазе. В силу того что уравнение (2) с такими граничными условиями можно решить только численными методами, представим его решение в виде ряда. Зависимость поляризации от координаты в этом случае [12]:
, (7)
где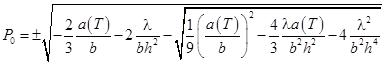 
.
В общем случае l является тензором четвертого ранга, но в среде с кубической кристаллической структурой в корреляционном тензоре ненулевыми являются только три компоненты: l1; l2; l3 [1; 2].
На рис. 3 приведены температурные зависимости поляризации при различной ориентации вектора поляризации относительно плоскости пленки BaTiO3 для двух толщин пленки h = 50 и 300 нм, рассчитанные по (7).
а)
б)
Рис. 3. Зависимость спонтанной поляризации от температуры для пленок BaTiO3 различной толщины: (а) – вектор поляризации параллелен поверхности пленки; (б) – вектор поляризации ортогонален поверхности пленки.
Ориентация вектора поляризации учитывалась с использованием соответствующих компонент корреляционного тензора: при ориентации вектора поляризации параллельно поверхности пленки - l3 = 10-8 мкм2; при ориентации вектора поляризации ортогонально поверхности пленки - l1 = 24.24×10-8 мкм2. Соответственно и радиус корреляции будет различен при различной ориентации вектора поляризации, что, по-видимому, связано с тем, что жесткость подрешеток сегнетоэлектрика по отношению к сжатию или растяжению гораздо больше, чем по отношению к сдвиговой деформации.
На рис. 3б кривые для трех толщин пленок совпали, что говорит о том, что в пленках таких толщин при параллельной ориентации вектора поляризации относительно плоскости пленки размерный эффект не появляется.
Температура Кюри в условиях размерного эффекта:
, (8)
где для BaTiO3: температура фазового перехода в объемном материале TC = 395 K; постоянная Кюри-Вейса С = 1.6×105 К.
Зависимость температуры Кюри от толщины пленки в соответствии с (8) приведена на рис. 4. Из сравнения кривых на рис. 4а и 4б, так же как и на рис. 3, наглядно видно, что если вектор поляризации ориентирован параллельно плоскости пленки, то размерный эффект возникает при толщинах пленки менее 40 нм, а если ортогонально, то – при толщинах менее 100 нм. Сделанные численные оценки критической толщины пленки позволяют исследователю заранее предсказать и учесть наличие размерного эффекта в образцах.
(а) 
(б)
Рис. 4. Зависимость температуры Кюри от толщины пленки: (а) – вектор поляризации параллелен поверхности пленки; (б) – вектор поляризации ортогонален поверхности пленки.
Таким образом, размерный эффект проявляется в зависимости диэлектрической проницаемости и температуры фазового перехода от толщины пленки. Одной из основных причин появления размерного эффекта является пространственная дисперсия сегнетоэлектрической моды и вид граничных условий для сегнетоэлектрической поляризации на поверхности пленки. Наиболее важной характеристикой размерного эффекта является корреляционный параметр λ, значение которого определяет как корреляционный радиус, а соответственно критический размер пленки, при котором возникает размерный эффект, так и критический размер пленки, при котором она теряет сегнетоэлектрические свойства.
Работа выполнена при поддержке Министерства образования и науки ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» госконтракта № 11.519.11.1001 и проекта FP7-IRSES MultiWaveS № 247532.
Рецензенты:
Головков Александр Алексеевич, д.т.н., профессор, профессор кафедры радиоэлектронных средств ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)» Минобрнауки России, г. Санкт-Петербург.
Баранов Игорь Владимирович, д.т.н., профессор, заведующий кафедрой «Физика ИХиБТ», заместитель директора института холода и биотехнологий ФГБОУ ВПО «Санкт-Петербургский национальный исследовательский университет информационных технологий механики и оптики» Минобрнауки России, г. Санкт-Петербург.