Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Электротехнические комплексы электроснабжения потребителей первой категории особой группы используются в центрах хранения данных, многофункциональных высотных зданиях, нефтяной и газодобывающей промышленности, геологоразведке, других отраслях промышленности и народного хозяйства. Отличительной особенностью таких систем является наличие дополнительного питания от третьего независимого взаимно резервирующего источника питания, в качестве которого применяют источник бесперебойного электропитания на основе аккумуляторных батарей и дизельные генераторы, объединённые в дизельную электростанцию

Опубликованы работы [1-4], в которых рассмотрены вопросы управления дизель-генераторными установками (ДГУ) в переходных режимах работы. Однако одной из основных задач проектирования комплексов электроснабжения потребителей первой категории особой группы является выбор количества и мощности дизель-генераторных установок (ДГУ) в составе дизельной электростанции (ДЭС), от правильного решения которой зависит эффективность электротехнического комплекса на этапах его реализации и эксплуатации.

Ранее авторами были получены уравнения и неравенства параметрической модели дизельной электростанции. Модель дизельной электростанции основана на предложенном понятии коэффициентов минимальной и максимальной загрузки дизельной электростанции

, , (1)

где – номинальная мощность ДЭС на n-й ступени,, – номинальная мощность ДГУ i-й ступени.

Коэффициент минимальной загрузки ступени ДЭС равен минимальному отношению мощности, потребляемой нагрузкой, к текущей номинальной мощности электростанции, при котором исключается холостой ход дизельных двигателей, включенных в работу. Коэффициент максимальной загрузки ступени ДЭС определяет отношение мощности, потребляемой нагрузкой, к текущей номинальной мощности электростанции, при котором осуществляется переключение на следующую по мощности ступень.

Параметрическая модель дизельной электростанции представлена в виде системы неравенств, которая описывает ограничения мощности отдельных ДГУ, в соответствии с условиями на загрузку ДЭС:

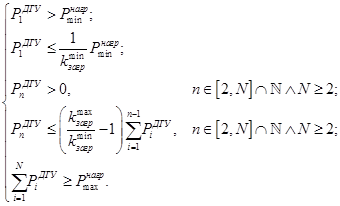(2)

Введено понятие образа стандартной номинальной мощности на множестве стоимостей

(3)

где – упорядоченный набор значений стоимости ДГУ; – отображение множества стандартной мощности на множество ; – стоимость ДГУ с номинальной стандартной мощностью .

Целью исследования является разработка методов поиска оптимальных параметров дизельной электростанции, описываемой системой (2) и условием (3).

Материал и методы исследования

Возможны следующие формальные постановки задачи оптимизации параметров дизельной электростанции.

Задача I: найти

, , (4)

где – общее число ступеней ДЭС, .

Задача II: найти

, , (5)

где - стандартная мощность ступени ДГУ.

Задача III: найти вектор параметров дизель-генераторных установок, обеспечивающих минимальную стоимость электростанции

,. (6)

Задача IV: найти вектор параметров дизель-генераторных установок, обеспечивающих минимальную стоимость электростанции и топлива, потребляемого за период эксплуатации

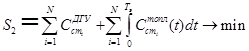. (7)

Задача I характеризуется непрерывной функцией мощности ДГУ, задача II – дискретной.

Для решения задачи I выразим максимально допустимую номинальную мощность ступени ДЭС в функции номера ступени:

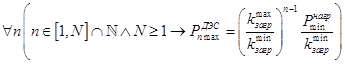. (8)

Общая номинальная мощность ДЭС должна обеспечивать ее работу во всем диапазоне нагрузки. Верхнее ее значение определяется объединением выражения с неравенством из системы (2):

. (9)

Тогда число ступеней ДЭС определяется неравенством, следующим из выражений (8), (9):

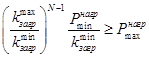, (10)

где – максимальная мощность нагрузки, при которой необходимо обеспечить длительную работу ДЭС.

Выражение (10) дает оценку нижней границы числа ступеней ДЭС и, следовательно, числа ДГУ при заданном диапазоне мощности нагрузки:

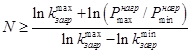. (11)

Неравенство позволяет оценить минимальное число ДГУ в составе ДЭС, необходимое для обеспечения ее работы в заданном диапазоне мощностей с заданной загрузкой дизельных двигателей.

Для решения задачи в постановке II разработаны алгоритм и программа. Алгоритм решения включает следующие шаги: 1) мощности отдельных ДГУ выбираются последовательно и в соответствии с системой неравенств (2); 2) расчетная мощность ДГУ округляется до ближайшего меньшего значения из ряда стандартных значений номинальной мощности; 3) после каждого шага делается проверка ДЭС на способность обеспечить энергией максимальную нагрузку, что соответствует последнему выражению системы (2); 4) на последнем этапе мощность ДГУ последней ступени корректируется: она соответствует наименьшей стандартной мощности, превышающей разность между мощностью максимальной длительной нагрузки и номинальной мощностью предпоследней ступени ДЭС. Алгоритм позволяет произвести более точную оценку минимального количества ДГУ для обеспечения работы ДЭС в заданном диапазоне мощностей с заданной загрузкой дизельных двигателей с учетом дискретности функции мощности.

Решение задачи минимизации стоимости в постановке III основано на том, что имеется отображение (3) множества номинальной стандартной мощности ДГУ на множество стоимостей.

Тогда пространство возможных решений

можно представить матрицей, где строка представляет возможное решение, а номер столбца соответствует номеру ступени ДЭС.

В пространстве S выделим область допустимых решений, удовлетворяющих системе неравенств (2). Для этого выделим в пространстве , представляющем собой n-ю декартову степень множества действительных чисел, область , которую можно интерпретировать как множество удовлетворяющих системе (2) векторов , компоненты которых являются действительными числами.

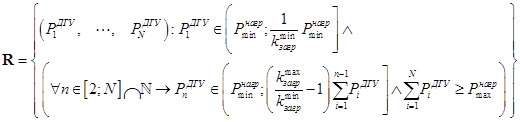. (12)

Множество допустимых решений определяется пересечением этих множеств:

(13)

Для решения задачи оптимизации нужно выбрать вектор из множества такой, чтобы стоимость элементов этого вектора была наименьшей. Или формально:

.

Геометрическая интерпретация множества R как области в N-мерном гильбертовом пространстве, ограниченной гиперплоскостями согласно системе неравенств (2), для случая трех ступеней ДЭС, представлена на рис. 1.

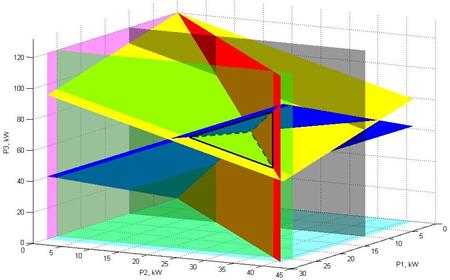
Рисунок 1 – Трехмерная область R

черный – P1min, пурпурный - P2min, голубой – P3min, зеленый – Р1max, красный – Р2max,

синий – Р3max, желтый (Р1+Р2+Р3)min

Из анализа рис. 2 следует, что имеются дополнительные ограничения на диапазон возможных значений номинальной мощности для любой ступени ДЭС при известном количестве ступеней.

Ограничение на нижнее значение ДГУ n-й ступени в функции номинальных мощностей предыдущих ступеней:

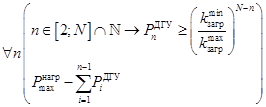. (14)

Тогда с учетом системы неравенств (2) и выражения (14) можно записать диапазон возможных значений номинальной мощности для любой ступени ДЭС при известном количестве ступеней:

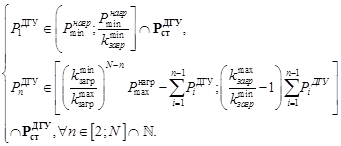(15)

Последнее выражение уточняет и дополняет систему неравенств (2).

Разработаны алгоритм и программа решения задачи оптимизации параметров дизельной электростанции в постановке III.

Алгоритм решения задачи оптимизации основан на использовании функции кодирования, переводящей множество допустимых решений во множество кодировок [5], и содержит следующие шаги.

– из множеств допустимой мощности и стоимости ДГУ формируют матрицы, соответствующие области возможных решений S и области отображения таким образом, что соответствующие друг другу элементы этих матриц имеют одинаковые индексы;

– из областей S и удаляются решения, которые не удовлетворяют системе (2), и получают матрицы, соответствующие областям Dи где– множество допустимых кодировок;

– в матрице, изображающей область , отыскиваются строки с минимальной суммой элементов, причем строки являются образами одноименных строк из матрицы, которой представлена область D, которые и являются решением задачи оптимизации.

Результаты исследования и их обсуждение

Произведен выбор оптимальных параметров ДГУ в составе ДЭС для следующих исходных данных: производитель ДГУ – Wilson, ряд мощностей ДГУ – [11; 14,4; 17,6; 26,4; 40; 44; 52; 704; 88; 120; 132; 160; 20; 220; 280; 320; 400] кВт, функции стоимости ДГУ Wilson для различных исполнений (по данным открытых источников) представлены на рис. 2.

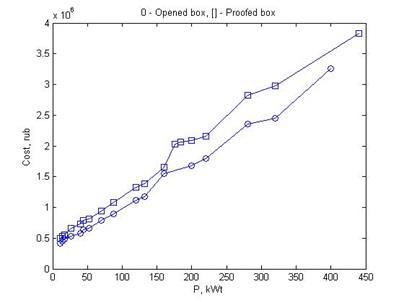
Рисунок 2 – Функции стоимости ДГУ Wilson для различных исполнений

Результаты решения задачи оптимизации, которыми являются множества значений мощности ДГУ в составе ДЭС, приведены в табл. 1. Важной является последовательность компонентов множества мощностей, так как она определяет последовательность включения ДГУ в работу.

Таблица 1 – Результаты решения задачи оптимизации

Из анализа полученных результатов следует, что существенное влияние на количество ДГУ в составе ДЭС и распределение их мощности оказывает соотношение минимальной и максимальной мощности ДЭС при длительной работе и , а также вид функциональной зависимости стоимости ДГУ от мощности. Увеличение стоимости в случае использования нескольких ДГУ меньшей мощности оправдывается значительным улучшением условий функционирования ДГУ при малых нагрузках дизельной электростанции и уменьшением эксплуатационных затрат на приобретение топлива.

Выводы

Таким образом, поставлена и решена задача оптимального проектирования дизельной электростанции для питания потребителей первой категории особой группы с учетом ограничения на коэффициент загрузки дизель-генераторных установок. Результаты решения представлены в форме ряда мощностей дизель-генераторных установок в составе дизельной электростанции, последовательность элементов в котором определяет последовательность включения дизель-генераторных установок в работу.

Рецензенты:

Носырев Михаил Борисович, д.т.н., профессор, первый проректор, Уральский государственный горный университет, г. Екатеринбург.

Зобнин Борис Борисович, д.т.н., профессор, Уральский государственный горный университет, г. Екатеринбург.