Повышение упругости строительной фанеры (СФ) способствует повышению ее надежности и долговечности, а также позволяет наиболее полно использовать все возможности конструкционного материала. Деформационные превращения, происходящие при изменении нагрузки, температуры, и влажности СФ, лежат в основе многих технологических процессов ее обработки: прессования, сушки, а также при эксплуатации конструкций [3, 5]. Распространённый дефект при сушке и лущении шпона характеризуется чередующимися выпуклостями и впадинами, высота и протяженность которых неодинакова по ширине и длине листа. Одна из возможностей устранения дефекта шероховатости – это обработка листов шпона жидким эластомером (рис. 1). В связи с этой модификацией листов шпона перед склеиванием фанеры изменяется физико-механическое состояние субстрата.

Рисунок 1- Условная схема шероховатости соснового шпона, обработанного эластомером
Эластомерная жидкость (резиновая композиция) состоит из длинных цепных молекул, связанных друг с другом в отдельных точках. В результате образуется трехмерная сетка, обладающая единственной формой в ненапряженном состоянии. При оптимальной степени модификации поверхности таким препаратом часть активных центров межмолекулярного взаимодействия блокируется, что ведет к перераспределению напряжений. Это обусловлено тем, что расстояние между центрами, которые взаимодействуют с полимером, увеличивается.
За счет заполнения трещин каучукосодержащим эластомером величина остаточных деформаций уменьшается. Выступы шероховатостей склеиваемой поверхности материала становятся своего рода сжатыми пружинами, которые после снятия давления стремятся восстановить свои первоначальные размеры. Если этому препятствует клеевая прослойка, упругие силы создают остаточные напряжения, действующие перпендикулярно плоскости склеивания.
Наиболее важной задачей такой модификации является уменьшение физико-механической и структурной анизотропии фанеры. Эти изменения в состоянии клееного слоистого композита, каковым является строительная фанера, достигается за счет увеличения ее прочности в направлениях, не совпадающих с направлением волокон. Фанеру принято считать ортотропным материалом, поэтому параметры ее напряженного состояния рассчитывают с использованием элементов теории упругости ортотропного тела. Следовательно, древесина обладает разными механическими свойствами в направлении трех взаимно-перпендикулярных осей: продольной (L) вдоль волокон, радиальной (R) – перпендикулярной к годичным кольцом дерева и тангентальной (т) – касательной к годичным слоям (рис. 2, 3).
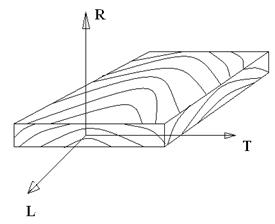
Рисунок 2. Оси направленности векторов по отношению к ориентации волокон и годичных слоев древесины
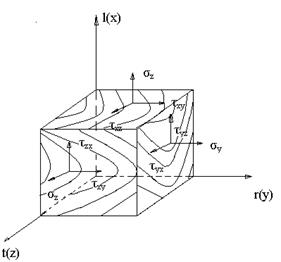
Рисунок 3. Обозначение напряжений при трехосном сжатии образца древесины
Как известно [4], зависимость между величиной деформации и действующей на тело силой выражается законом Гука: деформация упругого тела пропорциональна действующему усилию. Математически эта зависимость для ортотропного материала имеет следующий вид:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
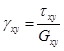 , (4)
, (4) ![]() , (5)
, (5) ![]() (6)
(6)
где σ – нормальное напряжение;
ε – относительная продольная деформация;
Е – модуль упругости;
μ – коэффициент поперечной деформации (коэффициент Пуассона);
τ – касательное напряжение, действующее по площадке с нормалью х параллельно оси у;
G – модуль сдвига.
Существует два вида определения показателей:
1) расчет слоистой клееной конструкции (тела) с взаимно перпендикулярным расположением волокон древесины;
2) расчет напряжений и деформаций в отдельных слоях шпона.
В своих работах Ашкенази Е. Н. и Леонтьев Н. Л. представили формулы упругих постоянных. Оси, определяющие направление векторов напряжений, и определены путем преобразования компонентов деформаций от одних осей к другим [1, 4]. Эти преобразования дают объективную характеристику прочностных и упругих свойств фанеры для расчета индивидуальных свойств слоев шпона. С нашей точки зрения, этот метод более перспективен, поскольку при его применении представляется возможным учесть такие факторы, как пороки и дефекты древесины, существенно влияющие на прочностные и упругие характеристики материала.
В трехмерном пространстве симметрия какого-либо свойства анизотропной сплошной среды может быть изучена путем анализа симметрии геометрической поверхности, изображающей изменение величин, определяющих это свойство при изменении направления в этой среде. Если за оси координат выбрать оси симметрии ортотропного тела х, у, z, то каждая точка характеристической поверхности будет находиться от начала координат на величину радиуса – вектора r, а его проекции на оси координат определяться из выражений:
![]() ,
,
![]() , (7)
, (7)
![]() ,
,
Поворот осей координат определяется схемой косинусов:
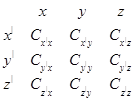 (8)
(8)
В этих математических уравнениях характеристики прочности изменяются в зависимости от поворота осей координат. Но при этом такой фактор влияния как собственно клей, соединяющий слои фанеры между собой, не рассматривается. Вместе с тем экспериментально подтверждено, что однородность поля напряжений и деформаций, а в итоге прочность фанеры зависит не только от угла поворота листов шпона в пакете, но и от характеристик клея. В этой связи любое изменение физико-механических показателей древесины и клея приведет к изменению свойств анизотропности слоистого композита. Если же вводится еще какой либо компонент, например эластомер или органический наполнитель, то эффект проявится еще в большей степени.
Этот метод вполне приемлем для анализа деформативных состояний фанеры, поскольку представляется возможным учитывать такие факторы, как пороки и дефекты древесины, существенно влияющие на прочностные и упругие характеристики материала. Однако он не определяет истинного напряжения в отдельных слоях шпона.
Характеристики и расчетные показатели обосновал и подробно изложил А. Н. Кириллов [2]. Он оценивал свойства отдельных слоев шпона, составляющих пакет, с учетом их числа и взаимно перпендикулярного расположения.
На основе этих данных мы предложили рассматривать фанеру из модифицированного шпона как трехэлементную модель. Одним из компонентов системы является эластомер, которым пропитывается шпон (рис. 4). Если классическая фанера показывается в виде двухэлементной структуры, то исследуемый продукт в зоне клеевого соединения уже представляется составленным из трех компонентов: клея, эластомера и древесины. Идеализированная модель позволяет упростить расчеты и анализ деформационных проявлений. Так как на формирование клеевого соединения и получение монолитного слоистого композита в значительной мере влияют микротрещины, выходящие на контактные поверхности листов шпона, то необходимо оценить это влияние количественно.
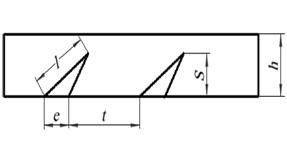
Рисунок 4. Модель пакета СФ из модифицированного соснового шпона
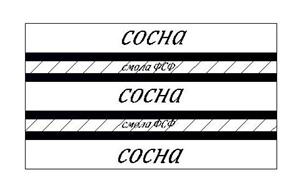
Рисунок 5. Условная шероховатость шпона: S – глубина, е – ширина, t – шаг, h – высота шпона, l – длина.
Величину выступа трещин, характеризующих шероховатость (рис. 4), условно можно определить по формуле (рис. 5): k=eS/2t (9), т.к. шпон у нас обрабатывается с двух сторон, то формулу можно записать в следующем виде: k=eS/t(10).
Представим трехкомпонентный композит в виде конструкции, в которой все слои шпона имеют одинаковую толщину и расположены взаимно перпендикулярно. Общее число слоев композита обозначим условно элементом «С». При нанесении эластомера на поверхность шпона часть вязкого вещества проникает в трещины, на основании чего формулу можно представить как: «с+k». Соответственно толщина шпона будет выражена как «h-k». Итоговая формула определения модуля упругости с учетом направления слоев шпона в композите принимает вид:
![]() ,(11)
,(11)
![]() ,(12)
,(12)
где Е0 ,Е90 – модули упругости с продольным и поперечным расположением волокон лицевого слоя фанеры;
μ0, μ90,μэ – коэффициенты Пуассона шпона вдоль и поперек волокон, эластомера;
n – общее число элементарных слоев;
n0 – общее число продольных слоев, совпадающих с осью: λ= Е90 /Е0 ;
h – толщина шпона;
с – общее число композитных слоев;
Преобразовав формулу получим:
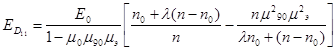 , (13)
, (13)
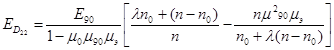 , (14)
, (14)
Формулы (11–14) включают величины упругих констант шпона и клея (Е, μ). Расчет приведенного модуля упругости с учетом влияния клеевых слоев имеет ограниченный характер, так как этот метод применим лишь для фанеры с равной толщиной всех слоев шпона.
На основании исследований, ранее проведенных А. Н. Кирилловым для равнослойной березовой фанеры, можно утверждать, что расчет прочностных характеристик фанеры по элементарному слою позволяет с точностью до 18 % рассчитать аналитическим путем предельные показатели прочности фанеры, в т.ч. и из модифицированного шпона. При этом вводимые в расчетные формулы базовые параметры скорректированы по величинам согласно физико-механическим свойствам эластомера – модификатора, внедренного в поверхностный, контактный слой шпона и по показателям древесины самого шпона. Метод, основанный на оценке свойств отдельных слоев шпона, более точный, а следовательно, дает более объективную характеристику прочностных и упругих свойств фанеры в целом.
Рецензенты:
Сарапулов С. Ф., доктор технических наук, профессор, заместитель Министра промышленности и науки Свердловской области, Министерство промышленности и науки Свердловской области, г. Екатеринбург.
Глухих В. В., доктор технических наук, профессор, Уральский государственный лесотехнический университет, г. Екатеринбург.



