Введение
Все манипуляторные машины, используемые в лесной промышленности на погрузочно-разгрузочных, технологических и вспомогательных операциях, можно разделить на три группы [1- 5].
1. Погрузчики-штабелеры. Под этими механизмами понимаются самоходные машины с краном-манипулятором, предназначенные для штабелевки, погрузки и выгрузки круглых лесоматериалов.
2. Навесные манипуляторы. Это манипуляторы, монтирующиеся на различные механизмы и транспортные средства без значительных изменений конструкции последних и имеющие основным целевым назначением обслуживание этих механизмов и транспортных средств или совместную работу с ними. При демонтаже манипулятора база может использоваться по своему прямому назначению.
3. Технологические манипуляторы. Это манипуляторные механизмы стационарного или передвижного типа, используемые в качестве околостаночного оборудования, а также оборудования технологических линий лесных складов, лесоперевалочных баз, бирж сырья, лесоперерабатывающих цехов и т.д.
Решение задачи обоснования и выбора типа манипулятора невозможно без кинематического анализа различных его модификаций.
В настоящей работе поставлена задача определения линейных характеристик точек звеньев манипулятора в зависимости от времени.
Расчет кинематических характеристик
В общем случае с учетом деформируемости звеньев манипулятора система имеет бесконечное множество степеней свободы. Создание математической модели потребует составления огромного числа уравнений. Ограничить число степеней свободы можно, приняв все звенья абсолютно твердыми [4].
Переход от технического объекта к расчетной схеме изображен на рис. 1, где не показаны гидроцилиндры, стойка и другие, незначительные для исследования кинематики звенья. Вращения стойки и стрелы относительно стойки обеспечены сферическим шарниром в точке О. Плоскость, содержащая стрелу и рукоять, поворачивается вокруг оси Z, благодаря этому шарниру. На основе расчетной схемы построена математическая модель, исследование которой проведено с использованием программного комплекса MAPLE 9.5.
Получим соотношения для кинематических характеристик точки B. Примем в качестве первого приближения: угол между стрелой и рукоятью постоянный, l1 –длина стрелы и l2 –длина рукояти – не меняются. Обозначим угол между стрелой и рукоятью как ψ (рис. 1).
Пусть все звенья манипулятора являются абсолютно твердыми. В этом случае для груза B манипулятор будет являться голономной связью. Поскольку координаты точки B зависят от времени, то эта связь будет нестационарной. Будем считать ее идеальной, т.е. работой всех реакций на заданных возможных перемещениях системы пренебрегаем. Расстояние между точками O и B остается постоянным при неизменном угле ψ. Отрезок OB наклонен к плоскости под углом γ. Пусть угол поворота вокруг стойки обозначен как θ. Перемещения манипулятора – это изменения угла γ и угла поворота вокруг стойки θ.
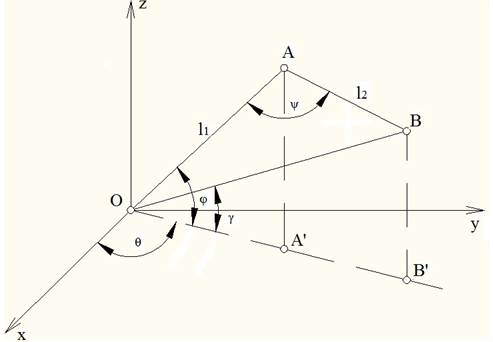
Рис. 1. Расчетная схема.
На расчетной схеме имеем: О – точка крепления стрелы к стойке; А – шарнир между рукоятью и стрелой; В – точка подвеса груза; θ, φ, γ – углы, определяющие положение звеньев. Имеем две переменные величины, являющиеся функциями по времени: θ = f1(t), γ = f2(t).
Параметрические уравнения движения точки B в декартовой системе координат представляют собой зависимости:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
где высота Н – высота стойки. В данном случае будем считать ее равной 0. Из треугольника ОАВ определим ОВ, как
![]() . (4)
. (4)
Из уравнений (1-3) определим скорость точки В.
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() . (7)
. (7)
Здесь приняты следующие обозначения 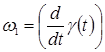 – угловая скорость вращения стрелы (γ') в вертикальной плоскости,
– угловая скорость вращения стрелы (γ') в вертикальной плоскости, 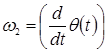 – угловая скорость поворота вокруг стойки (θ'). Абсолютная скорость точки В получается в виде:
– угловая скорость поворота вокруг стойки (θ'). Абсолютная скорость точки В получается в виде:
![]() . (8)
. (8)
Дифференцируя формулы (5), (6) и (7) по времени, получим ускорение точки В относительно осей X, Y, Z:
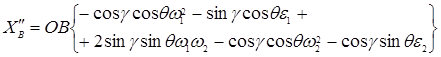 . (9)
. (9)
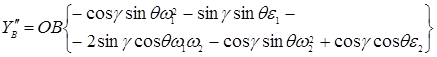 . (10)
. (10)
![]() . (11)
. (11)
Здесь приняты следующие обозначения 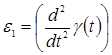 – угловое ускорение вращения стрелы (γ'') в вертикальной плоскости,
– угловое ускорение вращения стрелы (γ'') в вертикальной плоскости, 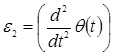 – угловое ускорение поворота вокруг стойки (θ''). Абсолютное ускорение точки В:
– угловое ускорение поворота вокруг стойки (θ''). Абсолютное ускорение точки В:
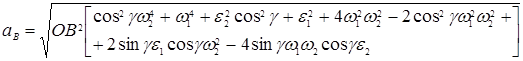 . (12)
. (12)
Результаты
Для анализа результатов используем компьютерную программу MAPLE 9.5.
Построим графики зависимости линейной скорости движения точки В подвеса груза от времени и угловой скорости в вертикальной плоскости![]() .
.
Пусть угловая скорость в горизонтальной плоскости постоянна. Таким образом, будем рассматривать установившееся движение по горизонтали и переменное движение манипулятора в вертикальной плоскости. В качестве начальных условий выбираем значения длины плеча подвеса груза ОВ = 3 м, 6 м. В интервале времени t от 0 до 5 секунд и при переменной угловой скорости ![]() в интервале от 0 до 0,5 рад/с построим графики скорости точки подвеса груза. Построение выполним для разных значений длины ОВ (для разных значений угла ψ). Чем больше угол, тем больше расстояние ОВ, тем больше линейная скорость груза. Результат приведен на рисунке 2.
в интервале от 0 до 0,5 рад/с построим графики скорости точки подвеса груза. Построение выполним для разных значений длины ОВ (для разных значений угла ψ). Чем больше угол, тем больше расстояние ОВ, тем больше линейная скорость груза. Результат приведен на рисунке 2.
а)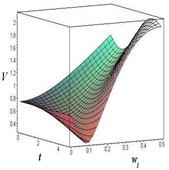 б)
б)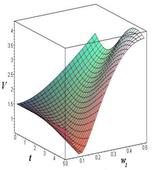 в)
в)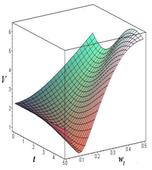 г)
г)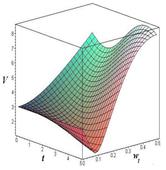
Рис. 2. Зависимость линейной скорости от времени и угловой скорости при разных значениях параметра ОВ: а) – ОВ = 3 м; б) – ОВ = 6 м; в) – ОВ = 9 м; г) – ОВ =12 м.
Зависимость скорости груза от времени и ![]() для разных значений
для разных значений ![]() показаны на рисунках 3. На рисунке 3 длина ОВ взята равной 3 м, на рисунке 4 – 6 м.
показаны на рисунках 3. На рисунке 3 длина ОВ взята равной 3 м, на рисунке 4 – 6 м.
а)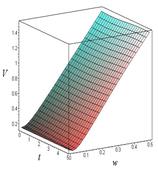 б)
б)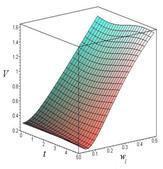 в)
в)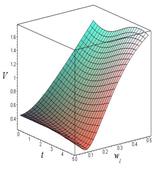 г)
г)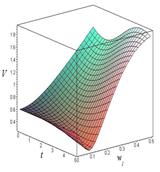
Рис. 3. Зависимость линейной скорости от времени и угловой скорости при ОВ = 3 м:
а) – ![]() рад/с; б) –
рад/с; б) – ![]() рад/с; в) –
рад/с; в) – ![]() рад/с; г) –
рад/с; г) – ![]() рад/с.
рад/с.
а)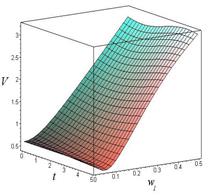 б)
б)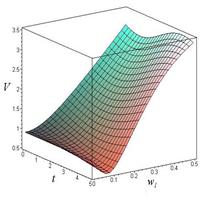 в)
в)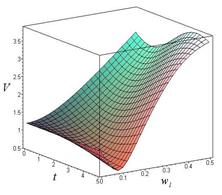
Рис. 4. Зависимость линейной скорости от времени и угловой скорости при ОВ = 6 м:
а) – ![]() рад/с; б) –
рад/с; б) – ![]() рад/с; в) –
рад/с; в) – ![]() рад/с.
рад/с.
Обсуждение результатов
Обзор графиков выявил ряд особенностей.
1. Чем больше угол между стрелой и рукоятью, тем больше скорость груза. Например, для ![]() = 0,5 рад/с скорость VB =2 м/с для ОВ=3 м, а для ОВ=12 м величина скорости может достигать 8 м/с (рис. 2). Характер зависимости остается примерно одинаковым.
= 0,5 рад/с скорость VB =2 м/с для ОВ=3 м, а для ОВ=12 м величина скорости может достигать 8 м/с (рис. 2). Характер зависимости остается примерно одинаковым.
2. График скорости представлен прямой линией параллельной оси t при угловой скорости ![]() рад/с (угол наклона стрелы к горизонтальной плоскости
рад/с (угол наклона стрелы к горизонтальной плоскости ![]() постоянен), что является очевидным, так как из формулы (8) следует, что
постоянен), что является очевидным, так как из формулы (8) следует, что ![]() , (рисунок 5а).
, (рисунок 5а).
а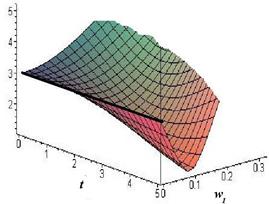 б
б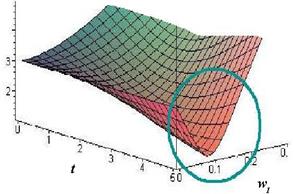
Рис. 5: а - скорость при ![]() зависит от длины ОВ и подчиняется закону
зависит от длины ОВ и подчиняется закону ![]() ;
;
б - зависимость линейной скорости от времени и угловой скорости при ![]() рад/с, ОВ = 3 м.
рад/с, ОВ = 3 м.
3. Независимо от длины ОВ существует минимум линейной скорости при ![]() рад/с. Например, на рисунке 5б показан минимум скорости при вращении вокруг вертикальной оси 0,1 рад/с и расстоянии ОВ, равном 3 м.
рад/с. Например, на рисунке 5б показан минимум скорости при вращении вокруг вертикальной оси 0,1 рад/с и расстоянии ОВ, равном 3 м.
4. Чем больше ![]() , тем больше отклонение от линейной зависимости скорости (рис. 3).
, тем больше отклонение от линейной зависимости скорости (рис. 3).
Анализируя графики, можно сказать, что для увеличения производительности работы манипулятора при установившейся постоянной угловой скорости в горизонтальной плоскости следует быстрее перескакивать диапазон вертикальных угловых скоростей от 0 до 0,2 рад/с в вертикальной плоскости.
Линейная скорость VB растет пропорционально увеличению длины ОВ. Наиболее производительный интервал скоростей находится между ![]() рад/с. Во избежание значительных динамических нагрузок следует не превышать скорость
рад/с. Во избежание значительных динамических нагрузок следует не превышать скорость ![]() рад/с.
рад/с.
Рецензенты:
Ляпцев Сергей Андреевич, профессор, доктор технических наук, зав. кафедрой технической механики УГГУ, Уральский государственный горный университет, г. Екатеринбург.
Ковалев Рудольф Николаевич, профессор, доктор технических наук. зав. кафедрой экономики транспорта и логистики, Уральский государственный лесотехнический университет, г. Екатеринбург.



