Введение
Разработка рыбохозяйственной САПР – необходимое условие для успешного функционирования рыбохозяйственного комплекса, особенно в современных условиях агрессивного промысла гидробионтов [1]. Постоянное истощение промысловых запасов является определяющим фактором в разработке подсистемы автоматизированного проектирования орудий лова (ОЛ), которые приспособлены для селективного лова и обеспечивают оптимальный режим промысла. Проблемы создания эффективных рыбохозяйственных САПР неоднократно обсуждались [5, 6]. Известны зарубежные и отечественные САПР РХ объектов – Ashlar Vellum Graphite, Trawl Design, Otterboard, Trawl Cad, а на определенных этапах проектирования для построения параметрических моделей деталей используются SALOME, Medusa4, Wings 3D и подобные им системы [5]. Однако указанные системы имеют ряд ограничений: 1) ориентированы на узкий круг специалистов высокого уровня подготовки; 2) являются коммерческими системами с программными модулями, закрытыми для модификации; 3) лингвистическое обеспечение не предоставляет возможности их тонкой настройки; 4) не позволяют учитывать поведение гидробионтов, поэтому оптимизация параметров ОЛ проводится проектировщиками эмпирически по результатам дорогостоящих и многоэтапных натурных испытаний прототипа. Таким образом, известные рыбохозяйственные САПР не в полной мере отвечают потребностям рыбодобывающей отрасли. В данной работе представлено краткое описание программного и математического обеспечения САПР орудий лова «Trap» и приведена типовая задача оптимизации параметров крабовой ловушки.
Программное обеспечение САПР. Потребности рыбохозяйственного комплекса диктуют ряд общесистемных принципов разработки САПР ОЛ: проектирующие подсистемы должны использовать дружественный пользовательский интерфейс с функцией графической визуализации результатов проектирования; в основу системы должна быть положена единая база данных (БД), обеспечивающая информационную поддержку проектных процедур на всех этапах проектирования; система должна быть открыта для включения в нее внешних программных модулей, предназначенных для решения новых проектных задач.
На рис. 1 показана каркасная архитектура программного обеспечения (ПО) системы «Trap», разработанная согласно общесистемным требованиям [2]. Особенностью организации ПО системы следует считать разделение инструментальной (диалоговое ПО) и исполнительной (проблемной) частей. В САПР "Trap" диалоговое ядро отвечает за поддержку информационных связей между компонентами системы и обеспечивает комфортное диалоговое взаимодействие с проектировщиком, в то время как проблемное ПО ориентировано на решение задач проектирования ОЛ.
Проблемная часть системы позволяет проводить анализ размерно-полового состава улова 12, для выявления доли молоди и самок в улове; параметрическую оптимизацию конструкции ОЛ 14; матричные и комплексные вычисления 11. Состав средств ПО «Trap» позволяет замкнуть задачу принятия проектных решений в условиях неопределенности, обусловленной многокритериальностью.
Математическое обеспечение САПР. Разработка проектирующих подсистем опирается на исследования [1, 2, 6] и моделирование [3] процесса лова, включая механизм пространственного поведения гидробионтов в зависимости от наблюдаемой ими окружающей среды. В состав математического обеспечения системы «Trap»
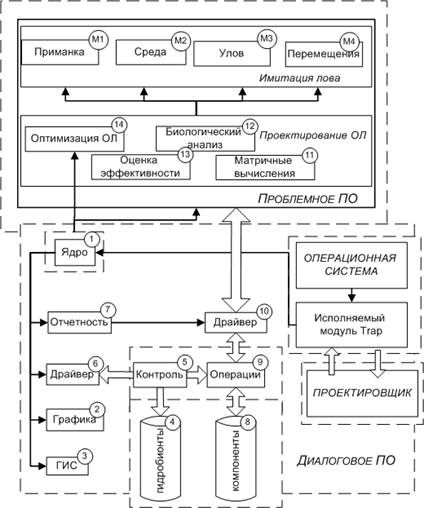
Рис. 1. Архитектура ПО системы "Trap"
включены четыре математические модели процесса лова промысловых гидробионтов: модели М1, с помощью которой имитируется распространение шлейфа запаха от приманки в морской среде; модели М2, предназначенной для имитации гидродинамических свойств морской среды; модели М3, предназначенной для имитации попадания гидробионтов в ловушку; модели М4, предназначенной для имитации пространственного поведения гидробионтов в процессе поиска пищи.
Модель М1. Применение краевой задачи вида (1) является традиционным для изучения поведения пассивных взвесей в воздухе и воде [3]. Решение задачи (1) для произвольной функции f(t) можно описать в виде объёмного потенциала от функции влияния и функции источника:
![]() , (2)
, (2)
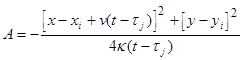 , где
, где ![]() = jDt, j = 0, 1, …, T - 1.
= jDt, j = 0, 1, …, T - 1.
При тестировании модельного шлейфа запаха использовались следующие значения параметров модели: κ = 10−4 м2 / с, |v| = 5´10−2 м / с, ![]() = 0 г / с, Q = 100 г, ac = 10−7 г / м3, Tb = Tsoak = 53 ч., Dt = 1 ч.; полученные в результате имитации параметры шлейфа сверялись с опубликованными контрольными значениями. Результат тестирования модели распространения шлейфа, выполненной с применением формулы (2), показан в таблице 1.
= 0 г / с, Q = 100 г, ac = 10−7 г / м3, Tb = Tsoak = 53 ч., Dt = 1 ч.; полученные в результате имитации параметры шлейфа сверялись с опубликованными контрольными значениями. Результат тестирования модели распространения шлейфа, выполненной с применением формулы (2), показан в таблице 1.
Таблица 1
|
|
Протяжённость шлейфа, км, |
Максимальная ширина, км |
Площадь, кв. км |
|
Результаты модели |
9,50 |
0,33 |
1,95 |
|
Контрольные значения |
8,37 |
0,33 |
2,00 |
|
Различие |
2,5% |
0% |
11,9% |
Модель М2 получена на основе краевой задачи [5]: ![]() , (1)
, (1)
![]() , t > 0;
, t > 0; ![]() ,
, ![]() ,
, ![]() , i = 1, 2, …, M, t > 0,
, i = 1, 2, …, M, t > 0,
где r – радиус-вектор координат на плоскости ![]() ; r = (x, y);
; r = (x, y); ![]() – радиус-вектор координат i-й ловушки, i = 1, 2, …, M – номера ловушек в порядке;
– радиус-вектор координат i-й ловушки, i = 1, 2, …, M – номера ловушек в порядке; ![]() – концентрация аттрактанта в точке с радиус-вектором координат r в момент времени t; κ – коэффициент горизонтальной турбулентной диффузии; v – вектор скорости течения;
– концентрация аттрактанта в точке с радиус-вектором координат r в момент времени t; κ – коэффициент горизонтальной турбулентной диффузии; v – вектор скорости течения; ![]() – коэффициент поглощения аттрактанта в морской воде.
– коэффициент поглощения аттрактанта в морской воде.
Модель М3. Экспериментальные исследования [1] выявили существование зависимости величины улова от конструкции сетной поверхности ОЛ. К примеру, при превышении шага ячеи сетной поверхности отметки 165 мм, улов падает до нуля. Сетная часть ловушки представляет собой прямоугольную сетную пластину. Пример раскроя сетной части показан на рис. 2.
Для углов раскрытия ячей сетной оболочки верно рекуррентное соотношение ![]() где
где ![]() – центральный угол, охватывающий один ряд ячей, т.е. каждая последующая ячея суживается по ширине сетной оболочки на величину
– центральный угол, охватывающий один ряд ячей, т.е. каждая последующая ячея суживается по ширине сетной оболочки на величину ![]() относительно предыдущей. Число ячей по ширине i-й части сетной пластины для покрытия каркаса определяется выражением
относительно предыдущей. Число ячей по ширине i-й части сетной пластины для покрытия каркаса определяется выражением ![]() , i = 1, 2, 3, где
, i = 1, 2, 3, где ![]() – углы
– углы
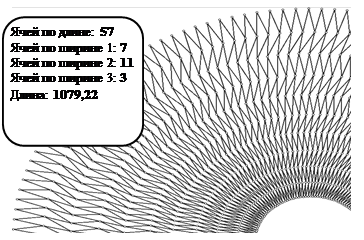
Рис. 2. Пример раскроя сетной конструкции ОЛ
раскрытия ячей по нижней и верхней кромкам соответственно. Для верха и низа ![]() =
= ![]() =
= ![]() , для бока
, для бока ![]() , где
, где ![]() – длина образующей конуса ловушки. Коэффициент посадки дели на нижнее кольцо каркаса задано выражением
– длина образующей конуса ловушки. Коэффициент посадки дели на нижнее кольцо каркаса задано выражением ![]() = 0,7 – 0,9. Число ячей по длине сетной пластины определяется как
= 0,7 – 0,9. Число ячей по длине сетной пластины определяется как ![]() . Длина пластины в жгуте может быть найдена по формуле
. Длина пластины в жгуте может быть найдена по формуле ![]() . Число ячей по ширине i-й части сетной пластины можно определять по формуле Баранова [1]
. Число ячей по ширине i-й части сетной пластины можно определять по формуле Баранова [1] ![]() , где
, где ![]() – ширина в посадке i-й части сетной пластины.
– ширина в посадке i-й части сетной пластины. ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – длина образующей конуса ловушки.
– длина образующей конуса ловушки.
Модель М4. В поисках пищи донные гидробионты исследуют территорию, совершая случайные перемещения по дну, пока не обнаружат привлекающий запах. Контактируя со шлейфом запаха, животные изменяют случайное блуждание на целенаправленную миграцию к источнику запаха [3]. Поиск источника запаха донными животными через контакт со шлейфом математически формализован в виде стохастических уравнений: ![]() , где:
, где: ![]() – координаты особи с индексом k в момент времени t; k = 1, 2, …, N; t = 1, 2, …, T;
– координаты особи с индексом k в момент времени t; k = 1, 2, …, N; t = 1, 2, …, T; ![]() – безразмерный единичный вектор движения:
– безразмерный единичный вектор движения: ![]() – шаг по времени при расчете движения особи.
– шаг по времени при расчете движения особи.
Задача параметрической оптимизации ОЛ в общем случае может быть сформулирована в классическом виде
GP(P)àextr, PÎD
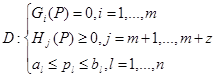 ,
,
где Gp(P) – векторная функция цели, P = {p1, p2, p3,…,pn} – вектор варьируемых параметров, Gi(P) = 0, i = 1,…, m, – функциональные ограничения равенства, Hj(X) ≥ 0, i = m + 1,…, m+z - функциональные ограничения неравенства, al и bl – компоненты векторов, представляющих собой верхние и нижние границы вариации вектора P. Основными параметрами конструкции, влияющими на эффективность крабовых ловушек, являются: габаритные характеристики – диаметр нижнего и верхнего оснований d1,2осн, высота H, угол конусности ловушки β; количество входных устройств Nвх; диаметры входов Dk, k = 1, 2, ..., Nвх; высоты расположения входов hk, k = 1, 2, ..., Nвх и расстояния между ними rkl, k,l = 1, 2, ..., Nвх, k ≠ l; Характерной трудностью задач оптимизации ОЛ является большое количество и разнообразие параметров. На практике, чтобы снизить размерность задачи, выбирают только основные варьируемые параметры, либо объединяют группы параметров в интегральные показатели [1]. К примеру, количество и диаметры входов следует выражать через суммарную площадь входных устройств по формуле ![]() .
.
Методы решения данного класса задач векторной оптимизации подразумевает применение оптимизационных алгоритмов первого и второго порядка, а также генетических поисковых стратегий [4]. Стратегия поиска оптимальных проектных решений основана на итерационной схеме и использует свойства программно реализованных алгоритмов: 1) запускается генетический алгоритм; 2) осуществляется выбор опорной точки поискового пространства, соответствующей конструкции ОЛ; 3) проводится серия имитаций процесса лова полученной конструкцией; 4) рассчитывается эффективность полученного ОЛ.
Практическое решение типовой задачи. В качестве иллюстрации проектной задачи была проведена оптимизация параметров существующей конструкции конусной крабовой ловушки с целью максимизации ее эффективности. Критерием эффективности выступает целевая функция, представленная в виде зависимости от улова ловушки Q и радиуса зоны облова rЗО: gP(P) = wQ Q +wr rЗО, wQ + wr = 1. Q и rЗО являются функциями от вектора варьируемых параметров P = {d1,2осн, H, β, Nвх, Dk, hk, rkl} при k,l = 1, 2, ..., Nвх, k ≠ l, который состоит из габаритных параметров ловушки. Требования заказчика, указанные в проектной документации, накладывают определенные ограничения на конструкцию ловушки: число входов должно быть не более четырех, а объем ловушки должен быть рассчитан не более чем на 17 особей. Тогда задача оптимизации формулируется следующим образом gP(P*) = max gP(P) при Nвх ≤ 4 и Q ≤ 17.
При проведении имитаций ловушки в количестве 100 шт. располагали в линейный порядок через 15 м друг от друга. Варьировались значения скорости течения от 0 до 20 см/с при различных типах распределения животных – от равномерного случайного до пятнистого случайного числом от 1 до 10 тыс. экз. на площади 1.6x104 кв. м. Максимизация функции цели привела к уменьшению угла конусности ловушки (до 60 градусов) и увеличению числа входных устройств (с двух до трех). Малый улов при начальном приближении вектора P можно объяснить тем, что в процессе имитации лова многие особи уходили через боковой вход. В итоге подобрано меньшее значение угла наклона и диаметра бокового входа, что в итоге привело к улучшению эффективности ловушки (таблица 2).
В заключение отметим следующее: 1) разработанная система «Trap» предоставляет проектировщику средства для принятия проектных решения в условиях неопределенности за счет гибкости диалогового взаимодействия; 2) математическое обеспечение системы является проблемно-инвариантным; 3) система «Trap» была апробирована сотрудниками СахНИРО на этапе имитационного моделирования процесса лова.
Рецензенты:
Скобельцын К. Б., д-р техн. наук, профессор кафедры системного анализа и управления СПб. государственного политехнического университета, г. Санкт-Петербург.
Куприянов М. С., д-р техн. наук, декан факультета компьютерных технологий и информатики СПб. государственного электротехнического университета "ЛЭТИ", г. Санкт-Петербург.



