В подготовке будущих специалистов большую роль играет аналитико-синтетическая компетентность, которая составляет основу когнитивной (познавательной) и социально-профессиональной компетентностей [5].
Для развития аналитико-синтетической компетентности обучающихся политехнического техникума мною были определены теоретические основы развития указанной компетентности, выявлены возможные пути и средства для ее развития.
Формирование аналитико-синтетической компетентности у обучающихся должно быть связано с актуальным для них предметным материалом.
Сегодня элементы теории вероятностей и математической статистики становятся важным компонентом общего образования современного человека и являются материальным инструментарием для описания явлений и процессов реальной действительности [2]. Решая задачи по данному курсу, обучающиеся учатся решать организационно-управленческие задачи, которые касаются вопросов, связанных с использованием математического аппарата в процессе подготовки производственных отчетов, принятия управленческих решений. Мы привыкли к тому, что любой «письменный» предмет преподается со всеми присущими ему чертами: серьезность, догматизм, многократный повтор одних и тех же алгоритмов. А на уроках по теории вероятностей и математической статистике надо решить несколько задач, абсолютно непохожих друг на друга. Задачи, стоящие в учебнике рядом, не аналогичны, решение одной из них не означает, что будет с легкостью решена следующая [1]. Проведя анализ учебной, методической, научно-методической литературы, мы можем сделать вывод, что имеющееся учебное обеспечение дисциплины «Теория вероятностей и математическая статистика» в целом способствует организации целенаправленной работы по развитию у студентов аналитико-синтетической компетентности.
В результате исследования мы пришли к заключению, что помимо «традиционных» задач по теории вероятностей и математической статистике, способствующих формированию аналитико-синтетической компетентности, нужно прибегнуть к помощи «нетрадиционных» задач.
Существует такой класс задач, которые не укладываются в традиционную классификацию. Это задачи стратегического характера. Задачи данного типа в своей работе выделила И.Г. Диченко [3].
Стратегическая задача – это игровая ситуация, для которой можно просчитать выигрышную стратегию, т.е. гарантирующую победу за конечное число ходов при любых соображениях противника. В первую очередь необходимо уяснить, что стратегическая задача заключается в том, чтобы рассчитать все возможные ходы противника, и на каждый его ход найти правильную игру [3].
Среди задач стратегического характера И.Г. Диченко [3] выделяет следующие типы:
– задачи на симметричную стратегию;
– задачи на парную стратегию;
– задачи на стратегию непрерывной угрозы;
– задачи на стратегию построения числовой последовательности;
– задачи на комбинированные стратегии.
Стратегические задачи всегда относились к разделу занимательной математики. Как правило, ученики не могут решать задачи стратегического характера, выходящие за рамки привычных алгоритмов, даже если для их решения не нужны дополнительные знания. Решение таких задач требует интеграции знаний из различных образовательных областей, конструирования новых способов аргументации, опровержения гипотез, прогнозирования результатов, планирования исполнения, коррекции, оценки [3]. Следовательно, стратегические задачи могут помочь в формировании аналитико-синтетической компетентности.
К задачам стратегического характера относят и математические игры. Успешное участие в игре должно быть продумано заранее, т.е. должна быть выбрана беспроигрышная стратегия или алгоритм. В.Н. Касаткин [6] предлагает разнообразные математические игры, связанные с серьезными научными теориями. Рассматривая данные игры, мы предлагаем найти вероятность выигрыша в той или иной игре.
Задача 1. Игра Болтянского. Играют двое. Первый называет натуральное число от 2 до 9; второй умножает это число на произвольное натуральное число от 2 до 9. Затем первый умножает результат на любое натуральное число от 2 до 9 и т.д. Выигрывает тот, у кого раньше получится произведение, превышающее: а) тысячу; б) миллион. Какова вероятность, что это будет второй игрок?
Задача 2. Игра «На дорожке». Играют двое. На концах дорожки, разбитой на М клеток, стоят две разноцветные фишки (рис. 1). Противники ходят поочередно. Сделать ход – значит продвинуть свою фишку не более, чем на К клеток вперед или назад, не перескакивая через фишку противника и не выходя за пределы дорожки.
Победителем считается тот, кто сделает последний ход. Какова вероятность, что это будет второй игрок?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 1.
При решении задач такого характера для поиска выигрышной стратегии следует выполнить следующие действия:
1. Проанализировать несколько частных случаев решения задачи.
2. Выдвинуть гипотезу выигрышной стратегии.
3. Обосновать правильность выигрышной стратегии.
При решении задачи стратегического характера требуется комплексное применение таких мыслительных операций, как анализ, синтез и предвидение.
Основными идеями решения таких задач являются [4]:
1. Решение с конца. Последовательно определяются позиции, выигрышные и проигрышные для начинающего. Выигрышными позициями, определенными на очередном шаге, являются те, из которых можно получить ранее определенную проигрышную позицию.
· Используется в играх при анализе выигрышных и проигрышных ситуаций.
· Предполагают, что требуемое верно, и идут от него к исходным данным.
2. Соответствие. Наличие удачного ответного хода может обеспечиваться симметрией, разбиением на пары.
3. Передача хода. Если мы пользуемся стратегией противника, то наши дела не хуже, чем у него. Например, выигрыш (или ничья) обеспечивается, когда можно по своему желанию попасть в некоторую позицию, которая выигрышна для противника.
При решении задачи студенты разрабатывают стратегию ее решения, выдвигают и доказывают гипотезы опытным путем, прогнозируют результаты своей деятельности, анализируют и находят рациональные способы решения задачи путем оптимизации, детализации созданного алгоритма.
Для решения задач стратегического характера был предложен алгоритм, изображенный на рисунке 2.
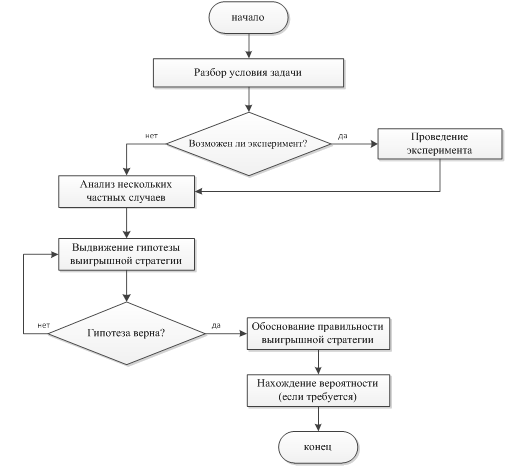
Рис. 2. Схема алгоритма поиска решения задач стратегического характера
Рассмотрим данную схему подробнее.
При разборе условия задачи следует внимательно его прочитать, чтобы правильно понять – что именно требуется получить в качестве решения задачи. Если условие задачи неверно понято, то это может привести к тому, что будет решаться совершенно другая задача, а не та, что сформулирована в условии. В условии задачи ценна каждая фраза, каждое предложение, часто в них прямо или косвенно содержится важная информация.
После разбора условия задачи мы ставим перед собой вопрос: возможно ли провести эксперимент? Т.е. для наглядности проиграть ситуацию. Эксперимент проводится как при помощи подручных средств, так и, если это возможно, с использованием персонального компьютера.
Если эксперимент возможен, то его проводят и делают соответствующие выводы.
После проведения (или не проведения) эксперимента выполняется анализ нескольких частных случаев. В зависимости от условия задачи рассматриваются частные случаи, в которых используются небольшие числа.
На основании эксперимента и проведенного анализа выдвигается гипотеза выигрышной стратегии.
Если гипотеза верна, то проводится обоснование правильности выигрышной стратегии. В противном случае выдвигается новая гипотеза.
Если требуется в задаче, то в заключение решения находят вероятность, применяя соответствующие формулы.
Рассмотрим задачи, которые предлагались студентам во время проведения эксперимента, на применение схемы поиска решения задач стратегического характера.
Задача 1. Ищем выигрышную стратегию.
Имеется фишка и дорожка, разбитая на 15 клеток (рис. 3). Играют двое. Ходят поочередно. Первый игрок ставит фишку на 1-ю, или на 2-ю, или на 3-ю клетку. Каждый игрок во время своего хода передвигает фишку на 1, или на 2, или на 3 клеточки. Проигрывает тот, кто первый достигнет голодного поджидающего Дракона в клетке 15. Знаете ли Вы, как одержать победу в этой игре?
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Рис. 3
При решении данной задачи воспользуемся предложенным алгоритмом.
1. Разбор условия задачи. Дана дорожка, разбитая на 15 клеток, играют 2 игрока, ходят по очереди. За каждый ход игрок может передвинуть фишку на одну, две или три клетки. Требуется выяснить – как одержать победу в игре, если проигрывает тот, кто первый достигнет 15-й клетки.
2. Возможен ли эксперимент? В данной задаче эксперимент возможен, так как имеем дело с конечной, не очень большой последовательностью чисел (от 1 до 15), которую легко изобразить графически.
3. Проведение эксперимента. Проигрывается ситуация.
4. Так как в данной задаче используются небольшие числа, то частных случаев нет.
5. Выдвижение гипотезы выигрышной стратегии. Чтобы соперник оказался на последней клетке, в ваш ход вы должны поставить фишку на 14. До этого ваш ход – 10, чтобы затем поставить фишку на 14 и так далее. Максимум ход – 3 клетки, минимум – 1. Т.е. промежуток должен составлять 3+1=4 клетки.
Нужно стараться, чтобы ваши ходы были на этих клетках: 2 - 6 - 10 - 14.
6. Гипотеза верна? Данная гипотеза верна в том случае, если вы ходите первым. Другое дело, если первым ходит соперник. Но, опять же, победа ваша, если он не знает стратегии игры. Вряд ли может так сильно повезти, что он попадет на все 4 указанные клетки.
7. В данной задаче вероятность находить не требуется.
Задача 2. Игра «Шашки по кругу». Играют двое, ходят поочередно. Сделать ход – это значит взять любые одну или две соседних шашки из нескольких, расположенных рядом по кругу. Победителем считается тот, кто сумеет взять последнюю шашку. Докажите, что это будет игрок, всегда начинающий игру вторым?
Решение.
1. Разбор условия задачи. Имеем N шашек, расположенных по кругу. Играют 2 игрока, ходят по очереди. За каждый ход игрок может взять любые одну или две соседние шашки из нескольких, расположенных рядом по кругу. Требуется доказать, что выигрывает игрок, всегда начинающий игру вторым, если победителем считается тот, кто сумеет взять последнюю шашку.
2. Возможен ли эксперимент? Эксперимент проводился с небольшим количеством шашек (стандартный набор – 24 шашки).
3. Проведение эксперимента. Проигрывается ситуация.
4. Анализ частных случаев. В данной задаче частными случаями являются следующие:
- игрок берет одну шашку;
- игрок берет две шашки.
После любого первого хода круг из N шашек окажется разорванным, и играющие будут иметь дело с «цепочкой» из N1 = N-Р1 шашек.
Если соперник, вступивший в игру первым, оставил цепочку из нечетного числа шашек, то второй игрок должен взять одну, среднюю шашку, образовав две короткие и равные по количеству шашек цепочки ![]() .
.
Если соперник, начавший игру первым, после своего хода оставил цепочку, состоящую из четного числа шашек, то второй игрок должен взять две, средние шашки, образовав две короткие цепочки с одинаковым числом шашек в каждой: ![]() .
.
5. Выдвижение гипотезы выигрышной стратегии. Как бы ни действовал первый игрок (брал одну или две шашки), второму игроку следует сохранять в расположении шашек центральную симметрию (при выполнении хода обращается к симметричной цепочке и берет в ней столько же шашек и так же расположенных, как сделал это его соперник в симметричной цепочке).
6. Гипотеза верна? Данная гипотеза верна в том случае, если вы будете игроком, который ходит вторым.
7. Обоснование правильности выигрышной стратегии. В процессе игры количество цепочек будет увеличиваться, но каждый раз возникает возможность второму игроку восстановить центральную симметрию в расположении оставшихся шашек. Победителем всегда оказывается тот из соперников, кто вступает в игру вторым, начинающий поединок всегда проигрывает. Что и требовалось доказать.
В заключение можно сделать вывод, что решая стратегические задачи, студенты комплексно применяют такие мыслительные операции, как анализ, синтез и предвидение, которые лежат в основе аналитико-синтетической компетентности.
Применение стратегических задач для формирования аналитико-синтетической компетентности обусловлено еще и тем, что можно использовать такой вид наглядности, как экспериментальная наглядность, тот есть можно проводить небольшие эксперименты, а если мы имеем дело с большими числами, то ситуацию можно смоделировать на компьютере.
Рецензенты:
Ведерникова Л.В., д.п.н., профессор, проректор по научной и инновационной деятельности ФГБОУ ВПО «ИГПИ им. П.П. Ершова», г. Ишим.
Далингер В.А., д.п.н., профессор, заведующий кафедрой теории и методики обучения математике ФГБОУ ВПО «ОмГПУ», г. Омск.




