Введение
Одним из факторов эффективной ультразвуковой окорки лесоматериалов являются показатели кавитационного эффекта, возникающего в области действия ультразвука. В связи с этим необходимо разработать комплексную модель возникновения кавитационного эффекта с параметрированием показателей возникающей при этом энергии.
Кавитационный эффект, возникающий в зоне разрушения элементов и слоёв коры, можно условно дифференцировать на два этапа: возникновение и динамика; рост и схлопывание кавитационного пузырька. Так как процесс ультразвуковой окорки происходит в водной среде, то при возникновении и динамике каверны формируются гидродинамические течения, а при схлопывании выделяется энергия, разрушающая слои коры [1].
Цель исследования
Целью исследований является математическое моделирование кавитационного эффекта, происходящего на границах коры и способствующего элементному разрушению коры деревьев.
Материалы и методы исследования
Исследования акустической кавитации позволяют получать наиболее адекватные результаты по воспроизводимости условий эксперимента, а также дают возможность проведения измерений физических параметров в кавитационной области. Заметим, что близкие по природе физико-химические эффекты имеют место и при целом ряде воздействий другой физической природы, таких как лазерная кавитация, гидродинамическая кавитация, электрогидравлический взрыв, ударное механическое воздействие на взвесь пузырьков в жидкости и т.п. Тем не менее, устоявшаяся акустическая терминология широко используется и в настоящее время, поэтому в работе также использовались эти общепринятые термины.
В частотном диапазоне 25–50 кГц, при котором реализуется ультразвуковая окорка лесоматериалов, используются магнитострикционные излучатели, работающие в резонансном режиме. Этому способствуют оптимальные с точки зрения конструкций излучателей геометрические размеры волноводной системы, составляющие от нескольких сантиметров до десятков сантиметров [3].
Общим для акустических способов создания кавитации является то, что кавитация возбуждается и развивается в одной выделенной области жидкости, называемой кавитационной областью или кавитационным облаком. Таким образом, воздействие на элемент объема газожидкостной среды осуществляется многократно, что приводит к постепенным изменениям ее свойств (газонасыщенность, размеры пузырьков, температура), причем эти изменения практически неконтролируемы. Изменение свойств среды, в свою очередь, приводит к изменению характера кавитационного воздействия. Поэтому исследование физической природы кавитационных явлений и изучение динамики пузырьков в составе кавитационного облака является достаточно сложным и неудобным.
Кавитация в потоке жидкости наблюдается в том случае, когда происходит быстрое изменение скорости потока. Изменение скорости влечет за собой, согласно уравнениям гидродинамики, изменение давления в жидкости, которое приводит к росту и последующему схлопыванию газовых пузырьков. Основным отличием от акустической кавитации является однократное воздействие на исходный микропузырек («зародыш» кавитации), поэтому резонансные методы накопления энергии газовым пузырьком в этом случае не реализуются. Существенно также, что в данном случае нет «облака» пузырьков, которые уносятся потоком жидкости, и, таким образом, нет процесса «развития» кавитации. Динамика кавитационного процесса не изменяется и однозначно определяется свойствами жидкости и характером течения. Тем не менее, изучение подобных процессов достаточно сложно, в первую очередь, из-за сложностей воспроизводимости состава и структуры кавитационных зародышей в жидкости, а также стохастических турбулентных пульсаций потока. Техническое применение в различных областях промышленности нашли кавитационные устройства в виде сужающихся трубок и гидродинамических свистков.
Высокая плотность энергии в кавитационном пузырьке объясняется, в первую очередь, очень малым объемом вещества в момент достижения пузырьком минимального радиуса. По данным разных авторов, радиус пузырька при ультразвуковой (УЗ) кавитации в конце сжатия Rmin , как правило, находится в пределах 10–10 м при равновесном (начальном) радиусе R0=(1– 10)-10-6 м. Таким образом, изменение объема пузырька (и плотности газа) составляет не менее 1000, что и вызывает экстремальную концентрацию первоначально запасенной пузырьком энергии.
Энергия запасается при расширении пузырька от равновесного радиуса R до максимального радиуса Rmax под воздействием растягивающих сил, возникающих в жидкости в фазе разрежения акустической волны. Величину запасенной энергии можно оценить как 
, где 
– изменение объёма пузырька при уменьшении его радиуса с Rmax до Rmin, P0 – давление в окружающей жидкости, которое при акустической кавитации можно принять равным статическому давлению. Если принять условие, Rmax>>Rmin, что обычно имеет место при кавитации, то для энергии получим:
. (1)
Оценки по (1) для характерных при УЗ кавитации максимальных размерах пузырька Rmax =100 мкм, и P0 = 0.1 МПа дают W=4·10-7 Дж. При сжатии такого пузырька до Rmin=0.1 мкм плотность энергии составит 10 Дж/м, что при адиабатическом нагреве идеального газа соответствует температуре более 45 000К. С учетом того, что при обычных для УЗ кавитации интенсивностях звуковых волн около I=50–100 Вт/см, что соответствует плотности акустической энергии порядка B=I/c=500 Дж/м, значение кумуляции энергии будет составлять 1015 /500=2·1012 .
Явление кумуляции энергии кавитационным пузырьком на качественном уровне легко объяснимо. Эффект заключается в том, что первоначально запасенная энергия преобразуется вначале в кинетическую энергию жидкости, сферически-симметричное движение которой по направлению к центру пузырька обуславливает бесконечное (для вакуумного пузырька) увеличение скорости сжатия, что выражается в появлении сингулярностей в решениях гидродинамических уравнений. Разумеется, физически бесконечные скорости сжатия не реализуются, чему препятствуют множество факторов, важнейшими из которых являются нарушение сферичности движения, тепломассообмен между газом и жидкостью, эндотермические химические реакции в содержимом пузырька, излучение фотонов и т.д.
Тем не менее, термодинамические параметры среды в момент коллапса пузырька достигают чрезвычайно высоких значений. По-видимому, следует считать экспериментально доказанным, что температура в пузырьке может достигать, по меньшей мере, 20 тысяч градусов [2–7].
Несмотря на то, что экспериментальное получение высокоэнергетичных кавитационных эффектов не представляет больших трудностей, а имеющийся экспериментальный материал весьма обширен, до настоящего времени не создано полностью адекватной физической модели процессов, сопровождающих пульсации кавитационного пузырька. Трудности интерпретации во многом связаны с чрезвычайно широким диапазоном изменений объема пузырька, плотности и температуры газа, а также малыми характерными интервалами времени (доли наносекунд).
Можно предположить, что в этих условиях практически невозможно описать весь комплекс происходящих процессов в рамках какой-либо одной модели. Так, например, уравнения гидродинамики становятся малопригодными для описания конечной стадии сжатия пузырька, поскольку минимальный размер пузырька близок к размерам кластеров молекул жидкости, и условие сплошности среды становятся неприменимо.
Уравнение состояния газа при плотности, превышающей плотность жидкости, и при температуре в десятки тысяч градусов также не может быть описано с точностью, достаточной для количественных оценок термодинамических параметров газа в конце сжатия. Положение еще более осложняется, если принять во внимание процессы тепломассообмена между газом и жидкостью, а также сжимаемость жидкости, которая приводит к потерям энергии пузырьком с ударными волнами.
Впервые математическое описание процесса сжатия кавитационного пузырька получил Рэлей. Он исследовал динамику пустого (вакуумного) пузырька, причем его модель учитывала только инерциальные силы и пренебрегала вязкостью, поверхностным натяжением жидкости и давлением парогазовой смеси внутри пузырька и имела вид:
. (2)
при начальных условиях:
; 
где 
– текущий радиус пузырька, а точки обозначают производные по времени t, Р0– статическое давление в жидкости, r – плотность жидкости.
Интегрируя уравнение один раз, получим закон нарастания скорости при схлопывании пузырька:
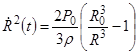. (3)
Интегрирование уравнения (3) дает времяt схлопывания пузырька:
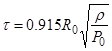. (4)
Учет давления газа в пузырьке и изменяющегося давления в жидкости, а также вязкости и поверхностного натяжения, позволяет получить более универсальное уравнение динамики кавитационного пузырька, называемое уравнением Рэлея-Плессета:
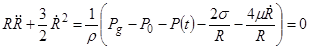, (5)
где Pg - давление газовой смеси в пузырьке, P(t) - внешнее переменное давление, m - коэффициент вязкости жидкости, s - коэффициент поверхностного натяжения жидкости.
Уравнение (5) не решается в квадратурах, однако его численное решение не представляет больших сложностей. Для этого необходимо задать вид функций Pgи P(t) и начальные условия, например, в форме (2).
Процесс сжатия обычно считается адиабатическим с показателем адиабаты g, и это находит хорошее совпадение с результатами экспериментов. В этом случае Pg вычисляется по соотношению:
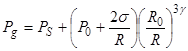. (6)
Внешнее переменное давление P(t) может быть произвольной функцией. Например, с функцией вида P(t) = Pmsin(wt) уравнение (5) описывает акустическую кавитацию с частотой колебаний давления и амплитудой звукового давления Pm. В более общем виде внешнее давление можно представить в виде: P(t)= Pmj(t), где j(t) - безразмерная функция времени.
При непериодических нагрузках, например, при ударе, фронт и спад ударного импульса описываются экспоненциальными функциями вида: 
и 
соответственно, где характерные времена tф и tс определяют скорость нарастания фронта и спада импульса давления.
На рис. 1 показаны результаты расчетов для одиночного стабильно пульсирующего пузырька (SBSL) в воде. В верхней части графика на горизонтальной линии цифрами от 1 до 10 отмечены характерные интервалы, на которых используется своя физическая модель сжатия согласно [6]. Справа вверху более детально показана динамика заключительной стадии сжатия (последние 60 нс).
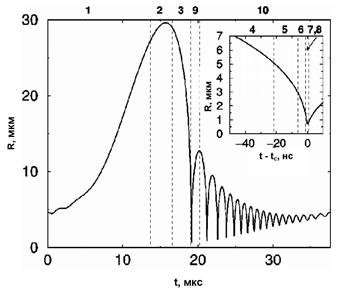
Рис. 1. Один цикл колебаний кавитационного пузырька при R0=4,5мкм, Рт=1,2бар, f=26 кГц. Вверху справа показана заключительная стадия сжатия
Согласно [6] весь цикл пульсации пузырька состоит из 10 интервалов, в течение которых протекают характерные термодинамические процессы (рис. 1). Для определенности взят пример колебаний аргонового пузырька в режиме SBSL [5, 6] при R0=4.5 мкм, f=26.5кГц и Pa=1.2 бар. При температуре жидкости 22 °С пузырек содержит приблизительно 1010 атомов аргона и приблизительно 2–10 молекул воды.
Численное интегрирование уравнений динамики пузырька дает для критического числа Рейнольдса значение Re* = 8.4. Для данной жидкости, находящейся под данным давлением, т. е. при заданных r, m и Р0, можно говорить критическом радиусе пузырька R*. При R0<R* кумуляция полностью устраняется вязкостью. Реально, критический радиус чрезвычайно мал; например, для воды R*≈0,8 мкм.
Большинство численных оценок параметров динамики кавитационных пузырьков получено с использованием уравнения Рэлея-Плессета и его модификаций. Тем не менее, следует упомянуть и более сложные модели, позволяющие учитывать сжимаемость жидкости. Одна из них описывается уравнением Херринга-Флинна [2] (7). Уравнение (7) более точно описывает динамику кавитационного пузырька с учетом сжимаемости, но только до скоростей движения, сравнимых со скоростью звука в жидкости с0:
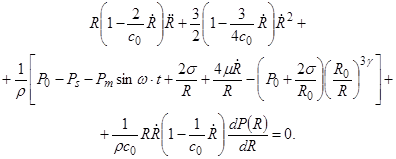. (7)
На конечной стадии захлопывания пузырька скорость стенки пузырька может превышать с0. В этом случае применяется уравнение Кирквуда-Бете [6], выведенное с допущением о сферичности волн конечной амплитуды, образующихся при схлопывании полости:
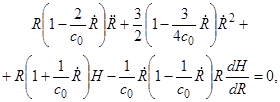. (8)
где
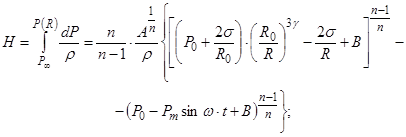
где А, В, n- постоянные коэффициенты, значения которых для воды A = 300 МПа, B= 300 МПа, n = 7.
Существует также много модификаций (например, [2]) уравнений (7) и (8). На наш взгляд, усложнение модели не способствует её точности, т.к. оно предполагает введение априорных допущений и полуэмпирических зависимостей, которые далеко не всегда с достаточной точностью описывают процессы, происходящие при коллапсе газового пузырька.
Заключение
Таким образом, в результате выполненных работ была построена математическая модель процесса схлопывания кавитационных полостей для определения выделяющейся в этом процессе энергии, позволяющих разрушить части коры и связи между корой и древесиной. Это позволит разработать комплекс рекомендаций по формированию условия работы технологического комплекса для окорки лесоматериалов ультразвуком.
Рецензенты:
Огар Пётр Михайлович, д-р техн. наук, профессор, проректор по научной деятельности ФГБОУ ВПО «Братский государственный университет», г. Братск.
Мамаев Леонид Алексеевич, д-р техн. наук, профессор, проректор по учебной работе ФГБОУ ВПО «Братский государственный университет», г. Братск.