Введение
Основу нелинейных уравнений движения блоков земной коры составляет гиперболическое уравнение синус-Гордона [5]. Для функции 
, зависящей от одной пространственной переменной x и времени t, уравнение в частных производных вида
, либо 
, (1)
носит универсальный характер в современной теории нелинейных волн [3; 5; 11; 15].
В практике геомеханических исследований геологических сред нелинейные модели применялись при исследовании сейсмичности в ротационной теории
геофизической среды автора [4], блоковой модели геофизической среды [10; 12] и при изучении кинематики подвижек по разломам авторами [1; 2; 7; 8] и многих других.
Приведение нелинейных задач геомеханики к уравнению (1) связано со свойством его полной интегрируемости [2; 3; 11], позволяющим находить решения, описывающие взаимодействие уединенных волн, называемых солитонами, в явном виде.
Автором работы [4] получено уравнение для движения блока (в виде шара) на вращающейся Земле
, (2)
которое в безразмерных координатах 
и 
приводится к уравнению (1). Если систему блоков можно представить в виде набора цилиндров (призма с ромбом в основании), то в результате действия периодической нагрузки вида 
в системе блоков возникнут возмущающие вращательные движения, в которых тела объемом V упруго сцеплены между собой. Изменение направления момента импульса одного блока приведет к появлению вокруг него упругих напряжений, которые в силу законов механики будут характеризоваться соответствующим моментом силы. Аналогично рассмотренной автором задаче [4] для данной реологии земной коры все выводы автора будут справедливы при следующих параметрах системы: радиус цилиндра 
(
); высота (глубиной залегания) 
(
); плотность 
(r = 3гсм3); момент инерции цилиндра относительно его оси 
; кинетическая энергия вращения 
, где 
- возмущение угловой скорости.
Уравнение движения (2) с учетом периодической нагрузки можно записать в виде
, (3)
где 
- вариация периодического потенциала, 
. Например, для модели упругого взаимодействия блоков 
, где 
- коэффициент трения в отсутствие периодической силы [13]. Если межблоковая среда неоднородна, то уравнение движения (2) можно представить в виде
, (4)
где 
,
- например, потенциал силы трения
, 
... b=L/2n, где L – линейный размер блока, n=1, 2, 3,…., b - линейный размер межблоковой неоднородности. В линейной теории метод малых возмущений внешних сил, обзор решений изложен в работе [6].
Рассмотрим математическую модель маятника Ньютона (рис. 1) для демонстрации блоковой модели состояния геологической среды при воздействии на неё внешней нагрузки F(m,v).
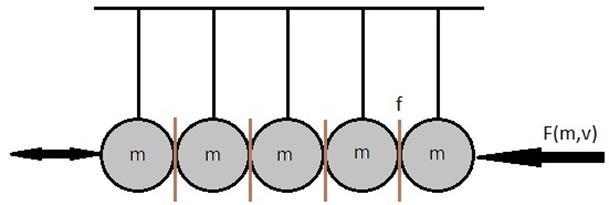
Рис. 1. Маятник Ньютона для демонстрации модели состояния среды.
Условные обозначения: m – блоки земной коры; F(m,v) – импульсная (периодическая) нагрузка; f – межблоковые шовные зоны.
Для случая консолидированного её состояния физические свойства разломов (f) и блоков (m) не различимы. Импульсное воздействие силы F(m,v) на один из блоков приведет к отрыву граничного блока (блоков) при любой длине цепочки блоков, т.е. в области с размером L=d·n, (d – диаметр блока, n – количество блоков), каждому внешнему воздействию F(m,v) можно сопоставить любое землетрясение. Вероятность таких парных событий (дуплетов) p = p(n) при достаточно большом количестве блоков (границ блоков) 
стремится к 1 
.
Для демонстрации неконсолидированного состояния массива горных пород поместим между шариками (блоками) листы бумаги (зоны f на рис. 1). В этом случае незначительное воздействие на граничный шарик (блок) приводит к полной дезинтеграции системы (разлёт блоков). Причем движение блоков в начальный период зависит от физических (упруго-вязких) свойств межблоковых зон. При увеличении длительности наблюдений вся система блоков начинает совместное движение, совершая циклические затухающие колебания. Разлет блоков в реальной геологической среде приводит к образованию динамической сейсмической бреши вследствие сильного землетрясения.
В период дезинтеграции возможно локальное деформирование отдельных частей блоковой среды и, таким образом, одна и та же система блоков может по-разному реагировать на одинаковые внешние воздействия в различные периоды наблюдений. Соотношение периодов консолидированного и неконсолидированного состояний определяется процессами в земной коре. При своем движении данный блок будет взаимодействовать только с двумя боковыми блоками, что и определит тип его движения.
Рассмотрим цепочку одинаковых из трех блоков на упругом основании и жестко связанных. Для случая радиальной силы, отклонившей блок на угол 
, действующей на i-й блок, получим уравнение движения
, (5)
где 
- сумма моментов сил, действующих в системе блоков. Например, для системы на рис. 1 для одновременно трех взаимодействующих блоков получим из (5)
, (6)
где 
- момент силы тяжести, 
- сумма моментов сил кручения со стороны соседних блоков. В обозначениях 
и 
из (3) получим уравнение 
, а в безразмерных координатах 
и 
уравнение синус-Гордона (1).
Решения уравнения (1) достаточно изучены. В приближении бегущих волн 
оно приводится к виду 
. Для 
, и, заменой переменной 
, к уравнению математического маятника [14]
. (7)
В первоначальных переменных уравнение (7) запишется в виде
или 
(8)
где 
, 
. Домножая уравнение (8) на 
и интегрируя, получим уравнение осциллятора, движущегося в потенциале 
.
. (9)
При Е=α уравнение (9) соответствуют движению по сепаратрисе. Два типа траекторий, периодические и вращательные, разделяют сепаратрисы, траектории, выходящие из особых точек 
, 
(0 и 6.28). Действительно, из (9) 
, 
. Откуда 
и после интегрирования 
, 
, или окончательно
, которое представляет собой солитонное решение в виде кинка.
В общем виде решение (1) в виде кинка, или топологического солитона, имеет вид:
, где 
= ±1 - топологический заряд кинка. Принято называть = +1 кинком, а = -1 антикинком. Параметр v - скорость кинка, причем его
значение не должно превышать предельной скорости, равной 1.
Еще одно решение уравнения синус-Гордона называется бризером или динамическим солитоном. Оно представляет собой пространственно локализованную осциллирующую нелинейную функцию, которая для случая солитона с неподвижным центром тяжести имеет вид: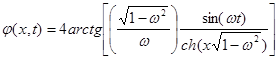 
, где 
- внутренняя частота колебаний бризера.
Взаимодействие солитонных решений не является простой суперпозицией отдельных решений. Это проявляется в том, что, при прохождении кинков друг через друга они взаимодействуют между собой, при этом изменяется фаза их движения. Решение, с учетом такого взаимодействия, можно представить в виде:
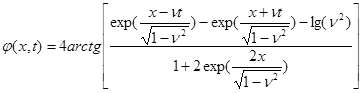
Вследствие нелинейных свойств массива горных пород происходит дополнительная деформация 
блока, 
. Напряжения на неоднородностях зависят от скорости деформирования 
, и уравнение для них может быть представлено в следующем виде [16]:
, (10)
где 
– скорость упругих поперечных волн, ρ – плотность твердого тела, 
– константа, определяющая скорость релаксации напряжений, =2·10-6 см/с (60 см/год) одинакова для всех горных пород. Решение уравнения (10) при постоянной скорости деформации 
можно представить в виде 
. Напряжение на неоднородности с течением времени меняется в пределах 
. В общем случае расчеты избыточных напряжений на неоднородностях при произвольной скорости деформирования (в том числе и с учетом нелинейности) можно рассчитать по формуле
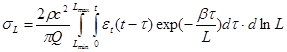, (11)
где Q – механическая добротность материала, определяемая через затухание колебаний, которая в литосфере Земли имеет порядок 102; Lmin и Lmax – размеры минимальной и максимальной неоднородностей, содержащихся в рассматриваемом объеме среды.
Таким образом, в случаях вращательного и колебательного одномерного движений однородной цепочки блоков задача сводится к анализу решений обобщенного уравнения синус-Гордона (4) при наличии малого внешнего возмущения, исследованного в работе [13].
В работе [16] сформулированы основные проблемы и направления исследований геомеханики земной коры, в которой выделены приоритетные направления исследований. В частности, выделены задачи по изучению влияния техногенных воздействий на геодинамическое состояние и устойчивость структур земной коры и инициирование техногенной сейсмичности; задачи, направленные на разработку геомеханических моделей, нацеленных на построение количественной теории деформирования земной коры и слагающих её горных массивов с учетом их неоднородного и блочно-иерархического строения.
В данной работе сделана попытка описания моделей, в которых отклик геологической среды на внешнее воздействие обусловлен состоянием межблоковых шовных зон в условиях циклических нелинейных перемещений блоков.
Рецензенты:
Максимов Евгений Петрович, доктор геолого-минералогических наук, профессор по кафедре, Технический институт (филиал) ФГАОУ ВПО «Северо-Восточный федеральный университет имени М.К. Аммосова», г. Нерюнгри.
Заровняев Борис Николаевич, доктор технических наук, профессор, декан Горного факультета Северо-Восточного федерального университета, г. Якутск.