Введение
В бумагоделательной машине широко применяются валы с полимерными покрытиями. Покрытия изготавливаются из эластомерных материалов, в частности, полиуретана и резины.
Валы прессовой части наиболее нагружены, вследствие чего покрытия имеют минимальный срок службы из-за появления дефектов, которые снижают качество вырабатываемой продукции, увеличивают вибрацию валов, поддерживающих конструкции (станин) и прессовую часть в целом [5].
Наиболее опасным дефектом, приводящим к останову машины и замене вала, является разрушение адгезионного соединения полиуретанового покрытия и рубашки вала. Различается несколько видов разрушения адгезионного соединения. Общепринятой считается следующая классификация видов разрушений: адгезионное, когезионное и смешанное. При скоростях деформирования, превышающих скорости релаксационных процессов, полимер ведет себя как твердое тело с высоким модулем упругости. В этом случае характер разрушения будет по границе раздела металл-полимер, то есть адгезионный [1]. Доля такого рода дефекта составляет порядка 90 % [6].
Разрушение может возникнуть в любом месте покрытия. Опыт эксплуатации показывает, что наиболее вероятное место разрушения – край покрытия. Такое явление принято называть краевым эффектом. Причиной любого отслоения является недостаточная адгезия покрытия с рубашкой вала. Краевой эффект возникает вследствие повышенных напряжений и больших деформаций в материале покрытия. Для снижения напряжений и деформаций покрытий по краям многие зарубежные фирмы предусматривают технологический скос.
Отсутствие уточненных методов расчета краевого эффекта не позволяет многим отечественным производителям принимать обоснованную геометрию скоса покрытия, поэтому приходиться заимствовать форму скоса у иностранных компаний, что не всегда приводит к нужным результатам. Угол и длина скоса не постоянны и зависят от физико-механических характеристик материала, от толщины покрытия и других условий.
Для разработки методов расчета покрытий с учетом краевого эффекта в зависимости от условий нагружения, физико-механических свойств покрытия, наиболее актуальными представляются исследования напряженно-деформированного состояния (НДС) покрытий. Данная методика позволит обоснованно выбирать геометрические параметры скосов по краям покрытий и устанавливать причины разрушений покрытий из полиуретана в условиях эксплуатации валов.
При разработке методов расчета покрытий с учетом краевого эффекта проводим анализ параметров НДС в зоне контакта по краям валов, путем постановки следующих задач:
определения зависимости твердости и геометрии скоса покрытия при нагружении;
определения величины деформаций, максимального напряжения сдвига, нормальных напряжений на краях покрытия при различной геометрии скоса.
На основании проведенных исследований сформулировать рекомендации по рациональной геометрии скоса.
Моделирование контакта двух цилиндров с покрытием реализуем в конечно–элементном пакете Ansys (в рамках обучающих лицензий и студенческих версий программ).
Вследствие симметрии модели для сокращения времени расчета и повышения точности результатов целесообразно использовать ¼ часть геометрической модели (рис. 1).
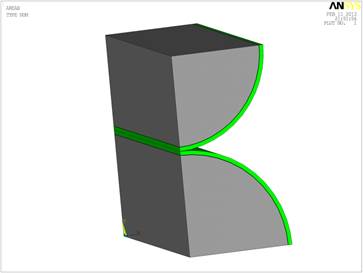
Рис. 1. Геометрическая модель контакта валов
Задача контакта двух цилиндров, имеющих эластомерные покрытия, относится к классу контактных задач flexible-to-flexible, когда жесткости контактируемых тел близки и происходит деформирование обоих тел [3]. В предположительной зоне контакта валов моделируется симметричный контакт (так как свойства контактирующих тел подобны) без трения, с использованием 3D конечных элементов (КЭ) CONTA 174 и TARGE 170 (для контакта типа surface - to - surface). На валы наносятся элементы PLANE 82, на покрытия наносятся элементы SOLID 185 с назначением соответствующего материала. Покрытие крепится к рубашке вала с помощью связующего слоя, элементами типа LINK11. Оба вала имеют соответствующие закрепления: нижний вал зафиксирован во всех трех направлениях. Верхнему валу назначена одна степень свободы вдоль вертикальной оси ОY и приложена нагрузка в виде давления, которое создает линейное давление в зоне контакта 100 кН/м. Конечно-элементная модель валов представлена на рис. 2.
В качестве исследуемых покрытий были приняты полиуретаны с твердостью 95 ШорА и 70 ШорD. Данные материалы широко используются для покрытий валов бумагоделательных машин. Для моделирования гиперупругих материалов, к которым относятся полиуретаны, необходимо выбрать модель поведения материала на основе данных диаграммы «напряжение-деформация», полученной на разрывной машине.
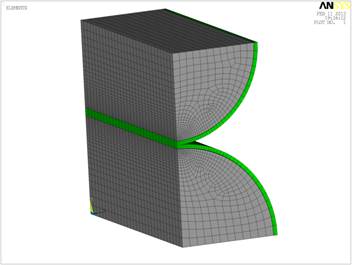
Рис. 2. Конечно-объемная модель контакта валов
Диаграммы «напряжение-деформация» для используемых материалов показаны на рис. 3.
а 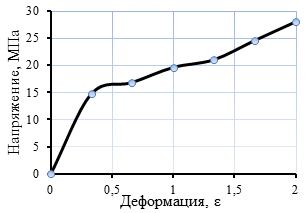 б
б 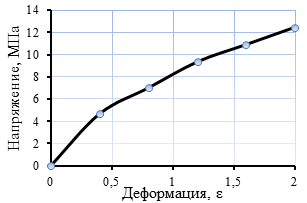
Рис. 3. Диаграмма «напряжение-деформация»: а – полиуретан твердостью 70 ШорD, б – полиуретан твердостью 95 ШорА
Данные модели поведения материалов хорошо аппроксимируются моделью Муни-Ривлина с тремя параметрами (рис. 4).
Плотность энергии деформации для материала Муни-Ривлина с тремя параметрами имеет вид [7]:
![]() (1)
(1)
где С10, С01, С11 – константы материала, характеризующие девиатор деформации материала, ![]() ,
, ![]() – первая и вторая инварианты девиатора деформаций,
– первая и вторая инварианты девиатора деформаций, ![]() ,
, ![]() – параметр сжимаемости материала, J – относительное изменение объема.
– параметр сжимаемости материала, J – относительное изменение объема.
Константы материала с твердостью 70 шорD: С10 = -8,64·106 Па, С01 = 2,33·107 Па, С11 = 1,08·106 Па.
Константы материала с твердостью 95 шорА: С10 = 1,64·106 Па, С01 = 1,34·106 Па, С11 = 1,59·104 Па.
а 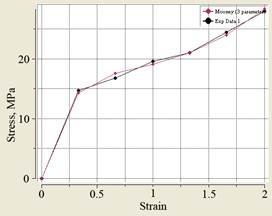 б
б 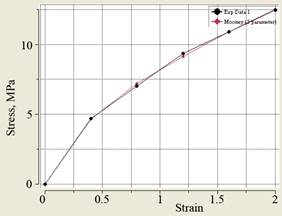
Рис. 4. Аппроксимация поведения материала моделью Муни-Ривлина с тремя
параметрами: а – полиуретан твердостью 70 ШорD, б – полиуретан твердостью 95 ШорА
Геометрия скосов, используемых в исследовании, приведена на рис. 5, а геометрические размеры в таблице 1.
а 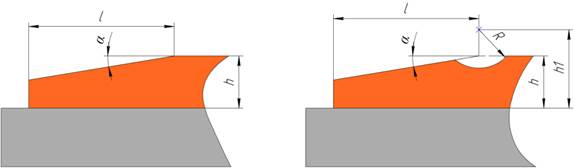 б
б
Рис. 5. Геометрии скоса покрытия: а – скос № 1, б – скос № 2
Таблица 1
|
Размер |
Скос №1 |
Скос №2 |
|
Толщина покрытия h, мм |
20 |
20 |
|
Угол наклона α, град |
5 |
20 |
|
Длина скоса l, мм |
20 |
20 |
|
Радиус R, мм |
– |
10 |
|
Расстояние до центра окружности h1, мм |
– |
20 |
Для расчета напряжений и деформаций используем основные соотношения теории упругости в матричном виде [2].
Связь перемещения {q} в узлах конечно-элементной модели с деформацией определяется выражением:
{ε} = [B]{q}, (2)
где {ε} – деформации узлов конечных элементов; [B] – матрица перехода от перемещений узлов к деформациям в произвольной точке [4].
Напряжения определяются по формуле:
{σ} = [D]{ε}, (3)
где {σ} – напряжения узлов конечных элементов; [D] – матрица модуля упругости материала.
Результаты расчетов напряжений и деформации сведены в таблицу 2, картины напряжений и деформаций для материала с твердостью 70 ШорD показаны на рисунке 6, для материала с твердостью 95 ШорА рисунке 7.
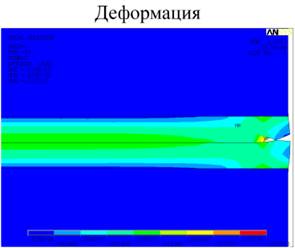

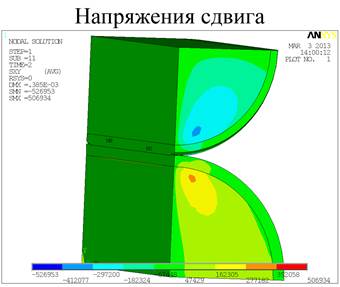
Рис. 6. Результаты численных расчетов
Таблица 2
|
Параметры |
Твердость покрытия |
Скос № 1 |
Скос № 2 |
Без скоса |
|
Линейное давление 100 кН/м |
||||
|
Макс. нормальные напряжения, МПа |
70D |
4,6 |
2,4 |
4,9 |
|
Макс. напряжения сдвига, МПа |
0,57 |
0,27 |
0,63 |
|
|
Макс. деформации в покрытии |
0,027 |
0,022 |
0,029 |
|
|
Макс. нормальные напряжения, МПа |
95A |
4,7 |
2,02 |
5,03 |
|
Макс. напряжения сдвига, МПа |
0,57 |
0,43 |
0,62 |
|
|
Макс. деформации в покрытии |
0,132 |
0,103 |
0,138 |
|


Рис. 7. Результаты численных расчетов
В статье приведены количественные и качественные результаты моделирования напряженно-деформированного состояния покрытий валов по краям. Было установлено, что увеличение угла скоса приводит к снижению напряжений и деформаций по краям покрытий. Форма скоса также влияет на величину действующих напряжений и деформаций в покрытии. Расчет показал, что значения напряжений в покрытии для скоса № 2 в два раза меньше, чем в покрытии без технологического скоса. Величина деформации снижается на 25 %. Величина напряжений и деформаций в покрытии для скоса № 1 незначительно меньше, чем в покрытии без скоса. Это показывает, что данная геометрия неудачна и не дает желаемого результата. Таким образом, правильно подобранная геометрия скоса дает существенное снижение напряжений и деформаций по краям покрытий, что повышает долговечность покрытия.
Результаты расчетов показали необходимость индивидуального выбора формы скоса для каждого конкретного вала, с учетом физико-механических свойств материала покрытия и величины линейного давления между валами.
Данная методика может помочь при выборе геометрии скоса на полимерных покрытиях валов и может быть рекомендована производителям полимерных покрытий.
В дальнейшем планируются расширить исследования напряженно-деформированного состояния покрытий по краям путем увеличения номенклатуры геометрических форм скосов.
Рецензенты:
Сиваков Валерий Павлович, доктор технических наук, профессор кафедры машин и оборудования ЦБП, УГЛТУ, г. Екатеринбург.
Кащенко Михаил Петрович, доктор физико-математических наук, профессор кафедры физики, УГЛТУ, г. Екатеринбург.



