Среди проблем инновационной модернизации современного высшего заочного образования [8–10] особенно активно обсуждается внедрение современных информационных образовательных интернет-технологий в организацию заочного обучения, совершенствование содержания учебного процесса и контроля знаний [4–5]. Сегодня самым современным и перспективным средством технологической поддержки дистанционного обучения являются сетевые интернет-технологии в форме сервера дистанционного обучения, обеспечивающего интерактивную среду управления процессом познавательной деятельности, связь с учащимися через интернет, в том числе в режиме реального времени, и доступ к современным информационно-коммуникационным ресурсам. Такие сетевые интернет-технологии вытесняют в последнее время другие формы технологий, в частности, традиционную классическую кейс-технологию.
В Томском политехническом университете (ТПУ) [6] начиная с 2008 г. в учебном процессе применяются элементы телекоммуникационной и сетевой технологий (on-line трансляция лекций в режиме live-video, вебинары, on-line тестирования студентов, образовательные форумы). Использование информационно-коммуникационных технологий способствовало введению в современный процесс обучения для части студентов-заочников первого курса новой формы обучения, использующей современные дистанционные образовательные технологии (ДОТ) на платформе обучающей электронной среды Moodle, позволяющей студенту активно взаимодействовать с преподавателем через интернет. При этом для обучения большей части студентов-заочников продолжала применяться классическая форма обучения с использованием кейс-технологии (КТ), предполагавшей преимущественно самостоятельную работу студента с комплексом учебно-методических материалов по дисциплине. Таким образом, в переходный период в Институте дистанционного образования ТПУ были реализованы две модели организации заочного обучения по техническим направлениям: КТ, в рамках которой экзаменационные сессии проходили традиционно в Томске, и ДОТ, в рамках которой сессии проходили через интернет посредством on-line тестирования. Студенты технических направлений, обучавшиеся первые два курса в рамках модели ДОТ, начиная с 3-го курса, были переведены на КТ модель организации заочного обучения. Данное обстоятельство позволило провести сравнительный статистический анализ (аналогично [1–3, 7]) качества успеваемости студентов разных заочных форм обучения (ЗФО). В статистическом анализе использованы экзаменационные результаты (в 100-балльной шкале, приведенной к 5-балльной шкале) по высшей математике II, III и V семестров (ЭКЗII, ЭКЗIII и ЭКЗV) студентов-заочников Энергетического института ТПУ. Отдельной выборкой оформлены экзаменационные результаты студентов, академически восстановленных (АВ) до V-го семестра. Для сравнения динамики экзаменационных результатов (ЭКЗII, ЭКЗIII и ЭКЗV) в зависимости от ЗФО (КТ, ДОТ и АВ) введен 3-х уровневый фактор ЭКЗ (ЭКЗII, ЭКЗIII и ЭКЗV) повторных измерений и применен однофакторный (3-х уровневый фактор ЗФО) дисперсионный анализ с 3-х уровневым фактором ЭКЗ повторных измерений.
Заметим, что, согласно теории измерительных шкал, балльная шкала относится к типу порядковых шкал, позволяющих ранжировать (упорядочить) результаты оценивания качества усвоения знаний студентов. Поэтому в балльной шкале оперирование средним баллом является некорректным, а обоснованным является использование медиан вместо средних баллов. В связи с этим для сравнения рассматриваемых выборок предлагается использовать ранговые (непараметрические) критерии, основанные на рангах, а не на средних значениях.
Для каждой выборки взаимодействия факторов ЗФО*ЭКЗ кроме объема n рассчитаны числовые непараметрические характеристики: медиана Ме, минимум Мин, максимум Макс, нижняя квартиль (25 % процентиль) и верхняя квартиль (75% процентиль), приведенные в табл. 1.
Таблица 1. Числовые характеристики выборок ЗФО*ЭКЗ
|
ЗФО |
ЭКЗ |
n |
Ме |
Мин |
Макс |
25% |
75% |
|
АВ |
ЭКЗII |
15 |
2,75 |
2,75 |
4,50 |
2,75 |
3,50 |
|
АВ |
ЭКЗIII |
15 |
2,75 |
2,75 |
4,50 |
2,75 |
3,50 |
|
АВ |
ЭКЗV |
15 |
2,75 |
1,25 |
3,50 |
2,75 |
3,00 |
|
ДОТ |
ЭКЗII |
46 |
3,00 |
2,60 |
4,50 |
2,85 |
3,50 |
|
ДОТ |
ЭКЗIII |
46 |
3,50 |
2,70 |
4,50 |
2,75 |
3,80 |
|
ДОТ |
ЭКЗV |
46 |
2,75 |
1,50 |
3,25 |
2,75 |
2,95 |
|
КТ |
ЭКЗII |
90 |
2,75 |
2,75 |
4,50 |
2,75 |
3,50 |
|
КТ |
ЭКЗIII |
90 |
2,75 |
1,25 |
4,50 |
2,75 |
3,50 |
|
КТ |
ЭКЗV |
90 |
2,75 |
0,50 |
4,00 |
2,75 |
3,00 |
Применение непараметрического (рангового) дисперсионного анализа Фридмана с повторными измерениями позволило оценить различия между результатами ЭКЗII, ЭКЗIII и ЭКЗV по их совокупности, то есть динамику экзаменационных результатов, для ДОТ (взаимодействие ДОТ*ЭКЗ) как высоко значимые (на уровне значимости р < 0,00005) , а для КТ (КТ*ЭКЗ) или АВ (АВ*ЭКЗ) как незначимые (на уровне значимости р > 0,10). Заметим для сравнения, что в случае КТ результаты ЭКЗV и ЭКЗIII различаются согласно парному непараметрическому критерию Вилкоксона слабо незначимо (на уровне значимости р ≈ 0,12 > 0,10). При этом согласно парным непараметрическим критериям знаков и Вилкоксона для зависимых выборок в случае ДОТ результаты ЭКЗV отличаются как от ЭКЗII, так и от ЭКЗIII высоко значимо (на уровне значимости р < 0,00005), а ЭКЗII и ЭКЗIII различаются статистически значимо (на уровне 0,001 < р < 0,05). Последнее различие (нестабильность ЭКЗII и ЭКЗIII в случае ДОТ) можно объяснить, по-видимому, в значительной степени несовершенством технического обеспечения процесса проведения и оформления результатов новой формы обучения ДОТ на начальном этапе ее внедрения в учебный процесс. С другой стороны, в рамках однофакторного дисперсионного анализа независимых выборок с помощью непараметрического критерия Краскела-Уоллиса можно оценить различия между экзаменационными результаты разных ЗФО (КТ, ДОТ и АВ) как незначимые (р > 0,10) в случае ЭКЗV (ЗФО*ЭКЗV), как статистически значимые (на уровне 0,001 < р < 0,05) в случае ЭКЗII (ЗФО*ЭКЗII) за счет различий между КТ*ЭКЗII (или АВ*ЭКЗII) и ДОТ*ЭКЗII и, наконец, как сильно значимые (на уровне 0,00005 < р < 0,001) в случае ЭКЗIII (ЗФО*ЭКЗIII) за счет различий между КТ*ЭКЗIII (или АВ*ЭКЗIII) и ДОТ*ЭКЗIII. Графические числовые непараметрические характеристики (диаграммы размаха) выборок экзаменационных результатов разных ЗФО представлены на рис. 1.
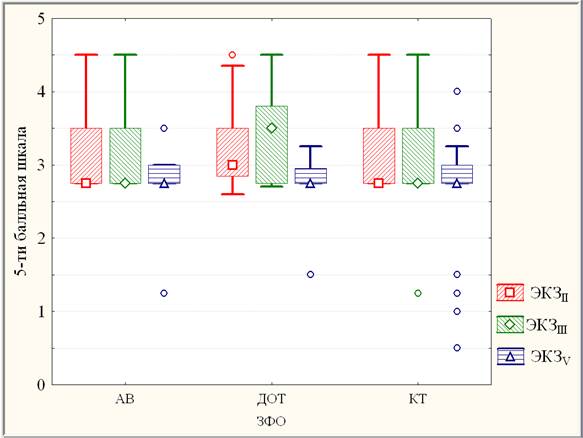
Рис. 1. Медианные диаграммы размаха выборок экзаменационных результатов ЗФО*ЭКЗ
Обозначения: метки «квадрат», «ромб», «треугольник» - медианы; метка «круг» – выбросы; ящик – квартильный размах (25 % – 75 %); отрезки – размах без выбросов
Полученные результаты оценки значимости различий разных выборок взаимодействия факторов ЗФО*ЭКЗ, а также дополнительные обстоятельства однородности отдельных выборок взаимодействия факторов ЗФО*ЭКЗ, позволяют сократить их количество.
С одной стороны, не значимость (на основании непараметрического дисперсионного анализа Фридмана с повторными измерениями) различия динамик экзаменационных результатов (ЭКЗII, ЭКЗIII и ЭКЗV) для КТ и АВ, а также близость выборки АВ по форме обучения к КТ, допускает возможность объединить две выборки АВ и КТ в одну выборку АВ+КТ.
С другой стороны, учитывая однородность экзаменационных результатов ЗФО*ЭКЗII и ЗФО*ЭКЗIII в смысле форм обучения, а также выше полученные результаты оценки значимости различий ЭКЗII и ЭКЗIII для разных ЗФО (ДОТ и КТ), можно вместо двух выборок ЗФО*ЭКЗII и ЗФО*ЭКЗIII рассмотреть одну выборку ЗФО*ЭКЗII+III, построенную усреднением экзаменационных результатов ЗФО*ЭКЗII и ЗФО*ЭКЗIII .
Таким образом, речь идет о сравнении выборок взаимодействия 2-х уровневого фактора экзаменационных результатов ЭКЗ2 (ЭКЗII+III и ЭКЗV) повторных измерений с 2-х уровневым фактором ЗФО2 форм обучения (ДОТ и АВ+КТ), то есть об оценивании различия динамики экзаменационных результатов (сравнение ЭКЗII+III с ЭКЗV) для разных форм обучения (ДОТ и АВ+КТ). Диаграммы размаха выборок экзаменационных результатов ЭКЗ2 разных форм обучения ЗФО2 представлены на рис. 2.
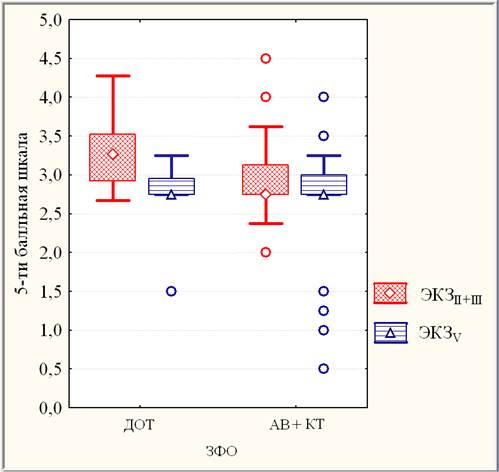
Рис. 2. Медианные диаграммы размаха выборок экзаменационных результатов ЗФО2*ЭКЗ2
Обозначения: метки «ромб», «треугольник» – медианы; метка «круг» – выбросы; ящик – квартильный размах (25 % – 75 %); отрезки – размах без выбросов
На основании дисперсионного анализа Фридмана различия между результатами ЭКЗII+III и ЭКЗV оценены как высоко значимые (р < 0,00005) в случае ДОТ и как незначимые (р ≈0,25 > 0,10) для АВ+КТ. С другой стороны, на основании критерия Краскела-Уоллиса различия между экзаменационными результатами разных форм обучения ДОТ и АВ+КТ оценены как незначимые (р > 0,10) в случае ЭКЗV и как сильно значимые (0,00005 < р ≈ 0,0005 < 0,001) в случае ЭКЗII+III .
Таким образом, на основании непараметрического дисперсионного анализа экзаменационных результатов трех семестров по высшей математике в зависимости от формы заочного обучения сделаны следующие выводы: сильно значимое различие (0,00005< р < 0,001) между ДОТ и КТ в экзаменационных результатах, усредненных по 2-му и 3-му семестрам, в результате дальнейшей отрицательной динамики (сравнение экзаменационных результатов, усредненных по 2-му и 3-му семестрам, с 5-ым), высоко значимой для ДОТ и не значимой для КТ, привело к незначимому (р > 0,10) различию между ДОТ и КТ в 5-ом семестре.
В связи с аномально высокими экзаменационными результатами ДОТ в 3-ем семестре можно заметить, что стадия оценивания усвоенных студентом знаний при дистанционном обучении с использованием информационных образовательных интернет-технологий может иметь специфический нюанс идентификации студента: преподаватель должен быть уверен, что на другом конце телекоммуникационной цепочки находится именно тот человек, который претендует на получение не только определенных знаний, но и документа (диплома, свидетельства, удостоверения, сертификата) об освоении соответствующей образовательной программы [4]. При дистанционном обучении стадия оценивания качества учебных достижений студентов («Контроль и оценка») в определенном смысле является центральной. Здесь очень важен вопрос о защите данных и средствах идентификации студента, не допускающих подмену и искажение результатов тестирования. В случае дистанционного обучения эти трудности могут быть преодолены за счет проведения контрольных испытаний студента в специально оборудованных учебных помещениях либо в присутствии лиц, находящихся в полном доверии у преподавателя и администрации учебного центра [4], либо в режиме видеотелефонной связи через интернет посредством Skype. Альтернативой может быть проведение экзаменационного контроля заключительного этапа дистанционного изучения дисциплины в классической форме, позволяющей преподавателю-экзаменатору оценить достигнутый студентом уровень усвоения материала посредством экзамена в письменной форме под контролем преподавателя с обязательным собеседованием.
Одной из значимых составляющих ДОТ является система тестирования в среде дистанционного обучения Moodle [5]. Она должна обеспечивать текущий контроль знаний, а на завершающей стадии дать объективную оценку знаний студента, на основании которой происходит выдача сертификатов, дипломов и пр. К сожалению, качество формы самих контрольно-измерительных тестовых материалов, технического обеспечения процесса проведения и оформления результатов тестирования оставляет желать лучшего, требует постоянного совершенствования, что ограничивает применение системы тестирования рамками текущего контроля знаний и, в лучшем случае, базового итогового контроля знаний (на уровне «зачтено – не зачтено»).
Немаловажным обстоятельством на стадии «Контроль и оценка» является оптимизация рейтинговой системы оценивания разных составляющих (вебинары, рубежный тестовый контроль, индивидуальные домашние задания) процесса дистанционного обучения.
В целом же, совершенствование ДОТ должно быть направлено на приближение дистанционное образование к апробированному столетиями традиционному очному, на использование Интернета и других систем передачи данных для обеспечения возможности непосредственного общения преподавателя со студентом, на совершенствование системы управления самостоятельной деятельностью студентов-заочников в семестре и модернизации методики проведения итогового контроля.
Реализация инновационных ДОТ должна решить ряд существенных проблем, связанных с разработкой, а также техническим и программным сопровождением принципиально новой методики преподавания, учитывающей особенности данного вида коммуникации и обеспечивающей проведение всех форм занятий для удаленной аудитории. К таким проблемам относятся, прежде всего, организация в режиме реального времени (on-line) видеоконференцсвязи при чтении лекций с возможностью текущего опроса, проведение интерактивных занятий в компьютерном классе удаленной аудитории, позволяющее в режиме реального времени управлять работой студентов на компьютерах, проведение различных форм контроля (в том числе и итогового) в режиме реального времени.
Результаты проведенного статистического анализа классической и сетевой дистанционной моделей организации заочного обучения могут быть учтены в рамках проходящей реформы высшего образования.
Выводы
1. В рамках дисперсионного анализа экзаменационных результатов студентов-заочников, обучавшихся по классической КТ и дистанционной сетевой ДОТ формам, выявлено сильно значимое различие (0,00005< р < 0,001) между ДОТ и КТ в экзаменационных результатах, усредненных по 2-му и 3-му семестрам, которое в ходе дальнейшей отрицательной динамики (сравнение экзаменационных результатов, усредненных по 2-му и 3-му семестрам, с 5-ым), высоко значимой для ДОТ и не значимой для КТ, привело к незначимому (на уровне значимости р > 0,10) различию между ДОТ и КТ в 5-ом семестре.
2. Предложены способы устранения значимых различий между ДОТ и КТ в рамках проходящей реформы высшего образования.
Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.
Рецензенты:
Трифонов Андрей Юрьевич, д-р физ.-мат. наук, профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев Константин Петрович, д-р физ.-мат. наук, профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.



