Введение
Подавляющее большинство задач прикладной статистики сводится к необходимости оценки дисперсионно-ковариационной матрицы (ДКМ) наблюдения вектора случайных величин ![]() , распределенных по многомерному нормальному закону. Из [1; 7] и многих других источников известно, что существующие аналитические методы определения элементов ДКМ на практике сводятся к оценке [1]:
, распределенных по многомерному нормальному закону. Из [1; 7] и многих других источников известно, что существующие аналитические методы определения элементов ДКМ на практике сводятся к оценке [1]:
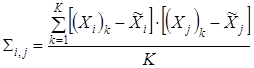 ;
; ![]() , (1)
, (1)
где K – объем выборки элементов вектора случайных величин ![]() ;
; ![]() и
и ![]() – выборочные средние i-го и j-го элементов вектора случайных величин
– выборочные средние i-го и j-го элементов вектора случайных величин ![]() , значение которых определяются известным отношением [7]:
, значение которых определяются известным отношением [7]:
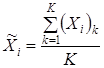 . (2)
. (2)
Однако правило (1) не определяет максимально правдоподобную оценку ДКМ ![]() . Другие решения, к примеру [3–5] и др., нахождения ДКМ по известной статистике (конечному набору наблюдений элементов вектора
. Другие решения, к примеру [3–5] и др., нахождения ДКМ по известной статистике (конечному набору наблюдений элементов вектора ![]() ) направлены на численное решение градиентными релаксационными методами условных оптимизационных задач по критерию максимума правдоподобия, что в свою очередь не позволяет достигнуть точного определения оптимума целевой функции правдоподобия и в виду итеративного подхода значительно увеличивает вычислительную сложность процесса оценки.
) направлены на численное решение градиентными релаксационными методами условных оптимизационных задач по критерию максимума правдоподобия, что в свою очередь не позволяет достигнуть точного определения оптимума целевой функции правдоподобия и в виду итеративного подхода значительно увеличивает вычислительную сложность процесса оценки.
Цель статьи заключается в получении аналитического выражения максимально правдоподобной оценки ДКМ для произвольного размера вектора случайных величин ![]()
![]() , распределенных по многомерному нормальному закону.
, распределенных по многомерному нормальному закону.
Теорема о максимально правдоподобной оценке ДКМ
Теорема. Пусть ![]() есть конечная последовательность векторов размерности N случайных величин, определенных в области действительных чисел R, и распределенных по многомерному нормальному закону. Тогда максимально правдоподобная оценка ДКМ
есть конечная последовательность векторов размерности N случайных величин, определенных в области действительных чисел R, и распределенных по многомерному нормальному закону. Тогда максимально правдоподобная оценка ДКМ ![]() полученной выборки объема K определяется отношением:
полученной выборки объема K определяется отношением:
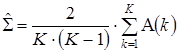 , (3)
, (3)
где ![]() – наблюдаемая ДКМ на выборке вектора случайных величин размера k, определяемая отношением:
– наблюдаемая ДКМ на выборке вектора случайных величин размера k, определяемая отношением:
![]() . (4)
. (4)
Доказательство. Поскольку элементы вектора ![]() определены в области действительных чисел R и распределены по многомерному нормальному закону, то функция плотности распределения наблюдаемой ДКМ
определены в области действительных чисел R и распределены по многомерному нормальному закону, то функция плотности распределения наблюдаемой ДКМ ![]() , формируемой конечной последовательности наблюдаемых векторов
, формируемой конечной последовательности наблюдаемых векторов ![]() , согласно [8] определяется выражением (функция распределения плотности вероятности Уишарта):
, согласно [8] определяется выражением (функция распределения плотности вероятности Уишарта):
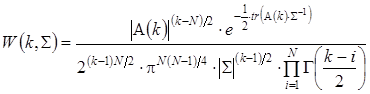 , (5)
, (5)
где ![]() – оператор, определяющий величину следа матрицы;
– оператор, определяющий величину следа матрицы;![]() – наблюдаемая на выборке размера k ДКМ и определяемая известным отношением [1]:
– наблюдаемая на выборке размера k ДКМ и определяемая известным отношением [1]:
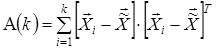 . (6)
. (6)
В выражении (6) ![]() – вектор выборочных средних элементов вектора случайных величин
– вектор выборочных средних элементов вектора случайных величин ![]() .
.
Согласно представленному равенству (5) составим функцию максимально правдоподобной оценки ДКМ ![]() по известным конечным наблюдениям векторов случайных величин
по известным конечным наблюдениям векторов случайных величин ![]() :
:
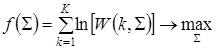 . (7)
. (7)
Для нахождения точек экстремума определим аналитический дифференциал скалярной функции (7) от матриц по матричному аргументу, в соответствии с правилами, представленными в [2]:
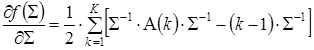 . (8)
. (8)
Приравняв полученную систему уравнений к нулю, определим корни, удовлетворяющие условию:
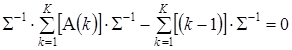 . (9)
. (9)
Заметим, что 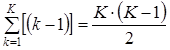 , тогда получим равенство (9) в виде:
, тогда получим равенство (9) в виде:
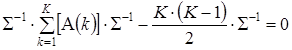 . (10)
. (10)
Помножив обе части равенства (10) на ![]() , получим:
, получим:
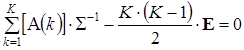 , (11)
, (11)
где ![]() – единичная матрица размерности
– единичная матрица размерности ![]() .
.
Выразив ![]() в выражении (11), получим:
в выражении (11), получим:
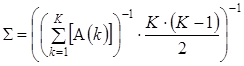 . (12)
. (12)
Раскрыв в правой части равенства (12) скобки, получим:
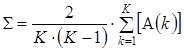 . (13)
. (13)
Заметим, что для уменьшения вычислительной сложности определения ДКМ выражением (13) наблюдаемую матрицу ![]() на выборки объемом k, рассчитываемую в соответствии с выражением (6), можно справедливо представить в виде:
на выборки объемом k, рассчитываемую в соответствии с выражением (6), можно справедливо представить в виде:
![]() . (14)
. (14)
Очевидно, что ввиду линейности системы уравнений (9) решение (13) является для целевой функции (7) единственной точкой экстремума, а из унимодальности функции (5) следует, что найденной решение (13) соответствует точке, удовлетворяющей правилу (7), и максимально правдоподобная оценка ДКМ справедливо запишется в виде (3). Теорема доказана.
Аналогичным образом определяется максимально правдоподобная оценка ДКМ ![]() , формируемой
, формируемой ![]() конечной последовательностью векторов размерности N случайных величин, определенных в области комплексных чисел С и распределенных по многомерному нормальному закону. В данном случае ДКМ будет рассчитываться выражением:
конечной последовательностью векторов размерности N случайных величин, определенных в области комплексных чисел С и распределенных по многомерному нормальному закону. В данном случае ДКМ будет рассчитываться выражением:
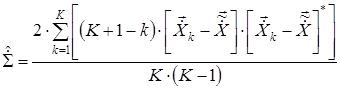 , (15)
, (15)
где ![]() – оператор комплексного сопряжения.
– оператор комплексного сопряжения.
Оценка полученных результатов
Для определения качества оценки по полученному выражению (3) оценки ДКМ определим зависимость нижней границы дисперсии оценки ![]() от объема выборки K и размерности N вектора наблюдений
от объема выборки K и размерности N вектора наблюдений ![]() из многомерного неравенства Крамера-Рао [7]:
из многомерного неравенства Крамера-Рао [7]:
![]() , (16)
, (16)
где ![]() – след обратной информационной матрицы Фишера, определяемой соотношением [7]:
– след обратной информационной матрицы Фишера, определяемой соотношением [7]:
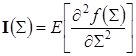 , (17)
, (17)
где ![]() – оператор математического ожидания.
– оператор математического ожидания.
Для определения элементов информационной матрицы Фишера ![]() представим её в виде блочной матрицы:
представим её в виде блочной матрицы:
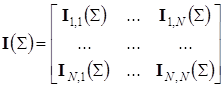 . (18)
. (18)
Затем, воспользовавшись правилами дифференцирования матричной функции по матричному аргументу, сформированными в [6], определим i-е, j-е элементы (подматрицы) блочной матрицы (17):
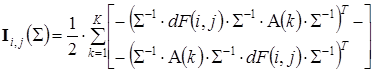 , (19)
, (19)
где ![]() – матричная функция размерности
– матричная функция размерности ![]() , n-е, m-е
, n-е, m-е ![]() элементы которой определяются согласно выражению:
элементы которой определяются согласно выражению:
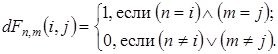 (20)
(20)
На рисунках 1–4 представлена зависимость дисперсии оценки ![]() ДКМ, произведенной по известному выражению (1) и полученному – (3), от объема выборки K для вектора наблюдений
ДКМ, произведенной по известному выражению (1) и полученному – (3), от объема выборки K для вектора наблюдений ![]() , распределенного по многомерному нормальному закону, размерности 2, 4, 6, 8 соответственно.
, распределенного по многомерному нормальному закону, размерности 2, 4, 6, 8 соответственно.
а) 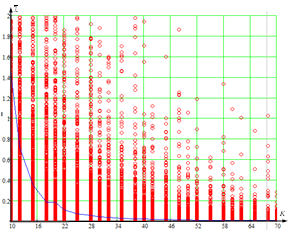 б)
б)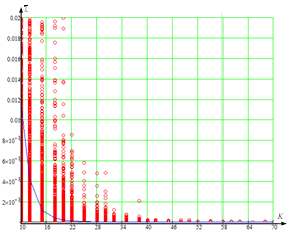
Рисунок 1 – Зависимость дисперсии оценки ![]() от объема выборки K для размера вектора наблюдений, равного 2 (N = 2)
от объема выборки K для размера вектора наблюдений, равного 2 (N = 2)
(а – оценка ДКМ выражением (1); б – оценка ДКМ выражением (3)).
а)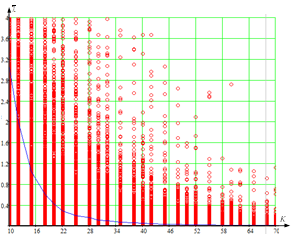 б)
б)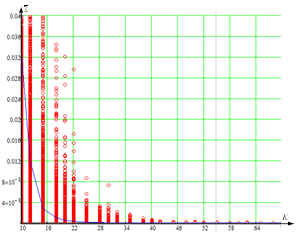
Рисунок 2 – Зависимость дисперсии оценки ![]() от объема выборки K для размера вектора наблюдений, равного 4 (N = 4)
от объема выборки K для размера вектора наблюдений, равного 4 (N = 4)
(а – оценка ДКМ выражением (1); б – оценка ДКМ выражением (3)).
а)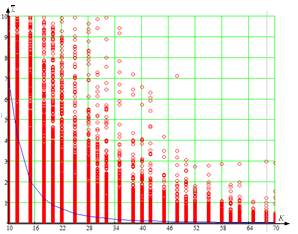 б)
б)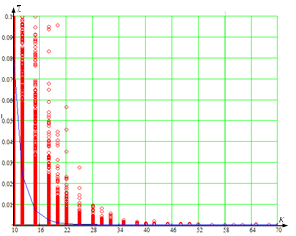
Рисунок 3 – Зависимость дисперсии оценки ![]() от объема выборки K для размера вектора наблюдений, равного 6 (N = 6)
от объема выборки K для размера вектора наблюдений, равного 6 (N = 6)
(а – оценка ДКМ выражением (1); б – оценка ДКМ выражением (3)).
а)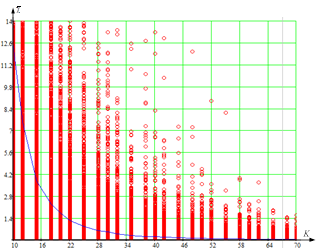 б)
б)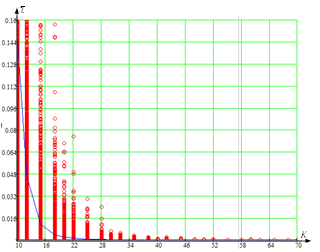
Рисунок 4 – Зависимость дисперсии оценки ![]() от объема выборки K для размера вектора наблюдений, равного 8 (N = 8)
от объема выборки K для размера вектора наблюдений, равного 8 (N = 8)
(а – оценка ДКМ выражением (1); б – оценка ДКМ выражением (3)).
На рисунке 5 представлены графики зависимости отношения дисперсии оценки ДКМ выражением (3) к дисперсии оценки ДКМ выражением (1) от объема выборки K, для N равном 2, 4, 6.
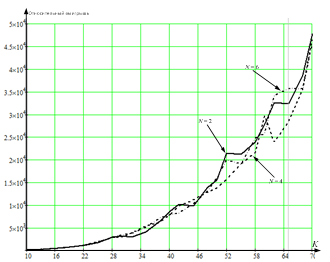
Рисунок 5 – Зависимость отношения дисперсии оценки ДКМ выражением (3) к дисперсии оценки ДКМ выражением (1) от объема выборки K, для N = 2, 4, 6.
Выводы
Из полученных результатов следует, что наряду с очевидным улучшением точности оценки ДКМ выражениями (1) и (3) с ростом объема выборки вектора случайных величин предложенное выражение (3) максимально правдоподобной оценки ДКМ приводит к существенному увеличению точности оценки ДКМ (на величину порядка нескольких тысяч раз) уже на выборках малого объема независимо от разрядности ДКМ (размера вектора случайных величин). Такая ситуация обуславливает очевидную предпочтительность оценки ДКМ вектора случайных величин![]() произвольной размерности
произвольной размерности ![]() , распределенных по многомерному нормальному закону, полученным аналитическим выражением (3) по сравнению с известным и применяемым на практике отношением (1).
, распределенных по многомерному нормальному закону, полученным аналитическим выражением (3) по сравнению с известным и применяемым на практике отношением (1).
Рецензенты:
Архипов Н.С., доктор технических наук, доцент, сотрудник Академии ФСО России, г. Орел.
Сычев К.И., доктор технических наук, доцент, сотрудник Академии ФСО России, г. Орел.



