Динамические процессы в механических устройствах с контактирующими и трущимися элементами в кинематических парах, таких как направляющие суппортов станков, робототехнические системы, фрикционные муфты, сцепления, подшипники скольжения валов и др., могут сопровождаться возникновением сложных и плохо контролируемых, а значит, и таких трудно устранимых явлений, как фрикционные автоколебания. Результатом фрикционных автоколебаний в машинах является снижение показателей качества технологических процессов, точности позиционирования, усталостные разрушения и повышенные износы деталей.
Причиной возникновения фрикционных автоколебаний является нелинейная «падающая» характеристика силы сухого трения от скорости относительного скольжения контактирующих поверхностей. [1–5, 9–11]. В этой связи определение динамических, то есть постоянно изменяющихся во времени и в функции других величин, параметров сухого некулонова трения носит важный и актуальный характер. Решение этой задачи позволит эффективнее осуществлять диагностику трущихся и контактирующих узлов машин, делать надежный прогноз динамического поведения их кинематических пар, например, прогнозирование фрикционных автоколебаний, а также обеспечит возможность целенаправленного управления процессом трения. Идентифицируемые параметры действующих нелинейных сил сухого трения могут быть использованы в качестве диагностических признаков для оценки технического состояния такого класса объектов, в том числе на дихотомическом уровне («годен» – «негоден»).
Однако непосредственное измерение действующих сил сухого трения возможно лишь триботехническими методами и подходами и весьма сложно реализуемо в упругих колебательных системах. Поэтому для идентификации динамических параметров сухого трения приходится использовать косвенные методы, основанные на измерении колебательного отклика в динамической системе.
Рассмотрим один из предлагаемых методов идентификации параметров сухого некулонова трения, реализуемый при исследовании фрикционных автоколебаний.
Расчетная динамическая схема рассматриваемой системы представлена на рис. 1.
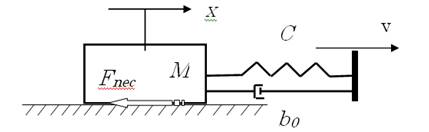
Рис.1. Расчетная динамическая схема системы для исследования фрикционных автоколебаний
Дифференциальное уравнение динамики данной системы имеет вид:
![]() , (1)
, (1)
где C – коэффициент жесткости упругого элемента;
b0 – коэффициент вязкого сопротивления;
v=const – постоянная скорость перемещения правого конца упругого элемента;
![]() (2)
(2)
- закон изменения силы сухого некулонова трения с падающей характеристикой от скорости (рис. 2).
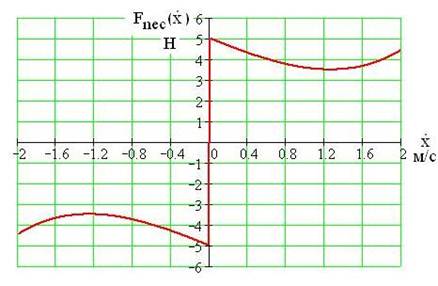
Рис.2. График зависимости силы сухого некулонова трения от скорости относительного скольжения ( F0=5 (Н); b1=1.8![]() , b3=0.38(
, b3=0.38(![]() )
)
Для компьютерного моделирования уравнения (1) с учетом (2) и исследования особенностей данной динамической системы была разработана программа в среде блочного имитационного моделирования динамических систем Simulink/MATLAB [6]. Всестороннее тестирование программы показало, что разработанный вычислительный комплекс позволяет адекватно описывать динамические процессы фрикционных автоколебаний. Особо важным и сложным при моделировании является обеспечение соответствующего характера изменения силы сухого некулонова трения на этапах скольжения и относительного покоя поверхностей трения, а также определение момента смены одного этапа другим (рис. 3).
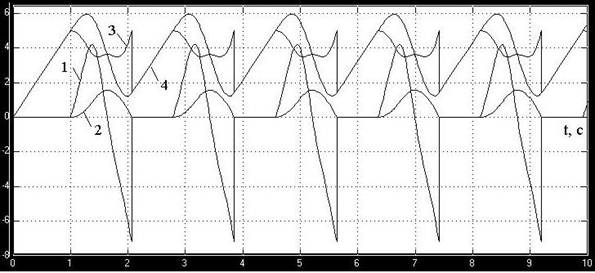
Рис. 3 Графики изменения ускорения (1), скорости (2), силы сухого некулонова трения (3) и упругой силы в пружине (4) во времени
Выполненные исследования показали, что идентификацию искомых параметров силы сухого некулонова трения с падающим участком от скорости в соответствие с принятой моделью её аппроксимации (2) возможно осуществить из анализа зафиксированных виброграмм возникающих фрикционных автоколебаний.
Для этого устанавливают регрессионную зависимость (рис. 4) суммы синхронизированных по времени сигналов, соответствующих силам упругости пружины и силам инерции, от скорости тела, совершающего фрикционные автоколебания. Указанная сумма представляет собой не что иное, как силу сухого некулонова трения, а её зависимость от скорости определяет закон изменения этой силы, коэффициенты аппроксимации которой необходимо установить.
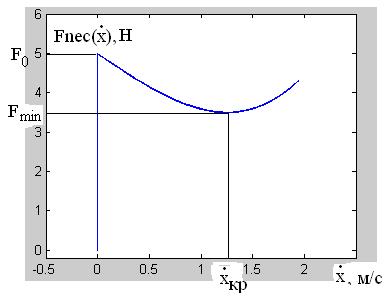
Рис. 4. Восстановленная зависимость силы сухого некулонова трения от скорости скольжения
Далее по восстановленной зависимости ![]() рассчитывают искомые коэффициенты аппроксимации F0, b1, b3:
рассчитывают искомые коэффициенты аппроксимации F0, b1, b3:
![]() ;
;

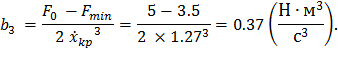
Сопоставление идентифицированных параметров силы сухого некулонова трения с падающей характеристикой от скорости с принятыми в модели показывает, что относительные погрешности предлагаемого алгоритма не превышают 3 %. Однако реальные ошибки идентификации параметров силы сухого некулонова трения будут определяться с учётом погрешностей измерения, регистрации и построения экспериментальной зависимости ![]() .
.
Экспериментальная проверка предложенного метода вибродиагностики параметров сухого некулонова трения была реализована на специально разработанном стенде (рис. 5) для исследования динамических характеристик некулонова трения [7,8].
Для измерения, преобразования и оцифровки измеряемых сигналов используется модуль с предварительным усилителем ZET 411 и аналого-цифровым преобразователем «ZET 210 Sigma USB», которые, в свою очередь, передают информационный сигнал в компьютер. В компьютере необходимо инициализировать программное обеспечение, обеспечивающее получение, хранение, визуализацию и обработку измеряемых сигналов. Далее зарегистрированные сигналы передаются в математические пакеты «MatLab» и «MathCAD», в которых происходит дальнейшая их обработка. Интерфейс программы сбора и предварительной обработки информации виден на рис.5.

Рис.5. Внешний вид испытательного стенда и программно-вычислительного комплекса для обработки результатов экспериментальных исследований
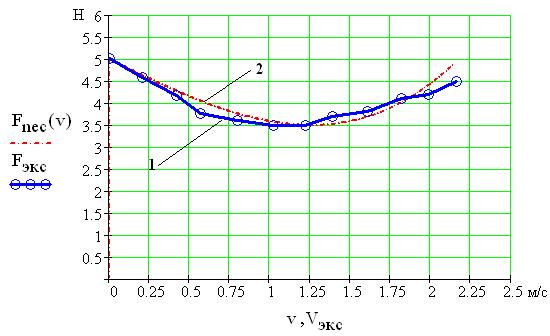
Рис. 6. Сопоставление экспериментальных результатов (кривая 1) и результатов математического моделирования (кривая 2) для графиков зависимости силы сухого некулонова трения
Анализ получаемых результатов показывает, что относительные погрешности идентификации параметров силы сухого некулонова трения в эксперименте не превысили 10-12 %: F0 =5.01 (Н), b1=0.192 ![]() , b3 =0.34 (
, b3 =0.34 (![]() .
.
Таким образом, предложенная методика, испытательный стенд и аппаратурно-вычислительный комплекс для исследования динамики фрикционных автоколебательных процессов позволяют проводить идентификацию динамических параметров силы сухого некулонова трения и реализовывать на этой основе процедуры вибрационной диагностики различных пар трения, предрасположенных к возникновению фрикционных автоколебаний.
Рецензенты:
Кобелев Н. С., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжения и вентиляция»
Юго-Западного государственного университета, г. Курск.
Локтионова О. Г., д.т.н., профессор, начальник Управления подготовки и аттестации кадров высшей квалификации Юго-Западного государственного университета, г. Курск.



