Введение
Выравнивание нуклеотидных последовательностей – одна из наиболее фундаментальных задач биоинформатики. Эта задача используется при определении сходства нуклеотидных последовательностей, при определении расстояния между последовательностями, при построении филогенетических деревьев и др. Во многих прикладных задачах возникает потребность в обработке нуклеотидных последовательностей большой длины или одновременном выравнивании многих пар последовательностей или во множественном выравнивании. Решение этих задач сдерживается длительностью их решения, что приводит к потребности разработки новых более быстрых алгоритмов, в частности, использующих технологии параллельных вычислений.
Одним из алгоритмов для выполнения глобального выравнивания нуклеотидных последовательностей является алгоритм Нидлмана-Вунша [1]. В основе алгоритма лежит идея применения метода динамического программирования [5]. Один из недостатков динамического программирования заключается в том, что таблицы ДП используют память размера О(nm) для последовательностей длины n и m. Таким образом, ограничивающим ресурсом в задаче глобального выравнивания нуклеотидных последовательностей является память. Ограничение памяти затрудняет обработку больших строк, поэтому очень важно иметь методы, уменьшающие затраты памяти без критического увеличения времени счета.
Хиршберг предложил алгоритм, значительно сокращающий затраты памяти [6]. Этот алгоритм применяется во многих задачах динамического программирования. Алгоритм Хиршберга позволяет вычислять оптимальное выравнивание строк длины n и m, используя O(n+m) количество памяти, но примерно вдвое большее время счета по сравнению с алгоритмом Нидлмана-Вунша.
В данной работе рассмотрен последовательный алгоритм, более быстрый, чем алгоритм Хиршберга, использующий память, не превышающую заранее заданного объема, и допускающий распараллеливание. Этот алгоритм основан на комбинации алгоритмов Хиршберга и Нидлмана-Вунша. Распараллеливание рассматривается двоякое: распараллеливание используемой части алгоритма Хиршберга и параллельное выполнение нескольких вызовов процедуры алгоритма Нидлмана-Вунша над различными данными. Данный алгоритм ориентирован на вычислительные архитектуры с общей памятью. Ожидается, что данный алгоритм окажется эффективным для процессоров ManyCore.
Постановка задачи
Требуется выравнивать ДНК последовательности, состоящие из четырех типов символов, соответствующих нуклеотидам (азотистым основаниям):
- A – А: Аденин;
- G – Г: Гуанин;
- C – Ц: Цитозин;
- T – Т: Тимин.
Выравнивание состоит во вставке пробелов в каждую из последовательностей. Качество выравнивания оценивают численно, назначая штрафы за несовпадение букв и за наличие пробелов, которые вставляются в последовательности для того, чтобы получить наибольшее число совпадающих позиций. Для оценки несовпадений элементов последовательностей используется матрица сравнения. Выбор матрицы оказывает большое влияние на получаемые результаты, т. к. каждая матрица представляет отражение отдельных эволюционных гипотез. В настоящее время используются серии белковых матриц Blosum, PAM и Gonnet. Для оценки выравнивания последовательностей в данной работе использована матрица сравнений Blosum 45 [2], вида:

Алгоритм
Основным прототипом предлагаемого в данной работе алгоритма является рекурсивный алгоритм Хиршберга, который отличается объемом использованной памяти, линейно зависящим от длины входных последовательностей [3], [7]. Суть алгоритма Хиршберга в том, что одна из двух входных последовательностей разбивается на две части и исходная задача сводится к двум (меньшим) задачам выравнивания второй входной последовательности с каждой из частей. Решение каждой меньшей задачи осуществляется путем аналогичного сведения к подзадачам. Алгоритм Хиршберга, как и алгоритм Нидлмана-Вунша, основан на методе динамического программирования. В терминах таблицы динамического программирования верхняя задача решается в прямоугольнике А исходной таблицы, показанной на рис. 1, нижняя – в прямоугольнике В. Верхняя задача заключается в выравнивании строки с длинами не больше n/2 и k*, а нижняя – с длинами не больше n/2 и m-k*. Для разбиения каждой задачи на подзадачи необходимо вычислить значение k*, при этом используется объем памяти, линейно зависящий от m.
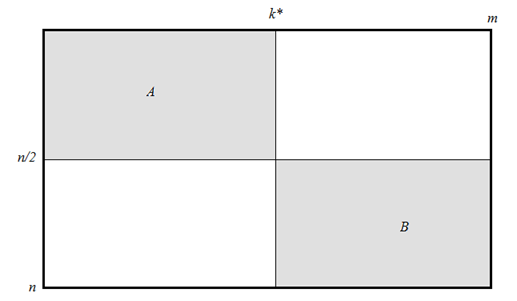
Рис. 1 Таблица динамического программирования в алгоритме Хиршберга
Алгоритм Хиршберга модифицирован путем замены рекурсии обходом бинарного дерева [4]. Узлам дерева соответствуют подзадачи, которые заключаются в выравнивании меньших подпоследовательностей и возникают в процессе решения исходной задачи. Каждый узел дерева хранит в памяти границу прямоугольной области, в которой решается соответствующая задача динамического программирования, а также некоторую другую необходимую информацию. Дерево в процессе работы алгоритма строится по уровням. Вначале оно состоит только из корневого узла, который соответствует прямоугольнику [0,0]x[m,n]. Создание двух узлов эквивалентно разбиению задачи на две подзадачи и разделению прямоугольника в терминах таблицы ДП на два, меньшего размера. Длина каждой стороны такого прямоугольника не должна быть меньше одной ячейки в таблице ДП.
Алгоритм Хиршберга заключается в обходе полного дерева всех подзадач. В данной работе по алгоритму Хиршберга выполняется обход (решение подзадач) только части вершин дерева: тех, которые удалены от корня на величину, не превосходящую заранее заданную пользователем константу h – максимальную глубину обхода дерева. При достижении глубины дерева h или минимального размера прямоугольника применяется алгоритм Нидлмана-Вунша (который работает вдвое быстрее алгоритма Хиршберга). Выбор константы h позволяет достичь максимального быстродействия при ограничениях на используемую память. Дополнительное ускорение достигается за счет распараллеливания. При тестировании глубина дерева была установлена равной 10.
Численный эксперимент
Нами написана программа оптимального глобального выравнивания нуклеотидных последовательностей на языке С. Для выполнения выравнивания программа получает на вход два файла, содержащих исходные последовательности. В результате применения данной программы строки с добавленными в них пробелами записываются в новые файлы.
В программе использованы распараллеливающие конструкции OpenMP [8]. Использование структуры данных дерева позволило параллельно решать задачи для всех узлов из одного уровня. Распараллеливание также использовано при решении каждой из подзадач, при вычислении значения k*. Это позволило эффективно использовать несколько ядер на начальных этапах алгоритма, где малое количество узлов дерева в слое не позволяет использовать более крупнозернистый параллелизм. В программе глобального выравнивания нуклеотидных последовательностей, основанной на данном алгоритме, оптимизировано использование памяти компьютера.
Были проведены эксперименты, результаты которых представлены в табл. 1.
Таблица 1
|
Длина строк |
Время (мм:сс) |
Память (МБ) |
||
|
Последовательная программа |
Параллельная программа |
Последовательная программа |
Параллельная программа |
|
|
1700/1600 |
0 |
0 |
0.8 |
1.6 |
|
1900/1600 |
0 |
0 |
0.8 |
2.5 |
|
150000/115000 |
2:33 |
1:39 |
16.8 |
16.4 |
|
360000/299000 |
15:19 |
9:54 |
43 |
61 |
|
589000/502000 |
42:55 |
27:28 |
67 |
62 |
Тестовая система: Intel Core 2 Duo T7300 (2.0 GHz, 4 MB Cache, 2 cores), 2 GB memory
По результатам численного эксперимента, приведенным в таблице 1, видно, что используемая память растет линейно с ростом длины выравниваемых строк, распараллеливание сокращает время работы примерно на 40 %.
Работа поддержана ФЦП «Научные и научно-педагогические кадры инновационной России», по теме «Создание биоинформационной технологии поиска взаимосвязанных сценариев организации в геномах животных и человека некодирующей ДНК и кодирующей белок ДНК», государственный контракт № 14.740.11.0006 от 1 сентября 2010.
Рецензенты:
Ильичев Виталий Григорьевич, доктор технических наук, главный научный сотрудник, Учреждение Российской академии наук Институт аридных зон Южного научного центра, г. Ростов-на-Дону.
Чернов Андрей Владимирович, доктор технических наук, доцент, заведующий кафедрой «Прикладной математики и вычислительной техники» ФГБОУ ВПО «Ростовский государственный строительный университет» (РГСУ), г. Ростов-на-Дону.
Кирьянов Борис Фёдорович, доктор технических наук, профессор, профессор кафедры прикладной математики и информатики, ФГБОУ ВПО Новгордский государственный университет им. Ярослава Мудрого, г. Великий Новгород.



