Введение
Квантово-механические явления играют в последнее время все возрастающую роль в области представления и обработки информации, так как размеры транзистора приблизились к нанометрическому уровню. Стремительный прогресс компьютерных технологий должен сопровождаться соответствующим развитием методов проектирования. Это позволит в полной мере использовать потенциал возможностей все более усложняющихся аппаратных средств и одновременно адаптировать их для решения вполне определенных задач. При рассмотрении современных тенденций в области компьютерных технологий в качестве отправной точки следует использовать такие устоявшиеся классические понятия, как виртуализация аппаратных средств, иерархические программы, типы данных, управление памятью, поток управление и др., которые остаются применимыми и для представления новых подходов (например, квантовые вычисления).
Рассмотрение неклассических подходов (алгоритмов) для определения новых способов решения задач в принципиально иной аппаратной среде строится на основе замены и адаптации традиционных концептуальных положений. Для представления явления с конечным числом состояний привлекается модель квантовых цепей [7].
Вопрос об увеличении мощности вычислений по сравнению с классическим компьютером рассмотрен в 1992 г. в работах Deutsch D. и Jozsa R. [6], а также Berthiaume A. и Brassard G. [5]. Они показали, что имеются задачи, эффективно решаемые на основе квантовых подходов (асимптотически быстрее, чем классически). Отметим, что примеры задач несколько искусственные (без практической применимости), но позволяют представить суть подхода и проводить реальные физические эксперименты по их реализации.
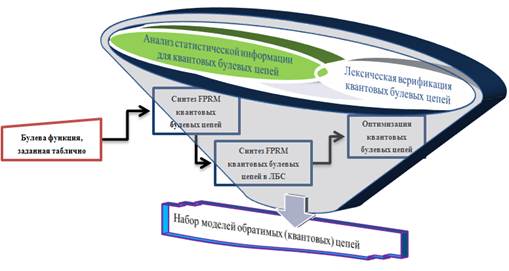
Рисунок 1. Фрагмент применяемого маршрута проектирования квантовых булевых цепей
При проектировании [4] обратимых и квантовых цепей может быть использован класс квантовых цепей (квантовые булевы цепи) с логикой на базе AND/EXOR, которая на основе полиномиальных нормальных форм позволяет получить представление булевых функций меньшей сложности и упростить верификацию синтезированных цепей. В статье рассмотрен пример построения набора квантовых булевых цепей, синтезированных на основе поляризованных полиномов Рида – Маллера (FPRM) с выбором оптимальных полиномиальных форм на основе предварительного статистического анализа определенных характеристик FPRM всех полярностей. Фрагмент применяемого маршрута проектирования квантовых булевых цепей представлен на рис. 1.
FPRM-представление [1] булевых функций (n входов и 1 выход) – это «сложение по модулю 2» EXOR от AND минитермов, в которых каждая булева переменная либо в прямой, либо в инверсной форме, но не в обеих: 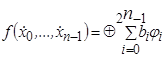 , где
, где 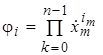 ,
, ![]() или
или ![]() и xm, bi Î{0, 1} и im представляют собой двоичные числа в m; ji известны как произведения термов, а bi определяет, представлено произведение термов или нет. Символ Å обозначает операцию EXOR и символ умножения – точка обозначает операцию AND.
и xm, bi Î{0, 1} и im представляют собой двоичные числа в m; ji известны как произведения термов, а bi определяет, представлено произведение термов или нет. Символ Å обозначает операцию EXOR и символ умножения – точка обозначает операцию AND.
Описание решения
Рассмотрим этап синтеза, на котором по заданной таблице истинности для n булевых переменных строится поляризованный полином Рида – Маллера (нулевой полярности) и формируется набор поляризованных полиномов FPRM фиксированной полярности (от 1 до 2n – 1). На основе полученных полиномов в нотации Рида – Маллера генерируются наборы квантовых булевых схем в нотации квантовых преобразователей. Преобразователь NOT инвертирует входной кубит, что реализуется операцией EXOR с логической 1. Преобразователь CNOT инвертирует целевой кубит, если управляющий кубит в 1, при этом выполняется операция EXOR для обоих кубитов. Преобразователь Тоффоли инвертирует целевой кубит, когда оба управляющих кубита имеют значение 1, что реализуется операциями EXOR для целевого кубита и AND для обоих управляющих кубитов. Синтез соответствующей квантовой цепи осуществляется на основе сопоставления фрагментов FPRM представления и нотации квантовых преобразователей. Матричная запись и программная реализация графического представления библиотеки базовых квантовых преобразователей имеет следующий вид (символ ![]() в графической нотации обозначает операцию EXOR, а символ
в графической нотации обозначает операцию EXOR, а символ ![]() – управляющий кубит):
– управляющий кубит):
а) преобразователь NOT ![]() для кубита имеет вид:
для кубита имеет вид: ![]() ;
;
б) преобразователь C1NOT ![]() для двух кубитов имеет вид:
для двух кубитов имеет вид:
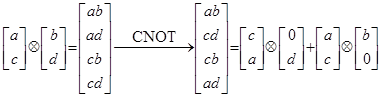 ;
;
в) преобразователь C2NOT (Тоффоли) 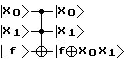 для трёх кубитов имеет вид:
для трёх кубитов имеет вид:
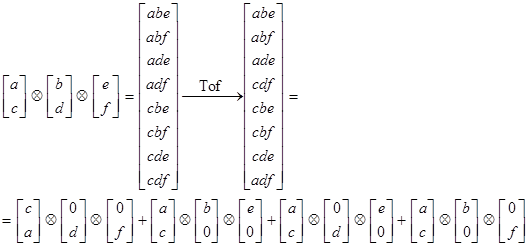 ;
;
г) преобразователь SWAP для двух кубитов ![]() имеет вид
имеет вид
 .
.
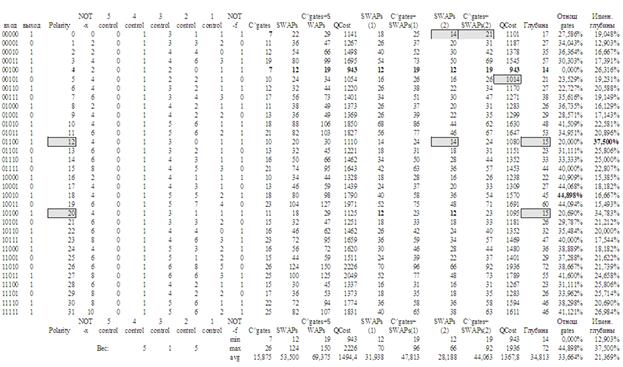
Рисунок 2. Таблица истинности пяти переменных
Рассмотрим пример построения набора квантовых цепей для булевой квантовой функции по заданной таблице истинности 5 переменных на основе анализа характеристик квантовых цепей (рис. 2). По таблице истинности проводится последовательный синтез логической функции в нотациях полиномов FPRM с последующей трансляцией в нотацию квантовой цепи. В итоге автоматически генерируется набор эквивалентных квантовых цепей, которые имеют разный состав (качественный и количественный) преобразователей. Задача синтеза и оптимизации квантовой цепи может быть сведена к традиционным логическим решениям на основе полиномов FPRM различной полярности. Полином 0-й полярности имеет вид: ![]() .
.
Результаты первичного синтеза и анализа цепей автоматически передаются в Excel (рис. 2) с формированием столбцов: «Polarity» – номер полярности, «NOT-x» – количество преобразователей NOT для обращаемых кубитов ![]() , где n – число управляющих кубитов, столбцы k-control (число kÎ{1, n}) – количество CkNOT, «NOT-f» – количество NOT, воздействующих на функциональный кубит
, где n – число управляющих кубитов, столбцы k-control (число kÎ{1, n}) – количество CkNOT, «NOT-f» – количество NOT, воздействующих на функциональный кубит ![]() , «gates» – количество преобразователей в цепи, «SWAPs» – количество преобразователей SWAP, необходимых для приведения преобразования цепи с точки зрения близкого соседства без учета возможной оптимизации, «gates+SWAPs» – количество преобразователей в цепи с учетом SWAP, «QCost» – квантовая стоимость цепи. За единицу квантовой стоимости выбран однокубитовый преобразователь, в примере – NOT. Стоимость двухкубитового преобразователя зависит от технологии его реализации и определяется на основе стандартного разложения на однокубитовые преобразователи со значением 5. Аналогично для преобразователей большей мерности. В примере для функции на рис. 2 оптимальной с точки зрения разных критериев оказалась цепь Polarity 4. По числу преобразователей также оптимальна цепь Polarity 20. По глубине (определяется по числу уровней преобразователей, где каждый уровень содержит набор тех преобразователей, которые могут быть реализованы параллельно) и квантовой стоимости – цепь Polarity 4, а по глубине к ней близки Polarity 12 и 20. Дальнейший выбор цепи будет зависеть от того, в какой технологии предполагается ее реализации, а также от типа используемой оптимизации.
, «gates» – количество преобразователей в цепи, «SWAPs» – количество преобразователей SWAP, необходимых для приведения преобразования цепи с точки зрения близкого соседства без учета возможной оптимизации, «gates+SWAPs» – количество преобразователей в цепи с учетом SWAP, «QCost» – квантовая стоимость цепи. За единицу квантовой стоимости выбран однокубитовый преобразователь, в примере – NOT. Стоимость двухкубитового преобразователя зависит от технологии его реализации и определяется на основе стандартного разложения на однокубитовые преобразователи со значением 5. Аналогично для преобразователей большей мерности. В примере для функции на рис. 2 оптимальной с точки зрения разных критериев оказалась цепь Polarity 4. По числу преобразователей также оптимальна цепь Polarity 20. По глубине (определяется по числу уровней преобразователей, где каждый уровень содержит набор тех преобразователей, которые могут быть реализованы параллельно) и квантовой стоимости – цепь Polarity 4, а по глубине к ней близки Polarity 12 и 20. Дальнейший выбор цепи будет зависеть от того, в какой технологии предполагается ее реализации, а также от типа используемой оптимизации.
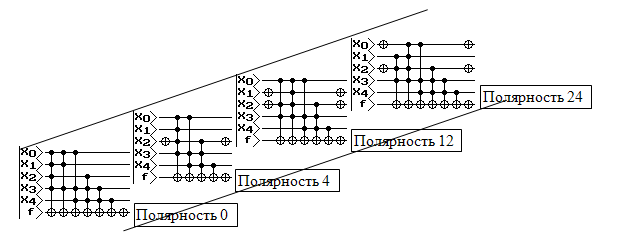
Рисунок 3. Экранные формы результата автоматического синтеза квантовых цепей
На рис. 3 представлены экранные формы результата автоматического синтеза квантовых цепей для различных полярностей полиномов Рида – Маллера с наиболее оптимальными предварительно проанализированными характеристиками – полярности 0, 4, 12 и 20.
Для физической реализации возможна дальнейшая оптимизация набора схем [2], например, с точки зрения близкого соседства в зависимости от технологии реализации. Синтез квантовых логических цепей основан на библиотеке, состоящей из NOT, CNOT, C2NOT и SWAP преобразователей. Использование SWAP-преобразователей обусловлено требованием смежности входов квантовых преобразователей в схемах близкого соседства.
Простая предварительная оптимизации с точки зрения близкого соседства рассмотрена на примере цепи нулевой полярности. В этом случае применено 18 преобразователей SWAP (рис.4, слева). Минимизация по размещению каскадных SWAP выполняется на основе анализа их типового размещения. Шаблоны замещения каскадных SWAP приведены в [3]. Многопроходная минимизация с использованием шаблонов приводит к значительному сокращению преобразователей SWAP, уменьшая общее число преобразователей квантовой цепи (рис.4, справа) и ее глубину.
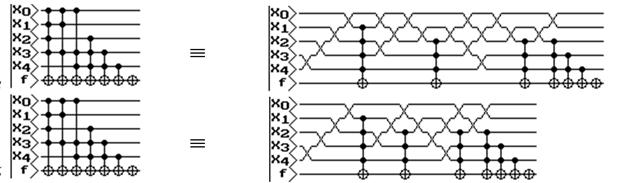
Рисунок 4. Многопроходная минимизация квантовых цепей
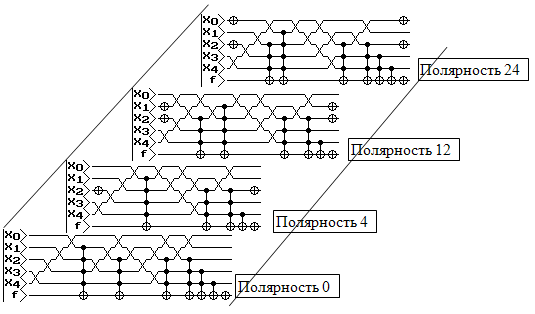
Рисунок 5. Спецификации оптимизированных квантовых цепей
Результирующие представления спецификаций после замещения каскадных SWAP для полярностей 0, 4, 12 и 20 представлены на рис. 5.
Заключение
Разработана и апробирована методика проектирования спецификаций квантовой цепи на основе таблично заданных булевых функций. Наглядно продемонстрировано, что многопроходная минимизация приводит к значительному сокращению преобразователей SWAP, тем самым уменьшая общее число преобразователей и глубину моделируемой квантовой цепи.
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009–2013 годы» (Государственный контракт № 14.B37.21.2021 от 11 ноября 2012 г.).
Рецензенты:
Водяхо Александр Иванович, д.т.н., профессор кафедры вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Пузанков Дмитрий Викторович, д.т.н., зав. кафедрой вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.



