Введение
Задачи распознавания сцен и изображений традиционно входят в число классических проблем искусственного интеллекта [3]. Причем, если решение задачи распознавания изображений обычно не вызывает серьезных трудностей [1, 2], то в распознавании сцен успехов достигнуто значительно меньше [3]. Способность определять, имеется ли на изображении тот или иной объект, важна для практики, в частности для систем видеонаблюдения. Обнаружив, что на изображении имеются люди, можно приступить к детекции и распознаванию лиц, а в случае наличия автомобилей, перейти на детекцию и распознавание автомобильных номерных знаков. Таким образом, нет необходимости постоянно отрабатывать алгоритмы для обработки объектов других видов. Когда наблюдение за территорией ведется круглосуточно, информация о наличии, либо отсутствии объекта на изображении позволит сократить время обработки изображений и избавит от лишней нагрузки на процессор, что, в свою очередь, позволит быстрее получить нужные данные. Например, можно вести учет въехавших и выехавших автомобилей на охраняемую территорию, учет отгруженных товаров и даже определять – где и в какое время находился определенный сотрудник.
Проблема заключается в том, что не существует универсальных методов определения наличия объекта на изображении. Можно лишь использовать специальные алгоритмы для поиска конкретных объектов, но и в данном случае выбор алгоритмов слишком велик и среди них нет универсального. Например, для поиска лиц существует много алгоритмов, такие как: метод главных компонент (Principal component analysis, PCA) [7], линейный дискриминантный анализ (Linear Discriminant Analysis, LDA) [7], скрытые Марковские модели [7], гибкое сопоставление (Elastic matching, EM) [7], метод опорных векторов [7] и активная модель внешнего вида (Active appearance model, AAM) [7]. И это не полный список методов поиска лиц на изображении. Более обобщенным методом поиска объектов можно считать подход «оптический поток» (Оptical flow) [8], но он годится только для движущихся объектов – в общем случае определяют направление движения объекта и уже работают с примерной формой обнаруженного объекта.
Преобразование Фурье было выбрано вместо вейвлет анализа, потому что дискретное вейвлет преобразование не сохраняет постоянство при сдвиге [6, с. 62]. У преобразования Фурье, согласно свойству сдвига во времени, спектр объекта не меняется, а меняется только фаза, поэтому спектр всегда получается один, где бы на изображении объект ни находился.
Из готовых реализаций преобразования Фурье стоит упомянуть функцию fft в пакете прикладных программ MATLAB [9] и библиотеку FFTW, написанную на С [10]. Все существующие решения не пригодны для полного исследования преобразования Фурье, и их интеграция с нашими проектами стоила бы неоправданное количество времени и сил.
Постановка задачи
Требуется исследовать различные виды преобразования Фурье, написать комплекс программ для освоения и практического применения преобразования Фурье, исследовать основные свойства преобразования Фурье на практике и выяснить, насколько возможно и практически применимо преобразование Фурье для определения наличия объектов на изображении.
Выбор типа преобразования Фурье
Из анализа литературы по вопросу преобразования Фурье следует, что многие исследователи не имеют единого мнения о предмете. Если рассматривать разных авторов, то одни и те же обозначения в формулах означают разные параметры. Из приведенных ниже формул (1) [4, с. 6], (2) [5, с. 14] и (3) [6, с. 35, с. 38] будем использовать формулу (3), чтобы избежать путаницы в обозначениях.
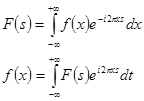 , (1)
, (1)
где ![]() – сигнал в области времени,
– сигнал в области времени, ![]() – преобразование Фурье,
– преобразование Фурье, ![]() – время,
– время, ![]() – частота,
– частота, ![]() – мнимая единица.
– мнимая единица.
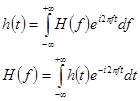 , (2)
, (2)
где функции ![]() и
и ![]() составляют пару преобразования Фурье,
составляют пару преобразования Фурье, ![]() – преобразование Фурье,
– преобразование Фурье, ![]() – сигнал в области времени,
– сигнал в области времени, ![]() – частота,
– частота, ![]() – время,
– время, ![]() – мнимая единица.
– мнимая единица.
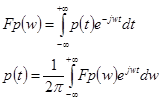 , (3)
, (3)
где ![]() – преобразование Фурье,
– преобразование Фурье, ![]() – угловая частота,
– угловая частота, ![]() измеряется в рад/с (где частота
измеряется в рад/с (где частота ![]() – обратная величина от времени
– обратная величина от времени ![]() ,
, ![]() ),
),![]() – мнимая единица,
– мнимая единица,![]() непрерывный сигнал (непрерывно изменяющийся с течением времени),
непрерывный сигнал (непрерывно изменяющийся с течением времени), ![]() .
.
Дадим краткий обзор разных видов преобразования Фурье и поясним некоторые их отличительные особенности.
Любой получаемый сигнал можно представить в виде сумм волн синусов и косинусов. Преобразование сигнала с помощью алгоритмов Фурье можно разделить на четыре категории, в зависимости от того, к какому из четырех базовых типов принадлежит этот сигнал. Сигнал может быть непрерывным или дискретным, периодическим или не периодическим. Комбинация этих двух особенностей дает в сумме четыре категории сигнала:
1. Не периодичный непрерывный. К таким сигналам относится, например экспонента и кривая Гаусса. Эти сигналы устремляются в бесконечность в обе стороны и не представляют собой совокупности повторяющихся периодов. Этот тип преобразования называют преобразованием Фурье (Fourier Transform).
2. Периодичный непрерывный. К таким сигналам можно отнести синусоиды, квадратные волны и любые волны с повторяющимся периодом от минус бесконечности до плюс бесконечности. Этот тип преобразования называют ряды Фурье (Fourier Series).
3. Не периодичный дискретный. Эти сигналы только определены дискретными точками между плюс бесконечностью и минус бесконечностью и не имеют повторяющегося периода. Этот тип преобразования называют дискретным преобразованием Фурье во времени (Discrete Time Fourier Transform).
4. Периодичный дискретный. Это дискретные периодические сигналы от минус бесконечности до плюс бесконечности. Этот тип преобразования называют дискретными рядами Фурье (Discrete Fourier Series) или дискретным преобразованием Фурье (Discrete Fourier Transform).
Заметим, что в каждой категории преобразования Фурье сигналы изменяются от минус бесконечности до плюс бесконечности. На практике приходиться работать с дискретными сигналами конечной длины. Так как волны синуса и косинуса определены от минус бесконечности до плюс бесконечности, то невозможно, используя группу бесконечно длинных сигналов, создать что-то конечной длины. Чтобы обойти эту проблему, нужно вообразить, что наш сигнал имеет бесконечное число точек слева и справа от наших реальных данных. Если все эти воображаемые точки имеют значение ноль, то сигнал выглядит как дискретный не периодический, тогда применяется дискретное преобразование Фурье во времени. Если наши воображаемые точки будут копиями исходных N точек сигнала, то сигнал будет выглядеть дискретным периодическим с периодом в N точек. В этом случае применяется дискретное преобразование Фурье (ДПФ).
Чтобы создать не периодический сигнал, необходимо бесконечное число синусоид, поэтому вычислить дискретное преобразование Фурье во времени невозможно. Из вышесказанного, можно сделать вывод, что на практике, с помощью компьютеров, можно использовать только дискретное преобразование Фурье, потому что электронные вычислительные машины работают только с информацией, которая дискретна и имеет конечную длину.
Каждая категория преобразования Фурье разбивается на два вида: в вещественных числах и в комплексных числах. Категория в комплексных числах более сложна для восприятия, но именно на ней основано быстрое преобразование Фурье (БПФ), которое повсеместно и применяется для обработки цифровых сигналов.
Преобразование Фурье для получения спектра изображения
Любое изображение представляет собой двумерный сигнал. Для получения спектра изображения надо взять одномерное преобразование Фурье от каждой строки изображения, а после проделать то же самое с каждым столбцом из полученных данных. Для этой работы необходимо использовать БПФ, так как простое ДПФ слишком медленно обрабатывает изображения, и его стоит применять только лишь для одномерных сигналов, не превышающих 32 точки.
Опишем некоторые свойства преобразования Фурье, которые нам понадобятся для интерпретации спектра изображений.
1. Линейность. Если складывать или вычитать два сигнала в области времени, то их спектры также складываются или вычитаются. Это означает, что можно раскладывать изображения по спектру. Например, имеется в наличие кровавый отпечаток на ткани. Очень сложно отделить отпечаток от ткани, анализируя целое изображение. Однако если с помощью преобразования Фурье перевести изображение в область частот, то будут получены как сильные компоненты, представляющие текстуру ткани, так и слабые разбросанные компоненты, представляющие отпечаток. Если подавить частотные компоненты ткани и провести обратное преобразование Фурье, то ткань исчезнет с изображения и останется только отпечаток пальца, который можно легко рассмотреть [6, с. 57].
2. Сдвиг во времени. Это означает, что при смещении сигнала в области времени, его спектр не изменяется, меняется только фаза.
3. Поворот. Это означает, что при повороте сигнала в области времени, сигнал в области частот поворачивается точно также.
4. Масштабируемость. Это означает, что при расширении сигнала в области времени, его спектр становится уже и наоборот.
Поясним, что представляет собой спектр изображения. В спектре сигнала низкочастотные компоненты показывают те части изображения, где яркость практически не меняется. Высокочастотные компоненты показывают изменения в интенсивности. Таким образом, если оставить только низкие частоты (низкочастотный фильтр), то после обратного преобразования Фурье будут получены лишь расплывчатые пятна. Если же оставить только высокие частоты (высокочастотный фильтр), то останутся в основном только контуры предметов, так как именно на их границах резко меняется яркость изображения.
Поясним, как некоторые свойства преобразования Фурье влияют на изображения.
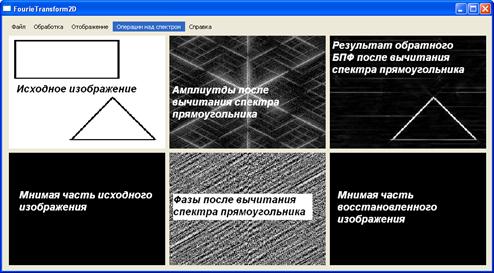
Рисунок 1. Вычитание спектра прямоугольника из изображения
Согласно свойству Фурье, «сдвиг во времени» при смене положения объекта на изображении, в области частот меняется только фаза, таким образом, по амплитуде можно понять, что это именно этот объект, пусть даже находящийся в другом месте на изображении. Если же на изображении имеется множество разных объектов, то их спектры сложатся, и будет невозможно узнать, присутствовал ли на изображении искомый объект. Разумеется, согласно свойству линейности, можно из спектра изображения вычесть спектр искомого объекта (рисунок 1). Тогда, если объект на изображении присутствовал, то он исчезнет с изображения. Если на изображении искомого предмета не было, то результат будет зависеть от того, как много частот занимает вычитаемый объект. А именно, либо будут небольшие помехи на изображении, либо изображение станет неразборчивым (рисунок 2).
Поясним рисунок 1. На исходном изображении расположены два объекта – прямоугольник и треугольник, на белом фоне. Используя прямое преобразование Фурье, был получен спектр изображения и из него был вычтен спектр прямоугольника на белом фоне. Над полученным спектром было проведено обратное преобразование Фурье. Его результат помещен в правую часть рисунка 1. После выполнения обратного преобразования Фурье цвет треугольника изменился с черного на белый, потому что в спектре вычитаемого прямоугольника содержался также и белый фон, который и был вычтен из изображения, поэтому вместо вещественной части были представлены амплитуды восстановленного сигнала. Мнимые части отображены черным цветом, потому что они равны нулю. Отсутствие прямоугольника на восстановленном изображении показывает, что вычитание спектров проведено успешно, и таким образом это означает, что прямоугольник присутствовал на исходном изображении.
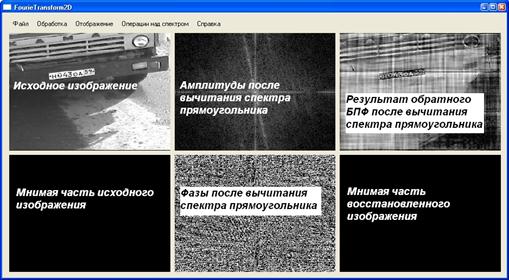
Рисунок 2. Вычитание спектра прямоугольника из изображения, где прямоугольник не присутствовал
Все приведенные выше операции проводились с помощью созданного в процессе исследования комплекса программ.
Вывод
С помощью разработанного комплекса программ были проведены исследования основных свойств преобразования Фурье (сдвиг, масштабирование, линейность, поворот) на различных изображениях, и теперь можно с достаточной долей уверенности заявить, что для изображений реального мира с помощью преобразования Фурье определить наличие или отсутствие объекта на изображении невозможно, так как при вычитании спектра несуществующего объекта на изображении, на изображении появятся помехи, и их количество зависит от того, как много частот занимал вычитаемый объект. Поэтому вопрос о том, каким универсальным способом можно определить наличие или отсутствие тех или иных объектов на изображении, остается не решенным.
Рецензенты:
Пенский Олег Геннадьевич, доктор технических наук, доцент, профессор кафедры процессов управления и компьютерной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.
Ясницкий Леонид Нахимович, доктор технических наук, профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический универ-ситет, г. Пермь.



