Введение
Электротехнологией следует считать область промышленной технологии, в которой электрические и магнитные явления используются для непосредственного воздействия на обрабатываемый объект. При этом индукционным нагревом называют электротехнологические процессы передачи энергии обрабатываемому объекту за счет явления электромагнитной индукции [5].
Индукционный нагрев металлов, применяемый в промышленных установках с конца XIX в., в настоящее время получил широкое распространение во многих областях промышленности. Причиной такого успеха индукционного нагрева являются достоинства, присущие этому виду нагрева [2]. Широкое применение индукционного нагрева для различных видов термообработки изделий требует простых методов проектирования специальной аппаратуры, к которой, прежде всего, относятся индукторы, служащие для концентрирования переменного электромагнитного поля в нагреваемых зонах [3].
В настоящее время развивается направление, которое предусматривает использование одной и той же установки для комплексного электротехнологического процесса. Кроме того, при больших мощностях, наряду с высокочастотным индукционным нагревом, достаточно широко распространен нагрев при промышленной частоте 50 Гц. Примером такого устройства, является установка для нанесения защитных (цинковых) покрытий на детали, находящиеся внутри реторты, представляющей собой полый цилиндр, сделанный из немагнитной жаропрочной стали.
В связи с этим возникает необходимость разработки комплексных электротехнологических установок для нагрева деталей и одновременного нанесения на них защитных (цинковых) покрытий. Для достижения данной цели необходимо решить ряд задач, таких как:
1. Расчет параметров электромагнитного поля в системе индуктор – полый цилиндр (реторта) – деталь;
2. Построение схемы замещения данной установки, учитывающей влияние реторты на распределение магнитного поля в детали, обеспечивающего нагрев деталей.
3. Определение основных соотношений, используемые при расчете и проектировании данных установок для нагрева деталей и нанесения на них защитных (цинковых) покрытий.
Расчет параметров электромагнитного поля необходим для подтверждения возможности индукционного нагрева деталей, находящихся внутри стальной реторты, а также для определения значений напряженностей магнитного (H) и электрического (E) полей, плотностей тока (δ) на элементах, подвергающихся индукционному нагреванию.
При анализе электромагнитных процессов приняты следующие допущения:
1. Индуктор, реторта и деталь являются бесконечно длинными;
2. Реторта и детали изготовлены из немагнитной стали, т.е. их соответствующие относительные магнитные проницаемости μрет, и μдет равны единице;
3. Удельные электрические сопротивления реторты и деталей ρрет и ρдет, а также их магнитные проницаемости постоянны по сечениям реторты и деталей;
4. Напряженности магнитного и электрического полей реторты и деталей направлены вдоль их осей, и при условии допущения 1 и осевой симметрии реторты и деталей, можно считать, что эти напряженности зависят только от радиусов R реторты и деталей [4].
5. Технологический процесс является квазистационарным гармоническим, т.е. напряженность магнитного поля H=Hm•e jωt; где Hm – амплитудное значение напряженности магнитного поля; угловая частота ω=2•π•f; f = 50 Гц – частота тока; t – время [1].
6. Тангенциальная составляющая напряженности магнитного поля не претерпевает скачка на границе раздела сред. Следовательно, напряженность поля в воздушном зазоре между индуктором и ретортой HВ одновременно является и напряженностью магнитного поля на поверхности обмотки индуктора HИ, а также на внешней поверхности реторты Hm0, т.е. HИ = Hm0 [4]. Напряженность магнитного поля на внутренней поверхности реторты Hm3 равна напряженности магнитного поля во всех точках внутренней полости реторты. Напряженность магнитного поля во внутренней полости реторты равна напряженности на внешней поверхности детали Hm4.
Расчет параметров электромагнитного поля комплексной электротехнологической установки
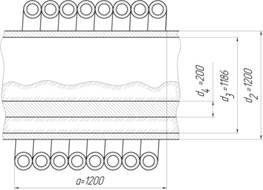
На рис. 1, а приведена электромагнитная система разрабатываемой комплексной электротехнологической установки, состоящая из индуктора и реторты, при отсутствии нагреваемых деталей. На рис. 1, б приведена электромагнитная система разрабатываемой установки при наличии нагреваемых деталей. Для упрощения расчетов представим все металлические детали в виде единого сплошного металлического цилиндра, диаметром d4=0,2 м. Примем следующие параметры: длина индуктора a=1,2 м (рис. 1, а), наружный радиус реторты R2=0,6 м, внутренний радиус реторты R3=0,593 м.
а)
б)
Рис. 1. Электромагнитная система: а) При отсутствии деталей; б) При наличии деталей
Рассчитаем значение напряженности магнитного поля на внутреннем радиусе реторты.
При решении задачи исходными уравнениями являются основные уравнения электромагнитного поля – уравнения Максвелла. В общем случае для проводящей среды эти уравнения имеют вид:
(1)
(2)
где δ – плотность тока проводимости, А/м2; 
– вектор электрического смещения, Кл/м2; 
– вектор индукции магнитного поля, А/м.
Уравнения (1) и (2) в цилиндрических координатах для H, E=f(R) имеют следующий вид:
(3)
(4)
где γ – удельная проводимость, См/м; μ0 – магнитная постоянная, Гн/м; μ – относительная магнитная проницаемость.
Исключая 
из уравнения (4), получим
(5)
Выражение (5) можно переписать в следующем виде
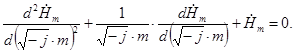(6)
Дифференциальное уравнение (6) является частным случаем уравнения Бесселя – уравнением Бесселя нулевого порядка от комплексного аргумента 
, где m – относительный радиус.
Решая уравнение (6) для радиусов реторты Rрет=R2÷R3 можно получить выражение для напряженности магнитного поля на внутренней поверхности реторты
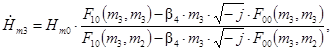(7)
где Hm0 – напряженность магнитного поля на поверхности индуктора, А/м; 
m3 – относительный внутренний радиус реторты; N1 – символ функции Бесселя второго рода, первого порядка; J0 – символ функции Бесселя первого рода, нулевого порядка; J1 – символ функции Бесселя первого рода, первого порядка; N0 – символ функции Бесселя второго рода, нулевого порядка; 
m2 – относительный наружный радиус реторты; 
Решая уравнение (6) для зоны, ограниченной нагреваемой деталью, диаметром d4, можно получить выражение для напряженности магнитного поля в детали
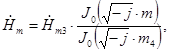(8)
где m4 – относительный наружный радиус детали.
Решая уравнения (6) совместно с (3), можно получить выражение для напряженности электрического поля в детали
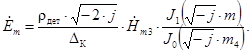(9)
где ρдет – удельное электрическое сопротивление материала детали, Ом·м;
ΔК – горячая глубина проникновения тока в материал детали, м;
Решая уравнения (6) совместно с (3), можно получить выражение для плотности тока в детали
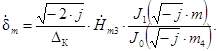(10)
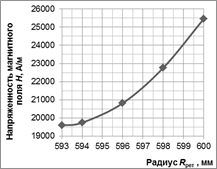
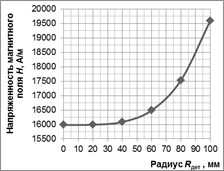
Значения напряженности магнитного поля в толще полого цилиндра (реторты), значения напряженностей магнитного и электрического полей, а также плотности тока в детали рассчитаны в пакете Mathematica при различных радиусах R сечения реторты и детали. По результатам расчетов построены графики, представленные на рис. 3, 4.
а)
б)
Рис. 3. Результаты расчетов напряженностей электромагнитного поля: а) Распределение напряженности магнитного поля по сечению реторты; б) Распределение напряженности магнитного поля по сечению детали;
а)
б)
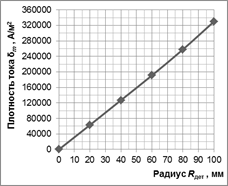
Рис. 4. Результаты расчетов напряженностей электромагнитного поля и плотности тока:
а) Распределение напряженности электрического поля по сечению детали; б) Распределение плотности тока по сечению детали
Построение схемы замещения комплексной электротехнологической установки
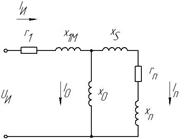
Для подробного расчета параметров данной установки необходимо составить ее полную электрическую схему замещения, учитывающую влияние реторты на параметры электромагнитного поля. Полная схема замещения данной установки представлена на рис. 5, а. Для возможности дальнейшего полного расчета параметров данной установки заменим ветви реторты и нагрузки общей ветвью с сопротивлениями rn, xn (рис. 5, б).
а)
б)
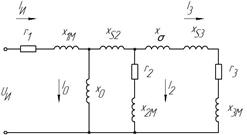
Рис. 5. Схема замещения комплексной электротехнологической установки: а) Полная схема замещения установки; б) Схема замещения установки с общей нагрузочной ветвью
В полной схеме замещения данной установки (рис. 5, а) IИ – ток, потребляемый индуктором, I3 – ток, протекающий в детали, UИ – напряжение на индукторе, I0 – ток в цепи обратного замыкания магнитного потока, I2 – ток, протекающий в реторте, r1 – активное сопротивление провода индуктора, x1M – внутреннее реактивное сопротивление индуктора, xS2 – реактивность рассеяния реторты, xσ – реактивное сопротивление, учитывающее ослабление магнитного поля, проникающего через реторту к детали, xS3 – реактивность рассеяния детали, x0 –реактивное сопротивление обратного замыкания магнитного потока, r2 – активное сопротивление реторты, приведенное к току участка индуктора бесконечной длины, x2M – внутреннее реактивное сопротивление реторты, приведенное к току участка индуктора бесконечной длины, r3 – активное сопротивление детали, приведенное к току участка индуктора бесконечной длины, x3M – внутреннее реактивное сопротивление детали, приведенное к току участка индуктора бесконечной длины.
Сопротивления нагрузочной ветви приводятся к току индуктора с помощью коэффициента
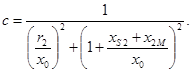(11)
Основные соотношения для расчета и проектирования комплексных электротехнологических установок
Ток в индукторе
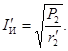(12)
Плотность тока в индукторе
(13)
где g – коэффициент заполнения.
Падение напряжения в индукторе
(14)
где zЭ – эквивалентное полное сопротивление индуктора, Ом.
Число витков индуктора
(15)
КПД индуктора
(16)
где rЭ – эквивалентное активное сопротивление индуктора, Ом.
Коэффициент мощности индуктора
(17)
Выводы
1. Применение данных установок позволяет значительно повысить энергетические и массогабаритные показатели устройств за счет совмещения двух технологических процессов в одной установке.
2. Приведенные выражения позволяют определить значения напряженностей магнитного и электрического полей, плотности тока при расчете и проектировании данных установок, применение пакетов программ, например, Mathematica, позволяет производить расчет электромагнитного поля в системе индуктор – реторта – деталь, определяемого решением уравнений Бесселя нулевого порядка от комплексного аргумента.
3. При частоте 50 Гц значение напряженности магнитного поля во внутренней полости полого цилиндра (реторты) составляет 77% от значения на поверхности реторты, в связи с чем можно говорить о целесообразности применения данных комплексных электротехнологических установок с частотой питания 50 Гц. Значение напряженности магнитного поля в центре детали составляет 82% от значения на поверхности детали, что позволяет говорить о возможности сквозного индукционного нагрева деталей в реторте.
4. Распределение напряженности электрического поля и плотности тока по сечению детали носит линейный характер. Значения напряженности электрического поля и плотности тока уменьшаются до нуля от поверхности к центру детали и для расчетов могут быть аппроксимированы прямой линией.
5. Составленная схема замещения адекватно отражает электромагнитные процессы, происходящие в данной установке, с учетом ослабления магнитного поля, проникающего через реторту к нагреваемым деталям. Приведенные соотношения (12)÷(17) могут быть использованы для расчета и проектирования данных установок.
Рецензенты:
Костюкова Татьяна Петровна, д.т.н., профессор кафедры «Экономическая информатика» ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.
Гизатуллин Фарит Абдулганеевич, д.т.н., профессор кафедры «Электромеханика» ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.