Введение
С развитием различных радиотехнических систем и усложнением решаемых ими тактико-технических задач возрастают требования к характеристикам антенн, а в ряде случаев для достижения лучших показателей необходимо применить совершенно новые виды антенн, не имеющих прямой аналогии с существующими ранее и находящимися в эксплуатации [1]. Цель статьи предложить новый подход к расчёту характеристик антенн и дать практические рекомендации по его использованию.
Практически любые приближенные методы дают точные результаты лишь в тех случаях, когда антенна расположена очень близко к поверхности с потерями. Например, в работе [9] автор утверждает, что его программа для анализа тонких штыревых антенн над плоской полупроводниковой поверхностью не может быть применена в случаях, когда высота антенны меньше длины волны. В случае применения метода изображений, в работе [3] автор делает вывод, что этот метод является очень точным для всех комбинаций исходных высоты и электрических параметров, которые имеют практическое значение, за исключением высоты меньше длины волны. Тем не менее, следует отметить, что в [4] был предложен приближенный метод быстрого решения, и это дает очень точный анализ антенн на границе поверхности раздела сред. Этот метод основан на переходе от неоднородной среды к анализу эквивалентных электрических параметров в однородной среде.
Предложенная методика уже применялась для анализа вертикальных и горизонтальных дипольных антенн (ГДА), расположенных в воздухе над однородной средой и изотропной средой с потерями [2,6-8]. Результаты этих исследований показали, что используемый метод может быть применен к анализу различных структур дипольной антенны независимо от электрических и геометрических параметров. Но, случай расположения антенны на границе раздела сред в этой статье исследуется впервые.
Теоретический подход
Рассмотрим общую задачу анализа симметричной ГДА, помещенной в воздухе на высоте, выше однородной изотропной среды (ОИС), которая рассматривается как ОИС с известными электрическими параметрами. ГДА расположена в направлении параллельном оси х, в прямоугольной декартовой системе координат, как показано на рис. 1, и запитана от идеального генератора.
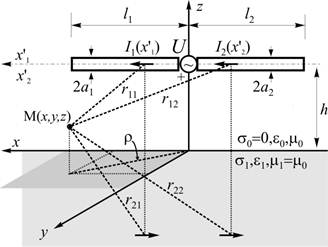
Рисунок 1 - Схематическое изображение симметричной ГДA
В случае горизонтальной структуры антенны, расположенной в воздухе над поверхностью с потерями, можно использовать выражения Герца, векторный потенциал которых [6-8] включает в себя два типа интегралов Зоммерфельда:
![]() , (1)
, (1)
![]() , (2)
, (2)
где первые множители в обоих подынтегральных выражениях представляют собой спектральные коэффициенты отражения, а ядро имеет вид зеркального отображения спектрального потенциала на плоскости. Для решения этих интегралов можно применить метод точных приближений для спектральных коэффициентов отражения, предложенный в [6] и [8], соответственно. Для того, чтобы определить неизвестное распределение тока, представим интеграл в виде многочлена:
![]()
![]() ,
, ![]() ,
, ![]() , (3)
, (3)
где Imk - неизвестные текущие коэффициенты, Mk - степень многочлена. Неизвестные текущие коэффициенты будут определяться решением системы интегральных уравнений Галена. Эта система удовлетворяет граничным условиям для тангенциальной составляющей электрического поля на поверхности антенны. Затем будет сформирована соответствующая система линейных уравнений с использованием метода сопоставления в точке. Решение полученной системы уравнений, позволит определить неизвестное распределение тока вдоль провода антенны, и на его основе, входное сопротивление ГДА в воздухе над границей раздела сред:
![]() . (4)
. (4)
Результаты расчётов
Результаты анализа полуволновой ГДА, размещённой в воздухе слева от границы раздела сред (![]() ), приведены на рис. 2. Значения входного импеданса соответствуют случаю симметричной ГДА с радиусом поперечного сечения
), приведены на рис. 2. Значения входного импеданса соответствуют случаю симметричной ГДА с радиусом поперечного сечения ![]() . В ходе вычисления распределения тока был использован полином второго порядка. Результаты представлены как функции нормированной удельной проводимости в нижней половине пространства для трех значений относительной диэлектрической проницаемости er1= 1.001, 2.1, и 9. Соответствующие значения из [2], полученные с помощью выражения для третьего порядка распределения тока, показаны на том же графике. В работе [2] автор также применил метод соответствия в точке для решения интегральных уравнений Галена в сочетании с полиномиальным распределением тока. Однако, интегралы Зоммерфельда были решены по-разному с использованием высокоточного численного метода, предложенного в [5].
. В ходе вычисления распределения тока был использован полином второго порядка. Результаты представлены как функции нормированной удельной проводимости в нижней половине пространства для трех значений относительной диэлектрической проницаемости er1= 1.001, 2.1, и 9. Соответствующие значения из [2], полученные с помощью выражения для третьего порядка распределения тока, показаны на том же графике. В работе [2] автор также применил метод соответствия в точке для решения интегральных уравнений Галена в сочетании с полиномиальным распределением тока. Однако, интегралы Зоммерфельда были решены по-разному с использованием высокоточного численного метода, предложенного в [5].
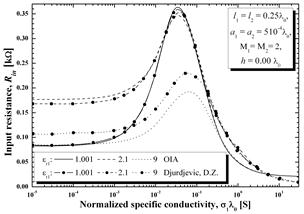
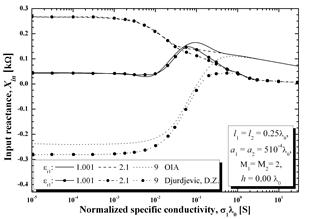
Рисунок - 2. Входное сопротивление (активное и реактивное) полуволнового диполя ГДА и сравнение с нормированной проводимостью полупространства с потерями,![]()
Рис. 3а, и 3б иллюстрируют нормированные распределения тока для ГДА, длиной равной длине волны. Две цифры соответствуют двум различным значениям относительной диэлектрической проницаемости er1= 2.1 и 5. В результате применения указанных методов и моделей, были получены результаты, представленные сплошной кривой, в то время как пунктирная линия соответствует результатам, взятым из [2]. Учитывая тот факт, что это был случай, когда длина ГДА была равна длине волны, порядок полинома текущего приближения должен быть выше, чем в случае ранее проанализированного полуволнового диполя. Для получения результатов, приведенных на обоих рисунках, использован полином следующих порядков: М1 = М2 = 2,3 и 4. Отсюда можно сделать вывод о том, что полинома четвертого порядка было уже достаточно, чтобы достичь желаемого уровня точности расчётов.
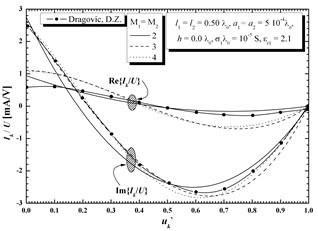
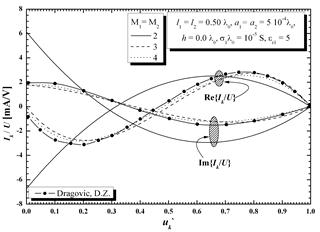
Рисунок 3 - Реальная и мнимая составляющие нормированного распределения тока вдоль ГДА длиной, равной длине волны для двух значений диэлектрической проницаемости.
На рис. 4 и 5 показаны полученные результаты для входного сопротивления (реальной и мнимой составляющих) для ГДА той же самой длины для двух значений электрической проницаемости (er1= 2.1 на рис. 4, er1= 5 на рис. 5). Опять же, из-за длины антенны, порядок многочлена был увеличен, и результаты, показанные на рисунках, соответствуют значениям: М1 = М2 = 3, 4, 5 и 6. Кроме того, как и для полуволнового диполя, для сравнения приведены результаты из работы [2], которые были получены с помощью полинома четвертого порядка. Хорошее соответствие двух наборов результатов достигается при многочлене порядка пяти.
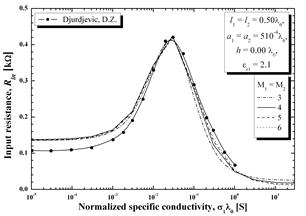
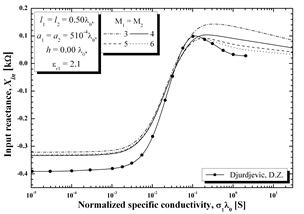
Рисунок 4 - Входное активное и реактивное сопротивление для ГДА с длиной, равной длине волны в зависимости от нормированной проводимости для полупространства с потерями с диэлектрической проницаемостью er1= 2.1, h/l0 = 0.
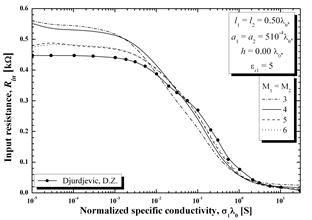
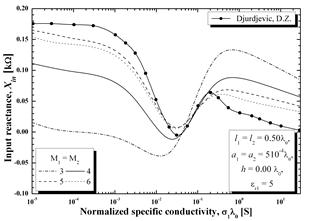
Рисунок 5 - Входное сопротивление (активное и реактивное) для ГДА с длиной, равной длине волны в зависимости от нормированной проводимости для полупространства с потерями с диэлектрической проницаемостью er1= 5, h/l0 = 0.
Заключение
На основе проведенного анализа и представленных результатов, можно сделать вывод, что относительно сложная проблема анализа антенн, расположенных на границе раздела между воздушной средой и средой с потерями может быть решена достаточно точно с помощью описанного метода. Это указывает на возможность применения описанной методики расчёта для точной оценки электрических параметров антенны (или обнаружения изменений в параметрах), основываясь на известной величине входного импеданса / адмиттанса антенны. Анализ проведённых в этой статье расчётов показывает, что близость расположения антенны к однородной изотропной среде не представляет проблемы, т.е. не уменьшает точность вычислений.
Данную методику расчёта можно использовать при расчёте СВЧ антенн с магнитоэлектрическим заполнением и в дальнейшем применить для расчёта сложных СВЧ устройств.
Работа, представленная в статье, выполнена в рамках реализации проекта TR 33008 поддержанного Министерством образования и науки Сербии и в рамках реализации Федеральной Целевой Программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.
Рецензенты:
Захаров Анатолий Юльевич, д.ф.-м.н., профессор, заведующий секцией кафедры общей и экспериментальной физики Института электронных и информационных систем НовГУ, г.Великий Новгород.
Корнышев Николай Петрович, д.т.н., доцент, ведущий научный сотрудник НИИ ПТ «РАСТР», г.Великий Новгород.



