В рамках информационно измерительной системы доля радиотехнических задач, связанных с прохождением аналогового сигнала от датчика до измерителя, заметно снизилась с внедрением принципов децентрализации первичной обработки. В случае предельно близкого расположения АЦП у источника сигнала отпадает необходимость в учете мультипликативных составляющих помехи и шумов, которые всегда были как результат нежелательного изменения параметров звеньев системы. При этом возрастает влияние аддитивной составляющей на форму сигнала. Характер этой составляющей требует детального анализа в связи с кардинальным изменением сигнальной обстановки при постоянном росте требований к точности измерений.
Подавляющее преимущество цифровой электроники во многом определяет характер шумовой составляющей в первичных аналоговых сигналах. Потоки цифровых данных, служебной информации, результатов обработки, управляющих воздействий в основном концентрируются в единой среде обмена сигналами - шине. Многопроцессорные вычислительные ресурсы свидетельствуют о преимуществах территориального распределения процедур цифровой обработки с сочетаниями параллельных и последовательных способов обработки, дуплексных и полудуплексных режимов обмена данными в физических и радиочастотных цифровых каналах связи.
Поэтому генераторами шумовой составляющей в выходном сигнале датчика являются импульсные сигналы. Шум от множества импульсов можно представлять в виде случайного процесса, образованного флуктуациями мгновенного значения относительно среднего значения амплитуды импульса. Временной и спектральный анализ цифрового шума показали, что это - дельта-коррелированный вероятностный процесс с равномерным энергетическим спектром.
В статье синтезируется алгоритм шумоподавления в рамках теории приближения при оценке близости аппроксимирующей и аппроксимируемой функции с использованием критерия равномерного приближения или максимальной ошибки. По мнению автора, при таком подходе задача подавления шума, распределенного и в области спектра сигнала, может быть решена для условий реального масштаба времени.
В основе синтеза нового алгоритма лежат следующие утверждения.
- 1. Математическая теория аппроксимации и интерполяции функций не предполагает в качестве обязательного условия равномерность отсчетов. [1]
- 2. Для аппроксимации без скачков производных необходимо использовать куски функций с переменной кривизной, располагая их между смежными отрезками кусочно-многочленных функций с разнородной структурой, составленных из многочленов разной степени. [2]
- 3. Для гладкого сопряжения кусков аппроксимации узлы должны выбираться на участках сигнала с минимальными значениями первой и второй производной.
Критерий равномерного приближения необходим для решения задач в реальном масштабе времени, но его недостаточно для задачи шумоподавления. Вторым критерием оптимизации должен стать критерий равномерного распределения погрешности аппроксимации на участке сигнала. Этот критерий также необходим и в то же время, он и достаточен для оптимального сглаживания сигнала, т.е. шумоподавления.
Метод подавления аддитивных помех рассматривается как адаптированный к сигналу отбор существенных отсчетов, по которым возможен следующий процесс восстановления сигнала:
- - восстановление формы сигнала с использованием полинома нулевой степени для постоянного участка (усреднение).
- - восстановление формы сигнала с использованием полинома первой степени для линейного участка (линеаризация);
- - восстановление формы сигнала с использованием полинома второй степени для нелинейного участка (аппроксимация).
За основу предлагается взять апертурный алгоритм адаптивной дискретизации нулевого порядка (НП), получивший широкое распространение за счет предельной простоты и имеющий высокую эффективность при обработке сигналов с низкой динамичностью. Неравенство, при выполнении которого отсчет сигнала в момент времени tj признается существенным, записывается следующим образом:
![]() ,
,
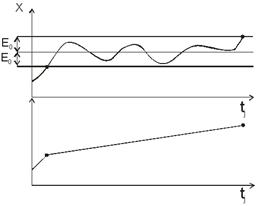
где Е0 - величина апертуры, составляющая десятки процентов от динамического диапазона сигнала. Участок сигнала между существенными отсчетами tj-1 и tj при восстановлении аппроксимируется линией и составляющие шума в пределах Е0 таким образом подавляются (рис. 1).
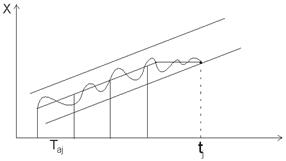
Свойство подавления шума для алгоритма нулевого порядка теряется на наклонных и нелинейных участках сигнала. Синтезируя дополнительные условия, которые бы следили за уклонением сигнала от аппроксимирующей наклонной прямой, можно распространить эффект шумоподавления и на участки сигнала, где есть первая производная (рис. 2).
|
|
|
|
Рис. 1. Подавление шума алгоритмом НП |
Рис. 2. Слежение за сигналом на линейном участке |
Сформированные алгоритмом НП отрезки времени tj - tj-1 называются адаптивными интервалами Taj в терминах нерегулярной дискретизации. Эти интервалы содержат информацию о первой производной в сигнале (косвенно, как Е0/Та). На линейных участках сигнала адаптивные интервалы должны быть равны между собой. Устанавливая допуск на неравенство интервалов Taj, тем самым устанавливается допуск на линейность участка. Если решение о существенности отсчета принимается путем поочередного сравнения одного из адаптивных интервалов (назовем его базовым Тб, сформированный алгоритмом НП) с последующими интервалами, то получим апертурный алгоритм первого порядка (ПП). Определим интегральный допуск на разности указанных интервалов следующими условиями:
![]() , (1)
, (1)
![]() . (2)
. (2)
Иными словами, участок сигнала можно считать линейным, пока модуль суммы разностей Taj и Tб не превысит kTб, где k задает величину апертуры на линейном участке и лежит в пределах от 0,1 до 1,5. Определение величины k возможно на этапе схемной реализации алгоритма с учетом критерия равномерного распределения ошибок аппроксимации.
Система неравенств подчеркивает тот факт, что существенные отсчеты НП (1) исключаются из потока по условию (2). Величина kТб выбрана в качестве ограничения условия (2) по соображениям равенства величины допустимого уклонения сигнала от аппроксимирующей прямой для НП и ПП.
Дополняя предложенную систему неравенств новыми условиями учета нелинейности, получаем алгоритм второго порядка (ВП), как следующую дополнительную ступень. Обработку нелинейного участка предлагается вести по двум направлениям в зависимости от знака первой производной в сигнале.
При смене знака первой производной в сигнале отсчет tj признается существенным и вместе с базовыми отсчетами НП составляет опорную выборку для проведения через них параболической кривой. Неравенства (1), (2) дополняются контролем знака производной в сигнале:
![]() (3)
(3)
Выполнение неравенства (3) свидетельствует о нелинейности участка сигнала. При этом новый базовый интервал не измеряется и продолжается слежение за линейностью сигнала.
В случае заметного увеличения первой производной в сигнале предлагается вести слежение за смежными адаптивными интервалами Та. На крутых участках составляющие шума сливаются с сигналом и величина допуска на уклонение сигнала от аппроксимирующей кривой может быть уменьшена без снижения эффекта шумоподавления при снижении ошибки аппроксимации. Система условий для алгоритма ВП в этом случае может быть представлена неравенством (1) совместно с
![]() . (4)
. (4)
С учетом утверждения 2, в начале участка, где первая и вторая производные равны нулю, алгоритм ПП или ВП дополнительно без выполнения неравенства (1) должен формировать существенный отсчет. Условие определения такого участка для ступени ПП:
![]() ,
,
для ступени ВП:
![]() .
.
При восстановлении сигнала по существенным отсчетам интерполяционным полиномом второй степени составляющие шума в пределах 2Е0 подавляются.
СПИСОК ЛИТЕРАТУРЫ:
- 1. Лоран П.Ж. Аппроксимация и интерполяция. М.: Мир, 1975. 221 с.
- 2. Победоносцев В.А. Основания информметрии. - М.: Радио и связь, 2000. 192 с.