Возникновение нестационарности течений воды в реках и каналах связано с катастрофическими осадками или сбросами значительных объемов воды из водохранилищ. Из данных наблюдений следует, резкое увеличение стока нередко сопровождается обострением переднего фронта течения и внезапным резким увеличением уровня реки на большом расстоянии от водохранилищ и зон осадков. Особенно это явление заметно при выполаживании течения, на равнинной части реки, где, казалось бы, следовало ожидать спокойного медленного повышения уровня.
При нестационарном стоке при пологом возрастающем начальном переднем фронте течения со временем происходит его обострение. В конечном итоге фронт течения становится ударным прямоугольным. Это утверждение полностью соответствует многим данным наблюдений. Появление ударного фронта течения часто сопровождается разрушением мостов и прибрежных построек. Поэтому необходимо предложить эффективные способы, препятствующие его появлению.
При импульсном сбросе жидкости из резервуара возможно появление локальных процессов, по форме похожих на длинные волны малой амплитуды, распространяющиеся на значительные расстояния от места сброса вдоль течения. Как известно [2], в идеальной жидкости эти волны имеют сильно выраженную локальную структуру и форму так называемых солитонов или уединенных волн Кортевега – де Фриза (КдФ)[4] (рис. 1б).
Рис. 1а. Начальное положение жидкости в канале
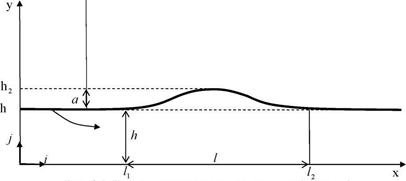
Рис. 1б. Длинная волна малой амплитуды (солитон)
Рассмотрим находящуюся выше уровня канала в резервуаре жидкость (рис. 1а). Когда перегородка l0, отделяющая жидкость от канала, внезапно отодвигается и затем через некоторый промежуток времени снова задвигается, происходит небольшой сброс и возникает длинная колоколообразная волна, движущаяся вдоль канала (рис. 1б). При этом если не появляется рябь, в которой волна рассеивается по всей поверхности [1], возникает импульс в виде устойчиво распространяющейся волны, которая перемещается по жидкости, оставляя ее за собой в неподвижном состоянии.
В реальных ситуациях, при сбросе небольших объемов жидкости, условия, при которых образуется единичный солитон, очень идеализированы и соответствуют начальным условиям опытов Хаммака и Сигура, Вейдмана и Максуори, обобщенные результаты которых приведены в [4]. Например, в бассейне длиной 31,6 м, глубиной 61 см и шириной 39,4 см, при начальной длине l0 = 61 см и высоте h1 - h = 40 см сброса, возникает солитон длиной l2 -l1 = 87 см и высотой h2 - h = 31 [4]. Там же показано, что при увеличении сброса возникают ситуации, при которых появляется несколько солитонов. Хотя в [5] получено n-солитонное решение уравнения КдФ, до конца процессы взаимодействия, а, следовательно, вопросы распространения группы солитонов остаются не изучены, так как математический аппарат разработан недостаточно, известно, что скорость распространения солитона зависит от его амплитуды [6], однако, из всей этой группы наибольший интерес представляет самый большой солитон, а значит, и самый быстрый. Действительно, через какой-то промежуток времени большой солитон обгонит все маленькие, и на расстоянии от места сброса его можно рассматривать как единичный и пользоваться полученными результатами.
Предполагается, что на поверхности жидкости существует длинная волна малой амплитуды, то есть максимальная амплитуда возмущения а мала по сравнению с глубиной h канала, а длина возмущения l велика по сравнению с h .
Движение жидкости описывается вектором скорости V(x, у, t) = iu (x, у, t) + jv( x, у, t), где i и j – единичные векторы горизонтального и вертикального направлений соответственно. Пусть движение жидкости безвихревое, так что 
. Предполагается также, что плотность жидкости 
постоянна, так что уравнение неразрывности 
сводится к уравнению . Тогда следует, что 
и 
.
Снизу жидкость ограничена твердым горизонтальным дном, имеющим форму 
. Верхней границей является свободная поверхность 
. Все вычисляемые на этой поверхности члены будут обозначены индексом 1. Для свободной поверхности 
запишем:
Так как,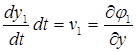
и 
получено первое граничное
условие на поверхности жидкости в одной из следующих форм:
.
Из соотношения импульсов, запишем уравнение Эйлера [5]
,
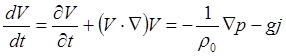где 
– постоянная плотность жидкости, p – давление в произвольной точке жидкости и g – ускорение силы тяжести, учитывая, что движение жидкости безвихревое, записывается второе граничное условие на поверхности жидкости:
.
Таким образом, движение поверхности жидкости описывается решением уравнения Лапласа, удовлетворяющего последним двум нелинейным граничным условиям.
Как показано в [7], уравнением, описывающим распространение длинных волн малой амплитуды, является уравнение Кортевега – де Фриза. Процедура вывода КдФ, опирающаяся на ранее рассмотренные условия, приведена в [5]. В безразмерных координатах уравнение КдФ имеет вид:
,
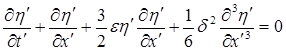здесь независимые переменные 
и 
, зависимые
, 
и 
- малые параметры разложения в ряд компонент скорости 
, 
. Преобразованием 
исключаем член 
. Полученное уравнение принимает вид классического уравнения Кортевега – де Фриза, если умножить его на 
и затем величину 
положить равной q:
,
где 
.
В размерных переменных уравнение КдФ имеет вид:
.
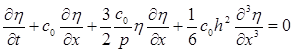Таким образом, форма длинной волны малой амплитуды 
, распространяющейся в идеальной жидкости в момент времени t , подчиняется уравнению Кортевега – де Фриза:
,
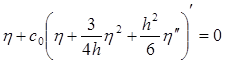где точкой обозначена производная по времени, а штрихом – производная по координате. Здесь профиль волны 
определяет наклон касательной к графику в точке x в момент t, а – скорость движения точки графика по направлению оси . Этот профиль смещается и деформируется с течением времени.
КдФ-уравнение описывает волны, распространяющиеся в одном направлении вдоль оси х. Эффекты дисперсии определяются членом ~
, а нелинейные эффекты – членом ~
. Если ими пренебречь, то из уравнения КдФ получится уравнение:
.
Общее решение этого уравнения – это любая функция от 
, то есть 
[19]. Чтобы найти зависимость п от x в любой момент времени, достаточно нарисовать график функции 
и двигать его со скоростью c0 (c0 > 0) в положительном направлении оси x. Волне, бегущей в противоположном направлении, соответствует другой знак перед c0.
Как известно [7], волновое уравнение Даламбера описывает волны, бегущие в обоих направлениях. Тогда как КдФ-уравнение не обладает этим свойством, в то время как волны на поверхности жидкости от переданного ей импульса бегут в обоих направлениях. Если нас не интересует начальный момент, то мы можем отдельно изучать одну и другую волну.
Если эффекты нелинейности и дисперсии достаточно малы, то обе волны убегут на большое расстояние друг от друга за столь малое время, что эти эффекты не успеют сказаться, и в дальнейшем можно следить за эволюцией одной из волн, забыв о существовании другой. Именно поэтому можно описывать эволюцию обеих волн одинаковым по виду уравнением с разными знаками перед с0 [7].
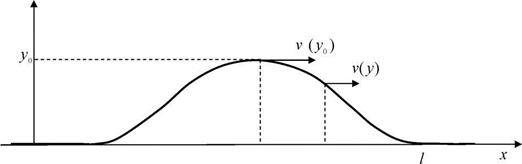
Рис. 2а. Уединенная волна, входящая в область с сильной нелинейностью
Рассмотрим процесс эволюции уединенной волны. Пусть в уравнении КдФ нелинейный член значительно превосходит член, определяющий дисперсию 
. Тогда последним членом можно пренебречь и рассматривать уравнение вида 
. Пусть на поверхности воды образовалась уединенная волна (рис. 2а). Дальнейшая судьба этой волны, при условии равенства нулю дисперсии, определяется тем, что скорость каждой точки графика зависит от ее высоты. Как известно из [7], для волн КдФ эта зависимость простейшая:
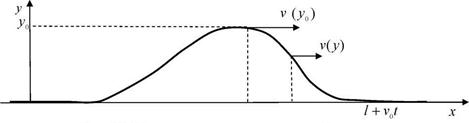
Рис.2б. Уединенная волна, в некоторый момент времени t
.
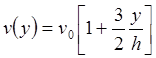Быстрее всех движется вершина горбика. Ее скорость равна:
,
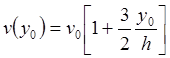а скорость переднего фронта волны, где у = 0, равна v0. Поэтому в некоторый следующий момент времени передняя часть волны станет более крутой (рис. 2б), а с течением времени произойдет «опрокидывание» волны (рис. 2в).
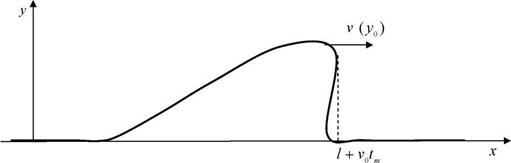
Рис. 2в. Опрокидывание уединенной волны, в момент времени tm
Таким образом, установлено, что при небольших выбросах воды из водохранилищ возможно появление уединенных волн (солитонов), распространяющихся на большие расстояния вдоль течения каналов. Точное описание указанных волн дает уравнение Кортевега – де Фриза. При этом уединенные волны со временем могут не только расплываться при наличии сильной дисперсии, но и обостряться на своем переднем фронте при сильной нелинейности.
Рецензенты:
Магомедова А. В., д.т.н., профессор, Дагестанский государственный технический университет, г. Махачкала.
Назаралиев М. А., д.ф.-м.н., профессор, Дагестанский государственный университет, г. Махачкала.