Введение
Усложнение современных объектов исследований, повышение требований к точности и быстродействию измерений, рост числа и диапазонов измеряемых параметров, приводит к необходимости создания новых способов измерений и совершенствования современных средств измерения, преобразования информации. Развитие информационно-измерительных систем, предназначенных для обеспечения высоких метрологических и эксплуатационных характеристик, требует использования элементов и устройств вычислительной техники, обеспечивающих возможность вычислений в процессе преобразования [4].
Создание современных цифровых информационно-измерительных систем параметров гармонических сигналов
В многообразии существующих сигналов циркулирующих в современных элементах и устройствах вычислительной техники и систем управления широко распространены гармонические сигналы. Существует большое разнообразие способов измерения параметров гармонических сигналов базирующихся на методах цифровой обработки сигналов с применением преобразования Фурье, на основе мгновенных отсчетов, на базе метода синхронного детектирования, интегральных выборок и т.д. Основными недостатками информационно-измерительных систем и входящих в них измерительных преобразователей, реализуемых на этих методах, являются: значительные временные задержки на получение выборок; формирование интегральной оценки измеряемых параметров, необходимость использования эталонных сигналов и др.
Отсюда одной из актуальных проблем является создание современных цифровых информационно-измерительных систем параметров гармонических сигналов, использующих новые эффективные алгоритмы, способы и структуры, ориентированные на применение вычислительных операций и механизмов адаптации [4].
Учитывая современные тенденции, связанные с минимизацией аппаратурных затрат, увеличением быстродействия, оптимизацией метрологических характеристик за счет реализации механизмов адаптации, в рамках исследований была поставлена задача апробации и построения модели информационно-измерительной системы реализующей новый способ измерения параметров гармонического сигнала удовлетворяющего всем необходимым метрологическим характеристикам при этом без реализации механизма синхронизации, с временем измерения не превышающим половины периода сигнала и возможностью применения механизмов адаптации к изменяющимся параметрам сигнала описанного в [4].
Согласно исходной постановки задачи и условий определено, что входной гармонический сигнал измерительного преобразователя в общем случае имеет вид:
![]() . (1)
. (1)
Уравнение (1) содержит три неизвестных величины: амплитуду Ux, частоту fx и текущую начальную фазу сигнала ![]() . При этом Ux, fx являются измеряемыми параметрами (характеризуют сигнал), а
. При этом Ux, fx являются измеряемыми параметрами (характеризуют сигнал), а ![]() – сопутствующим расчетным (обозначим индексом – *) параметром, который характеризует насколько гармонический сигнал отклонен от точки соответствующей моменту начала измерения (запуска линейно изменяющихся сигналов), данную величину будем называть именно текущей начальной фазой, так как моменты начала измерений могут быть произвольными, то и соответственно значения текущей начальной фазы будут численно меняться в разные моменты времени. Необходимость расчета значения
– сопутствующим расчетным (обозначим индексом – *) параметром, который характеризует насколько гармонический сигнал отклонен от точки соответствующей моменту начала измерения (запуска линейно изменяющихся сигналов), данную величину будем называть именно текущей начальной фазой, так как моменты начала измерений могут быть произвольными, то и соответственно значения текущей начальной фазы будут численно меняться в разные моменты времени. Необходимость расчета значения ![]() состоит в том, что данная величина, в процессе измерения, позволит компенсировать погрешность синхронизации гармонического и уравновешивающих сигналов, а также реализовать механизмы адаптации, но для этого нам необходимо получение трех отсчетов (использование тройного развертывающего преобразования), при этом значение фазы может меняться в некотором диапазоне
состоит в том, что данная величина, в процессе измерения, позволит компенсировать погрешность синхронизации гармонического и уравновешивающих сигналов, а также реализовать механизмы адаптации, но для этого нам необходимо получение трех отсчетов (использование тройного развертывающего преобразования), при этом значение фазы может меняться в некотором диапазоне ![]() .
.
Учитывая вид сигнала (1) и то, что сигнал имеет три неизвестных параметра общую постановку задачи, в рамках рассматриваемой информационно измерительной системы базовую задачу по определению значений параметров можно свести к необходимости решения системы уравнений с тремя неизвестными вида (2)
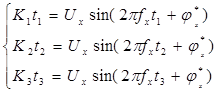 , (2)
, (2)
где К1, К2, К3 – значения коэффициентов пропорциональности уравновешивающего линейно изменяющегося сигнала; t1, t2, t3 – значения временных отсчетов. Графически представление параметров и значений данной системы уравнений может быть показано в виде, представленном на рисунке 1.
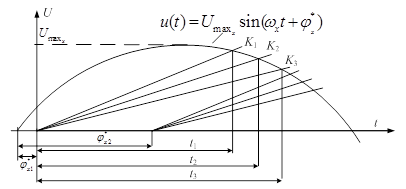
Рис. 1. Временное представление сигнала при использовании тройного
развертывающего преобразования на основе зависимых временных отсчетов
При проведении научных исследований в рамках реализации федеральной целевой программы «Научные и научно педагогические кадры инновационной России» на базе СПбГТЭУ «ЛЭТИ» по исполнению ГК № 14.B37.21.0180 были предложены новые подходы по построению адаптивных информационно-измерительных систем параметров гармонических сигналов. Ключевые результаты были получены на основе построенной модели адаптивной информационно-измерительные системы параметров гармонических сигналов.
В рамках проводимых исследований был осуществлен обзор отечественных и зарубежных достижений в области информационно-измерительные системы параметров гармонических сигналов. На основе подходов предложенных в [1-2] была осуществлена разработка адаптивной информационно-измерительной системы на базе адаптивного цифрового измерительного преобразователя параметров гармонических сигналов на основе тройного развертывающего преобразования предложенного в [4].
Полученные путем теоретических изысканий решения и структуры перед практической реализацией требуют тщательного анализа и проверки. Одним из эффективных способов оценки и анализа результатов является построение и исследование модели на основе полученных данных, при этом необходимо заметить, что разработка системы не может быть признана адекватной без соответствующего построения модели системы. На разных этапах разработки систем могут использоваться различные типы моделей.
Так на базе [1 - 3] были построены соответствующие аналитические модели, а на основе подходов предложенных в [1, 2, 4] были построены имитационные модели в среде MatLab. На рисунке 2 представлена обобщенная схема модели.
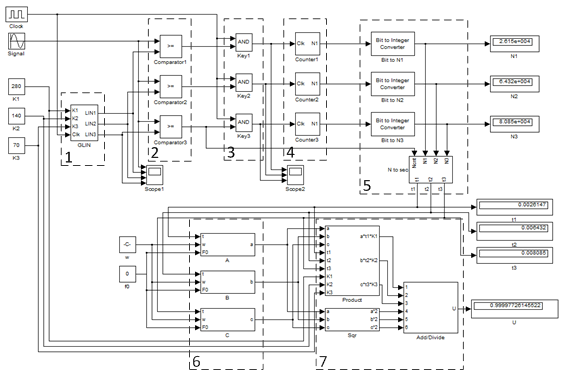
Рис. 2. Обобщенная схема модели
Модель измерителя можно условно разделить на 7 функциональных логических блоков: блок 1 представляет собой схему генерации линейно изменяющегося напряжения, 2 – компараторы, 3 – ключи, 4 –цифровые последовательные счетчики импульсов выполненные на D-триггерах, 5 – блок преобразования значений числа импульсов в различные форматы, 6 – блок разложение функции sin, 7 – блок расчета амплитуды сигнала.
На входе системы находятся тактовый генератор, источник гармонического сигнала и источники сигналов с постоянными значениями напряжения К1, К2, К3.
В блоке 1 сигналы с постоянными значениями напряжения К1, К2, К3 преобразуются в линейно изменяющиеся сигналы согласно соотношения (3):
![]() (3)
(3)
Линейно изменяющиеся сигналы поступают на блок 2, где с помощью компараторов мгновенные значения их напряжений ![]() сравниваются с мгновенным значением напряжения
сравниваются с мгновенным значением напряжения ![]() искомого гармонического сигнала. В случае если
искомого гармонического сигнала. В случае если ![]() – на выходе компаратора установлена логическая “1”, при выполнении условия
– на выходе компаратора установлена логическая “1”, при выполнении условия ![]() – на выходе компаратора устанавливается логический “0”. Сигналы на выходе компаратора открывают и закрывают ключи в блоке 3, через которые к счетчикам проходят импульсы от тактового генератора. Таким образом, в момент начала работы схемы, ключи находятся в открытом положении и счетчики в блоке 4 начинают подсчет импульсов, поступающих от тактового генератора.
– на выходе компаратора устанавливается логический “0”. Сигналы на выходе компаратора открывают и закрывают ключи в блоке 3, через которые к счетчикам проходят импульсы от тактового генератора. Таким образом, в момент начала работы схемы, ключи находятся в открытом положении и счетчики в блоке 4 начинают подсчет импульсов, поступающих от тактового генератора.
В момент равенства входного напряжения и напряжения на первом выходе генератора линейно изменяющегося напряжения срабатывает первый компаратор. Сигнал компаратора закрывает соответствующий ключ, в первом счетчике записывается число импульсов N1. В момент равенства входного напряжения и напряжения на втором выходе генератора линейно изменяющегося напряжения срабатывает второй компаратор – во втором счетчике фиксируется число N2. Аналогично, в момент равенства входного напряжения и напряжения на третьем выходе генератора линейно изменяющегося напряжения, в третьем счетчике фиксируется некоторое число N3.
В блоке 5 значения числа импульсов с выходов счетчиков преобразуются из двоичного формата в десятичный. Десятичные значения числа импульсов отображаются на индикаторах N1, N2, N3. Далее значения числа импульсов преобразуются во временные отчеты t1, t2, t3 по формуле (4):
![]() (4)
(4)
где Т – период следования тактовых импульсов.
Временные отчеты t1, t2, t3 отображаются на соответствующих индикаторах. t1 – момент равенства входного напряжения и напряжения на первом выходе генератора линейно изменяющегося напряжения, t2 – момент равенства входного напряжения и напряжения на втором выходе генератора линейно изменяющегося напряжения, t3 – момент равенства входного напряжения и напряжения на третьем выходе генератора линейно изменяющегося напряжения.
Временные отчеты поступают на вход блока 6, на вход которого также подаются значения частоты и начальной фазы сигнала. В блоке 6 происходит формирование рядов вида:
![]()
Величина m влияет на точность измерений и для данной модели имеет фиксированное значение равное 7.
В блоке 7 осуществляется суммирование, умножение и деление полученных выражений, в результате чего получаем на выходе блока 7 вычислительного устройства расчетное значение амплитуды:
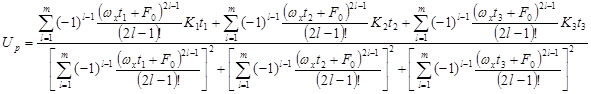
Расчетное значение применительно для данного примера – амплитуды отображается на индикаторе U.
На рисунке 3 показана временная диаграмма работы модели измерителя амплитуды гармонических сигналов.
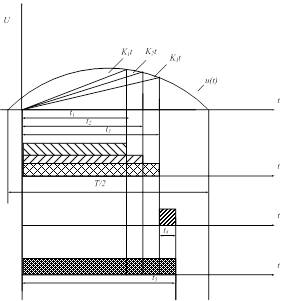
Рис. 3. Временная диаграмма работы модели
На ней представлена работа измерителя амплитуды гармонических сигналов для временного промежутка равного половине периода сигнала. В течение временного интервала t3 формируются значения временных отсчетов, значения которых используются в дальнейших вычислениях. За промежуток t4 происходит расчет амплитуды сигнала. Весь процесс вычислений занимает промежуток времени t5 (время измерения амплитуды укладывается в промежуток времени в пределах половины периода синусоидального сигнала, если значения частоты не превышают 3000 Гц, для более высоких частот анализ в данной работе не производился).
Заключение
В процессе исследований были спроектированы и смоделированы адаптивные измерители параметров гармонических сигналов возможные к использованию и эксплуатации как средство диагностики и анализа.
В рамках построенных моделей была произведена адаптивная оценка критериев при измерении и анализе состояния параметров информационных систем.
В рамках проводимых экспериментальных исследований на макетах в учебно-научных лабораториях СПбГЭТУ были получены результаты подтверждающие адекватность разработанной структуры и близки к значениям, полученным в результате аналитических расчетов на основе [1]. Примеры полученных значений представлены в Таблице 1.
Таблица 1 – Результаты аналитического и имитационного моделирования
|
|
|
Ux (аналит.), В |
Ux (имитац.), В |
eU (аналит.), % |
eU (имитац.), % |
fx (аналит.), Гц |
fx (имитац.), Гц |
e f (аналит.), % |
e f (имитац.), % |
|
1 |
50 |
0,99998 |
0,99997 |
0,002 |
0,003 |
50,0012 |
50,0014 |
0,002 |
0,003 |
|
5 |
50 |
4,99988 |
4,99985 |
0,002 |
0,003 |
49,9989 |
49,9984 |
0,002 |
0,003 |
|
10 |
50 |
9,99976 |
9,99972 |
0,002 |
0,003 |
49,9988 |
49,9982 |
0,002 |
0,004 |
|
1 |
150 |
0,99997 |
0,99997 |
0,003 |
0,003 |
150,0039 |
150,0045 |
0,003 |
0,003 |
|
5 |
150 |
4,99988 |
4,99985 |
0,003 |
0,003 |
150,0042 |
149,9942 |
0,003 |
0,004 |
|
10 |
150 |
9,99976 |
9,99956 |
0,003 |
0,004 |
149,9953 |
150,0063 |
0,003 |
0,004 |
|
1 |
500 |
0,99996 |
0,99995 |
0,004 |
0,005 |
500,0192 |
500,0216 |
0,004 |
0,004 |
|
5 |
500 |
4,99978 |
4,99973 |
0,004 |
0,005 |
499,9811 |
499,9751 |
0,004 |
0,005 |
|
10 |
500 |
9,99957 |
9,99947 |
0,004 |
0,005 |
500,0184 |
500,0234 |
0,004 |
0,005 |
Рецензенты:
Новиков Владислав Александрович д.т.н., профессор кафедры РАПС Санкт-Петербургского государственного электротехнического университета, г.Санкт-Петербург.
Поляхов Николай Дмитриевич д.т.н., профессор кафедры САУ Санкт-Петербургского государственного электротехнического университета, г.Санкт-Петербург.



