В последние десятилетия широкое развитие в промышленности получили газодинамические методы формирования защитных покрытий на поверхностях конструкций. Физический принцип этих методов базируется на использовании гетерогенных струй с широким диапазоном изменения скоростей и температур [3, 4, 5].
Газодинамические методы сыграли определяющую роль в разработке принципиально новых, наукоемких технологий синтеза разнофункциональных покрытий. Например, плазменная технология впервые решила задачу создания материалов с новыми свойствами (интерметаллиды, металлокерамики и др.). Однако при всей простоте и мобильности этих методов, они обладают рядом существенных недостатков, связанных, прежде всего, с использованием высокотемпературных (несколько тысяч градусов) газовых струй высокой химической активности. Такие свойства газа-носителя оказывает в технологическом процессе необратимые отрицательные действия. Например, изменяются размеры частиц вследствие испарения. Нарушается компонентный состав исходного материала порошка (химическое реагирование частиц с высокотемпературным газом-носителем). Все это ухудшает свойства создаваемого покрытия и исключает достижения желаемого качества.
Понятно, что исключение этих недостатков из технологического процесса возможно только в случае устранения фазовых переходов (снижение температуры струй), а также блокирование в газе-носителе гомогенных и гетерогенных химических реакций. Это может быть достигнуто только двумя способами, либо использованием инертных газов в качестве носителей частиц, либо существенным снижением температуры газовой фазы до 500... 600К. Последний способ неприемлем для традиционных плазменных, газопламенных и электродуговых методов.
Впервые устранение этих недостатков было реализовано в Институте теоретической и прикладной механики СО АН СССР, сотрудники которого для формирования покрытий разработали холодный газодинамический метод (ХГМ), (без подогрева газа-носителя, А.С. №1618778)
Практически в этот же период в Московском авиационном институте (государственном техническом университете) разработан и получил приоритет низкотемпературный газодинамический метод (НТГДМ) [1,6]. В методе, с целью оптимизации процессов формирования покрытий, газ-носитель (технический воздух) предварительно нагревался на несколько десятков или сотен градусов. В дальнейшем предложенный метод нанесения покрытий получил наименование НТГДМТ - технологии.
1. Сущность низкотемпературного газодинамического метода формирования покрытий
Сущность НТГДМТ - технологии заключается в том, что покрытия наносятся в результате соударения высокоскоростных (М > 1) гетерогенных потоков с подложкой. Для получения нужных свойств покрытия, его компонентный состав "набирается" из необходимого количества химических элементов или соединений химических элементов (металлов, оксидов, карбидов и др.) в виде композиции порошков. Дисперсность частиц в таких порошках в зависимости от плотности компонентов может меняться от 2 до 20 мкм. Оптимальным является применение в составе композиций нанопорошков. Полученная композиция порошков, составленная в соответствующих массовых долях, предварительно перемешивается с незначительно подогретым газом-носителем в специальном смесителе, а затем разгоняется в сверхзвуковом сопле до расчетной для каждой композиции скорости. Организация такого технологического процесса обеспечивает частицам высокую кинетическую энергию, значительная доля которой при соударении с подложкой переходит в тепловую. Эта теплота в сочетании с высокими уровнями напорного давления создают в процессе удара высокие адгезионные и когезионные свойства покрытий и, практически, физическую плотность материала покрытия (пористость покрытия не превышает 1,5%).
Одним из важнейших преимуществ НТГДМ по сравнению с другими газотермическими методами является то, что покрытие формируется за счет высокого уровня кинетической энергии частиц, в то время как температура гетерогенного потока остается значительно меньше температуры плавления материала частиц. Низкий уровень температуры исключает физико-химические превращения в гетерогенном потоке, поэтому частицы достигают подложки в своем исходном состоянии. Это позволяет использовать в качестве газа-носителя в ряде случаев дешевый технический воздух.
2. Математическая модель течения гетерогенной смеси при наличии межфазного теплообмена
При формировании защитных покрытий газодинамическими методами, например, с применением, НТГДМ - технологии, высокое качество покрытий обеспечивается скоростью частиц твердой фазы Vчас, а также такими параметрами, как температура частиц Тчас и температура подложки Тподл в момент удара частицы о подложку. При этом под температурой подложки подразумевается не среднемассовая температура обрабатываемой металлоконструкции (подложки), а локальная температура в зоне удара, которая реализуется в процессе диссипации кинетической энергии сверхзвукового гетерогенного потока. Определение указанных выше параметров является необходимым условием как при постановке научных исследований, так и в инженерной практике, например, в цикле крупносерийного производства. Сегодня разработаны методы и средства экспериментального определения этих параметров, например, с использованием сложного наукоемкого оборудования - доплеровских измерителей скорости [7]. Однако применение дорогого оборудования в производстве не всегда целесообразно. Поэтому для управления технологическим процессом формирования покрытий и контролем их качества эффективно использование ЭВМ, снабженных специальным программным обеспечением. Разработка таких программ возможна только при глубоком изучении механизма формирования покрытий и создания математической модели этого процесса [8].
Понятно, что необходимые для формирования покрытий уровни параметров гетерогенных струй формируются, в принципе, в специальном устройстве (стенде). Этот процесс реализуется на всей длине газодинамического тракта стенда. Он начинается в нагревателе газа-носителя и дозаторе порошка, а завершается в главном элементе стенда - сверхзвуковом ускорителе гетерогенной смеси. В ускорителе гетерогенный поток разгоняется до потребных скоростей - газовая фаза до скорости uгаз, твердая фаза (частицы), до скорости Vчас. Известно, что на всей длине ускорителя течение гетерогенной смеси высокоградиентное, поскольку плотность, скорость и температура газа и скорость и температура частиц значительно изменяются вдоль канала.
Таким образом, исследование процесса формирования покрытий газодинамическими методами сопрягается с решением комплекса задач:
- газодинамической задачи течения смеси; - задачи межфазного теплообмена в процессе течения неизотермической гетерогенной смеси в каналах; - задачи тепло - и массообмена при взаимодействии частицы с подложкой.
2.1. Общая математическая модель одномерного течения гетерогенной смеси в ускорителе при наличии межфазного теплообмена.
При постановке задачи под термином «гетерогенная смесь» понималась двухфазная, газопорошковая смесь: газ - носитель + частицы. В такой смеси соотношение массовых концентраций фаз изменялось в пределах: массовая концентрация частиц до 10%, массовая концентрация газовой фазы более 90%. При этом предполагалось, что полидисперсность частиц порошка может варьироваться в пределах 2...20мкм в зависимости от плотности материала частиц.
При такой массовой концентрации фаз течение газовой фазы в ускорителе подчиняется основным положениям механики сплошной среды, а малая масса частиц твердой фазы способствует их перемещению по длине канала в соответствии с законами газовой динамики. Последнее означает, что частицы субмикронного диапазона перемещаются в канале ускорителя по струйкам тока потока газа-носителя.
Кроме того, при разработке математической модели принято, что течение газовой фазы в ускорителе считается одномерным, невязким, изоэнтропическим. Как известно, для такого течения размеры ускорителя и распределение скорости по его длине описываются уравнениями термо- и газодинамики для идеального газа в виде:
- уравнение неразрывности газового потока для критического сечения площадью Fкр:
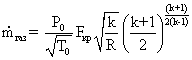 ; (2.1)
; (2.1)
- уравнение корреляции площади произвольных сечений F(x) ускорителя и скорости потока M(x) по оси х сопла:
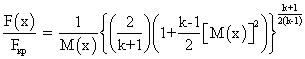 . (2.2)
. (2.2)
При расчете одномерного течения в ускорителе гетерогенной смеси с учетом вязкости газа-носителя использовалась математическая модель, составленная на базе уравнений Новье - Стокса [9] для одномерного стационарного течения каждой из фаз при следующих допущениях:
- - фазы гетерогенной смеси локально однородные;
- - межфазовые превращения отсутствуют;
- - частицы твердой фазы имеют сферическую форму;
- - взаимодействие между частицами отсутствует;
- - отсутствует дробление частиц или их коагуляция;
- - на частицу действует только сила аэродинамического сопротивления газовой фазы.
В такой постановке уравнения сохранения для течения каждой i-ой фазы c массовой концентрацией сi могут быть представлены в виде:
- уравнение неразрывности:
![]() ; (2.3)
; (2.3)
- уравнение движения:
![]() , (2.4)
, (2.4)
где для газовой фазы ![]() , для твердой фазы
, для твердой фазы ![]() , Ri,аэр - сила аэродинамического сопротивления межфазного взаимодействия, описывается соотношением вида:
, Ri,аэр - сила аэродинамического сопротивления межфазного взаимодействия, описывается соотношением вида:
![]() , (2.5)
, (2.5)
где ![]() - изменение плотности газа по длине ускорителя, fмид - площадь миделева сечения частицы, n - число частиц в единице объема
- изменение плотности газа по длине ускорителя, fмид - площадь миделева сечения частицы, n - число частиц в единице объема ![]() , dчас - диаметр частицы,
, dчас - диаметр частицы, ![]() - изменение скорости газовой фазы вдоль сопла,
- изменение скорости газовой фазы вдоль сопла, ![]() - изменение скорости твердой фазы вдоль сопла, Саэр - коэффициент аэродинамического сопротивления сферы субмикронного диапазона, рассчитывается по соотношениям, предложенным в работе [10];
- изменение скорости твердой фазы вдоль сопла, Саэр - коэффициент аэродинамического сопротивления сферы субмикронного диапазона, рассчитывается по соотношениям, предложенным в работе [10];
- уравнение энергии:
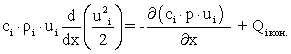 , (2.6)
, (2.6)
где для газовой фазы ui = uгаз, а для твердой фазы ui = Vчас. Qi кон - тепловой поток межфазного конвективного теплообмена в единице объема гетерогенной смеси, т.е. Qi кон = Qкон. - представляется уравнением конвективного теплообмена Ньютона в виде:
![]() , (2.7)
, (2.7)
где ![]() - изменение среднего коэффициента теплоотдачи между газовой и твердой фазами вдоль сопла,
- изменение среднего коэффициента теплоотдачи между газовой и твердой фазами вдоль сопла, ![]() и
и ![]() - изменение температуры газа и частицы вдоль сопла, соответственно,
- изменение температуры газа и частицы вдоль сопла, соответственно, ![]() - площадь боковой поверхности частицы
- площадь боковой поверхности частицы ![]() , как и ранее
, как и ранее ![]() .
.
Записанная система уравнений решается на ЭВМ методом итераций для соответствующих граничных условий.
2.2. Упрощенный алгоритм расчета течения гетерогенной смеси в каналах при наличии межфазного теплообмена
Записанная выше общая математическая модель одномерного течения гетерогенной смеси в каналах представляет собой систему нелинейных дифференциальных уравнений в частных производных. Решение такой системы осуществляется на ЭВМ численными методами с применением специальных программ расчета. При этом в ряде случаев в зависимости от режима течения (ламинарный или турбулентный) используются различные математические модели. Например, применение ![]() модели позволяет рассчитывать турбулентные гетерогенные течения [10]. Понятно, что использование в инженерной практике таких математических моделей и специальных программ для их решения не всегда удобно, поскольку в этом случае требуется специальная математическая подготовка инженеров. Поэтому сегодня все еще остается актуальным решение подобных задач с применением экспресс алгоритмов, базирующихся на применении тривиальных программ и их численного расчета.
модели позволяет рассчитывать турбулентные гетерогенные течения [10]. Понятно, что использование в инженерной практике таких математических моделей и специальных программ для их решения не всегда удобно, поскольку в этом случае требуется специальная математическая подготовка инженеров. Поэтому сегодня все еще остается актуальным решение подобных задач с применением экспресс алгоритмов, базирующихся на применении тривиальных программ и их численного расчета.
В данной работе предложен такой упрощенный алгоритм расчета течения гетерогенной смеси в каналах при наличии межфазного теплообмена.
Предлагаемый упрощенный алгоритм расчета течения базируется на использовании интегральных соотношений второго закона механики Ньютона. В самой простой постановке задачи эти соотношения правомерно использовать в том случае, когда сила, действующая на тело массой m, будет оставаться постоянной в течение всего времени воздействия (экспозиции) ![]() .
.
В анализируемом нами случае телом является частица, масса которой ![]() . Сила, действующая на частицу, по своей природе является аэродинамической силой Rаэр, которая возникает в результате взаимодействия частицы с потоком газа-носителя.
. Сила, действующая на частицу, по своей природе является аэродинамической силой Rаэр, которая возникает в результате взаимодействия частицы с потоком газа-носителя.
Понятно, что в газодинамическом тракте стенда, в силу его функциональных особенностей, Rаэр не будет оставаться постоянной. Поэтому для выполнения указанного выше условия всю длину газодинамического тракта стенда следует разбить на ni элементарных участков длиной DLi, на каждом из которых аэродинамическая сила Rаэр.i ,будет постоянной величиной. На этой концепции построена разработка упрощенного алгоритма расчета газодинамической задачи гетерогенного течения. Конечным результатом расчета с использованием данного алгоритма должно являться изменение скорости газовой фазы uгаз(x) и скорости частиц Vчас(x) на длине каждого из рассчитываемых элементов конструкции газодинамического тракта стенда.
2.2.1. Особенности движения частиц в до- и сверхзвуковых потоках газа-носителя
Будем считать, что частица, инжектируемая в дозвуковой или сверхзвуковой поток газа-носителя, ускоряется только под действием силы аэродинамического сопротивления Rаэр. Как отмечалось, эта сила представляется соотношением (2.5).
Таким образом, расчет кинематики частицы подразумевает:
- расчет ускорения частицы ![]() на каждом i-ом участке элемента;
на каждом i-ом участке элемента;
- расчет времени пролета ![]() частицей расчетного i-го участка;
частицей расчетного i-го участка;
- расчет скорости частицы ![]() в конце каждого i-го участка длиной Li.
в конце каждого i-го участка длиной Li.
Алгоритм расчета ускорения частицы ![]() производится с использованием 2-го закона механики Ньютона в виде:
производится с использованием 2-го закона механики Ньютона в виде: ![]() (2.8), где
(2.8), где ![]() аэродинамическая сила, действующая на частицу на длине расчетного участка ΔLi, определяется по формуле (2.5). Масса частицы
аэродинамическая сила, действующая на частицу на длине расчетного участка ΔLi, определяется по формуле (2.5). Масса частицы ![]() для сферических частиц равна:
для сферических частиц равна: ![]() , где
, где ![]() - плотность материала частицы.
- плотность материала частицы.
Алгоритм расчета времени ![]() пролета расчетного участка длиной Li ускоряющейся частицей осуществляется с использованием формулы для равноускоренного движения:
пролета расчетного участка длиной Li ускоряющейся частицей осуществляется с использованием формулы для равноускоренного движения:
![]() , (2.9)
, (2.9)
где ![]() - скорость частицы на входе в расчетный участок.
- скорость частицы на входе в расчетный участок.
Алгоритм расчета скорости ![]() ускоряющейся частицы в конце расчетного участка осуществляется по формуле:
ускоряющейся частицы в конце расчетного участка осуществляется по формуле:
![]() . (2.10)
. (2.10)
Расчет повторяется для каждого i-го расчетного участка газодинамического тракта.
Следует при этом помнить, что если на длине расчетного участка движение частицы равнозамедленное (например, в диффузоре), в формулах (2.9) и (2.10) ускорение отрицательное.
2.2.2. Алгоритм расчета межфазного теплообмена в гетерогенном потоке
Решение задачи теплообмена между газовой и твердой фазой в гетерогенном потоке сводится к нахождению температуры частиц Тчас перед формированием покрытия, т.е. в момент взаимодействия частицы с подложкой. Определение температуры частицы экспериментальными методами вызывает зачастую непреодолимые трудности, поэтому в инженерной практике широко применяются расчетные методы.
Алгоритм расчета теплообмена в движущейся неизотермической гетерогенной среде строится на базе постулата первого закона термодинамики, записанного для твердого термодинамического рабочего тела (частицы) при отсутствии объемных источников или стоков теплоты. Согласно этому постулату теплота, подведенная к телу через его боковую поверхность, расходуется на изменение энтальпии частицы.
Как отмечалось, в НТГДМ-технологии частицы, из которых формируются покрытия, не претерпевают фазовых переходов, поэтому уравнение первого закона термодинамики в интегральной форме имеет вид:
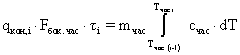 , (2.11)
, (2.11)
где ![]() - конвективный тепловой поток, на единицу боковой поверхности частицы
- конвективный тепловой поток, на единицу боковой поверхности частицы ![]() массой mчас за время
массой mчас за время ![]() пролета частицей i-го расчетного участка длиной DLi. Согласно закону конвективного теплообмена Ньютона
пролета частицей i-го расчетного участка длиной DLi. Согласно закону конвективного теплообмена Ньютона ![]() представляется в виде:
представляется в виде:
![]() , (2.12)
, (2.12)
где Тгаз.i - температура газа-носителя на длине расчетного i-го участка длиной DLi,![]() - средняя температура частицы в на длине i-го участка,
- средняя температура частицы в на длине i-го участка,![]() ,
, ![]() - коэффициент теплоотдачи на расчетном i-ом участке, счас.i - удел0ная теплоемкость материала частицы при температуре
- коэффициент теплоотдачи на расчетном i-ом участке, счас.i - удел0ная теплоемкость материала частицы при температуре ![]() . С учетом указанного, уравнение (2.11) принимает вид:
. С учетом указанного, уравнение (2.11) принимает вид:
![]() , (2.13)
, (2.13)
Из теории конвективного теплообмена известно, что коэффициент теплоотдачи между газовой и твердой фазой ![]() можно определить из соотношения критерия Нуссельта, т.е.:
можно определить из соотношения критерия Нуссельта, т.е.:
![]() . (2.14)
. (2.14)
В свою очередь, критерий ![]() представляется критериальным соотношением типа:
представляется критериальным соотношением типа:
![]() , (2.15)
, (2.15)
где индекс «w» означает, что для данного критерия определяющей температурой является температура частицы на расчетном i-ом участке. При этом критерий Рейнольдса 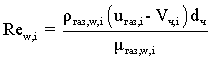 , критерий Нуссельта
, критерий Нуссельта ![]() представляется соотношением (2.14), критерий Прандтля
представляется соотношением (2.14), критерий Прандтля 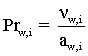 . Здесь dчас - диаметр частицы. Остальные параметры общепринятые.
. Здесь dчас - диаметр частицы. Остальные параметры общепринятые.
Из (2.13) следует:
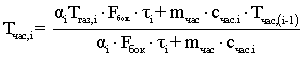 , (2.16)
, (2.16)
где ![]() - температура частицы на предыдущем расчетном участке,
- температура частицы на предыдущем расчетном участке, ![]() - время пролета частицей расчетного участка, рассчитывается с использованием формулы (2.9).
- время пролета частицей расчетного участка, рассчитывается с использованием формулы (2.9).
Поскольку в выражении (2.16) все параметры зависят от искомой температуры поверхности, то расчет ![]() проводится методом последовательных приближений.
проводится методом последовательных приближений.
Результаты расчета по длине ускорителя изменения скорости газового потока uгаз, а также скорости Vчас и температуры Тчас частицы с использованием общей и предложенной упрощенной математических моделей приведены на рис. 1.
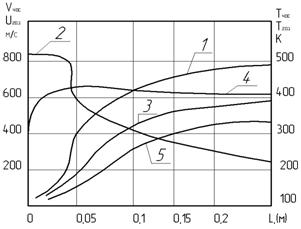
Рис. 1. Результаты расчета по длине ускорителя изменения скорости газового потока uгаз, а также скорости Vчас и температуры Тчас частицы с использованием общей и предложенной упрощенной математических моделей
1 - скорость газовой фазы, 2 - температура газовой фазы, 3 - скорость частицы из Al, 4 - температура частицы из Al, 5- температура частицы из Al диаметром 80 мкм.
По изложенным в разделах 2.1 и 2.2 методикам проведен расчет динамики течения частиц и межфазного теплообмена в гетерогенном потоке. Род газовой фазы - воздух, твердая фаза - частицы из Al диаметром 40 мкм. Форма ускорителя - коническое сопло Лаваля. Результаты расчета приведены на рис. 1.
Из приведенных данных следует, что максимальный темп нагрева частицы реализуется в докритической области сопла, т.е. в области максимальной температуры и плотности газа. Кроме того, на интенсивность нагрева частицы в докритической части сопла оказывает сильное влияние то обстоятельство, что в этой части сопла частицы находятся относительно долго вследствие малости скоростей газовой uгаз и твердой Vчас фаз.
Как следует из приведенных данных, температура частиц алюминия и меди близки по уровню на всей траектории движения (кривые 5 и 6), несмотря на заметное различие в скоростях (кривые 3 и 4).
Из приведенных расчетных данных также следует, что на уровень температуры род материала частиц оказывает влияние в меньшей степени (см. кривые 5 и 6), чем их размер частиц (см. кривые 5, 7). Кривая 7 соответствует температуре сферической частицы из алюминия с радиусом, в два раза большим, чем в варианте, рассмотренном ранее.
СПИСОК ЛИТЕРАТУРЫ:
- 1. Способ получения покрытий. Ю.В. Дикун, Ю.А. Кочерин, П.В. Никитин, Ю.П. Фролов. Патент RU, № 2082823 от 17.06.1991 г.
- 2. Никитин П.В., Кочерин Ю.А., Дикун Ю.В. Взаимодействие двухфазных потоков с преградой // Сб. трудов МАИ: «Исследование теплообмена в ЛА». М.: МАИ, 1982, с. 16.
- 3. Кудинов В.В. //Плазменные покрытия. М.: Наука, 1977. 183 с.
- 4. Харламов Ю.Н., Кудинов В.В. и др. //Применение детонации в газах для нанесения покрытий. Физика горения и взрыва (СО АН СССР). 1975. № 1. с. 88.
- 5. Михатулин Д.С., Полежаев Ю.В., Репин И.В. //Гетерогенные потоки: газодинамика, теплообмен, эрозия. М., 1997. (Препринт /ИВТАН, №2 - 402).
- 6. Устройство для формирования покрытий. П.В. Никитин, Ю.В. Дикун, Ю.П. и др. Патент RU, № 2089665 от 23.06.1995 г.
- 7. Под ред. В.А. // Фабриканта Лазерная диагностика потоков. - М.: Изд-во МЭИ, 1990. 287 с.143
- 8. Андреев Н.А., Давыдов Н.Н., Никитин П.В., Смолин А.Г. // Автоматизированный комплекс сбора и обработки экспериментальных данных при исследовании процессов тепломассообмена в гомогенных и гетерогенных высокотемпературных газовых потоках. Доклад. 3-ий Минский международный форум по тепло - и массообмену. Минск, 1996.
- 9. Лепешинский И.А. // Газодинамика одно- и двухфазных течений в реактивных двигателях. М. Издательство МАИ. 2003.
- 10. Henderson, C. B., AIAA Journal 14, 707, 1976.



