Введение
В настоящее время все чаще в радиолокационных станциях (РЛС) низковысотного обнаружения используются широкополосные и многочастотные сигналы [6, 7] в связи с их явными преимуществами в разрешающей способности и снижении влияния пассивных помех. Сигналы с аналогичной структурой используются и в системах связи различного назначения, в том числе в системах сотовой связи, спутниковой связи.
Возрастание требований к качеству функционирования радиотехнических систем, а именно к качеству предоставляемого ими сервиса, предопределяет необходимость поиска новых высокоэффективных алгоритмов управления качеством сервиса в реальных условиях эксплуатации радиотехнических систем.
Одним из наиболее незадействованных потенциалов современных радиотехнических систем, способным оказать существенное влияние на качество сервиса, остается энергетический потенциал антенных систем, являющихся обязательным элементом любой радиотехнической системы [4, 5].
Возможность управления энергетическим потенциалом антенны, что особенно характерно для антенных решеток, позволяет перераспределять мощность излучаемых сигналов в заданные направления, а также минимизировать возможные воздействия на приемные системы мешающих или помеховых сигналов.
Цель статьи – разработка метода матричного синтеза широкополосных антенных решеток с учетом ограничений на форму диаграммы направленности на различных частотах функционирования решетки, т.е. разработка метода компромиссного синтеза.
Допустим, что требуется синтезировать многофункциональную антенную решетку (АР) с комплексным управлением, функционирующую в заданном диапазоне частот 
, тогда расширенный обобщенный энергетический функционал [5] имеет вид:
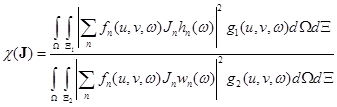, (1)
в котором 
– парциальная диаграмма, полученная при возбуждении n-го элемента АР волной единичной амплитуды и нулевой фазы на частоте 
; 
, 
, 
и 
– частотно зависимые весовые функции, аналогичные весовым функциям функционала [2]; n=1,2,…,N; N – число элементов в антенной решетке.
Учитывая, что на комплексные амплитуды токов синтезируемой широкополосной АР накладывается ограничение 
, получим эквивалентную матричную форму для функционала (1):
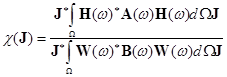, (2)
где 
и 
– эрмитовы матрицы с элементами:
, (3)
. (4)
а 
и 
– частотно-зависимые матрицы преобразований N-го порядка.
Таким образом, задача матричного синтеза широкополосной АР сводится к задаче определения такого вектора комплексных амплитуд токов 
в элементах АР, который обеспечивает экстремум выбранного функционала в полосе частот [1].
Постановка и алгоритм решения задачи компромиссного синтеза
Сформулируем задачу синтеза: максимизировать функционал (1) с учетом группы линейных ограничений при изменении комплексных амплитуд токов во всех элементах антенной системы:
. (5)
В задаче (5) наряду с максимизацией функционала 
требуется учесть ряд линейных ограничений, задаваемых в общем виде матричным преобразованием 
. Поскольку каждое ограничение должно выполняться в полосе частот , проинтегрируем матрицу 
по частоте, тогда вместо получим 
, где 
. В данном случае матрица 
– матрица, 
-ой строкой которой формируется ограничение.
Удовлетворение каждого из К ограничений уменьшает число степеней свободы вектора 
на единицу, тогда исходный вектор токов связан с новым вектором токов 
преобразованием:
. (6)
Подставим (6) в (1) и получим преобразованный функционал с учетом К линейных ограничений:
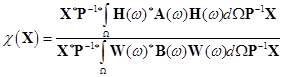. (7)
Так как К проекций вектора равны нулю, то для дальнейшего решения задачи синтеза из (4) исключаются К элементов вектора и К строк и столбов матриц 
и 
соответственно, а решением задачи синтеза будет вектор 
, удовлетворяющий равенству:
, (8)
где
;
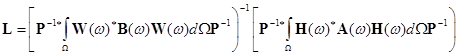– максимальное собственное число пучка форм, образуемого отношением (7). Обозначение 
имеет смысл исключения К строк и К столбцов из соответствующих матриц.
Результаты моделирования
Моделирование проводилось на примере линейной АР изотропных излучателей с параметрами: N=91; межэлементное расстояние 
, направление главного максимума 
. Решетка функционирует на частотах 
, 
и 
. Рабочая полоса частот 
(
– нижнее и верхнее значения рабочей полосы частот АР). В качестве ограничений рассмотрим ограничения на уровень ДН в рабочей полосе частот в направлении на источник пассивных помех. Будем полагать, что это направление: 
. Таким образом, в случае точечного источника помех необходимо задачу синтеза дополнить М ограничениями, обеспечивающими снижение уровня ДН антенной решетки во всей полосе частот.
На рис. 1–3 представлены ДН АР, синтезированные предложенным (непрерывная линия) и известным [1] (штриховая линия) методами.
Рис. 1 соответствует центральной частоте , рис. 2 – частоте 
, рис. 3 – 
. На рис. 1–3 вертикальной линией отмечено направление воздействия помехи.
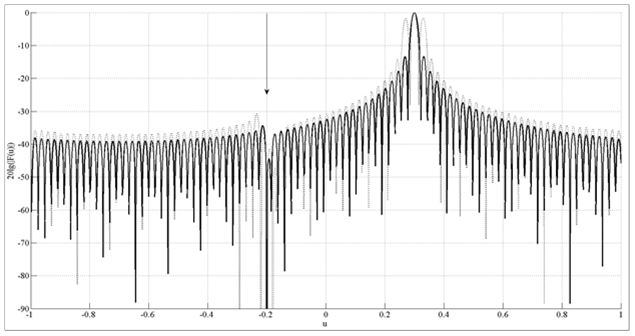
Рис. 1. Синтезированные диаграммы направленности на частоте
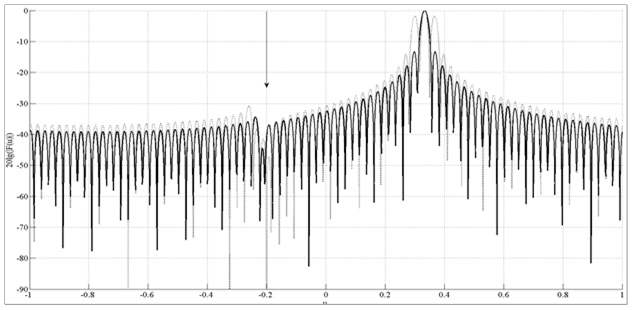
Рис. 2. Синтезированные диаграммы направленности на частоте
Рис. 3. Синтезированные диаграммы направленности на частоте
Из рис. 1–3 видно, что при изменении частоты (в соответствии с известной угло-частотной зависимостью) направление главного максимума ДН смещается, что соответствует снижению мощности излучения в заданном направлении. В случае решения задачи синтеза известным методом [1] мощность излучения снижается до уровня излучения, сопоставимого с уровнем излучения антенны, по первым боковым лепесткам (что соответствует уменьшению коэффициента направленного действия АР на 10 и более дБ). Применение же предложенного метода уменьшает энергетический потенциал АР на величину не более чем на 2 дБ.
Выводы
Таким образом, предложенный метод компромиссного матричного синтеза широкополосных антенных решеток на основе расширенного обобщенного энергетического функционала позволяет максимизировать энергетические параметры антенной решетки в заданной рабочей полосе частот, что невозможно при применении известных решений.
Исследование проведено при поддержке Министерства образования и науки Российской Федерации, соглашение 14В37.21.2067
Рецензенты:
Звездина Марина Юрьевна, доктор физико-математических наук, доцент, заведующая кафедрой "Радиоэлектроника", Минобрнауки России, Ростовский технологический институт сервиса и туризма (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», г. Ростов-на-Дону.
Мищенко Сергей Евгеньевич, доктор технических наук, профессор, ведущий научный сотрудник, Федеральное государственное унитарное предприятие "Ростовский научно-исследовательский институт радиосвязи" Федеральный научно-производственный центр, г. Ростов-на-Дону.