I. Особенности течения гетерогенной смеси в микросоплах с большим удлинением
Из большого количества задач, которые приходится решать при формировании защитных покрытий газодинамическими методами, следует выделить две проблемные, играющие определяющую роль в синтезе покрытий высокого качества [2]:
- - формирование течения гетерогенной смеси в газодинамическом тракте и ускорителях с большим удлинением;
- - взаимодействие высокоскоростной частицы субмикронных размеров с твердой поверхностью.
Первая из указанных задач связана, главным образом, с динамикой ускорения в высокоскоростном газе-носителе твердой фазы (частиц), формирующих покрытие. Этот процесс реализуется в потоке вязкого газа, истекающего с ускорением в специальных профилированных по законам газовой динамики каналах - сопловых насадках или ускорителях. Задача усложняется тем, что для получения потребной скорости частиц на выходе из ускорителя, сопловые насадки должны снабжаться не только расчетным профилем, но и должны иметь соответствующую удлиненную форму. Это связано, прежде всего, с тем, что длина канала определяет скорость частиц, а вместе с тем и важнейшие показатели технологического процесса нанесения покрытий, такие как качество покрытия, производительность, коэффициент использования порошка, и т. д. [3].
Как известно из газовой динамики, вязкое течение газа в каналах сопровождается образованием нарастающего по толщине пограничного слоя. Этот процесс деформирует поле скоростей как поперек, так и по длине канала, что в случае течения в нем гетерогенной смеси оказывает заметное влияние на кинематику частиц. Поэтому разработка методики проектирования ускоряющих каналов с целью получения двухфазных потоков с оптимальными параметрами является актуальной.
Вторая из указанных проблемных задач связана с взаимодействием высокоскоростных частиц малого размера с твердой поверхностью. Из механики твердого тела известно, что ударное приложение нагрузки вызывает в твердом теле образование ударных волн, их интерференцию и другие процессы. В этом случае в местах локализации волн реализуются процессы упругой и пластической деформации, адиабатическое преобразование механической энергии в теплоту, ее диссипация, динамическая диффузия, а также возможные фазовые и структурные изменения. В итоге, весь этот комплекс процессов формирует многопараметрическую задачу, решение которой позволит создать оптимальную технологию формирования высококачественных покрытий, обладающих целенаправленными функциональными свойствами.
Как отмечалось, важнейшим элементом технологических установок для нанесения покрытий является профилированный канал, в котором происходит ускорение гетерогенного потока. В реальных установках применяются удлиненные ускоряющие каналы (сопла Лаваля) конической или плоской, прямоугольной формы с малыми углами раскрытия сверхзвуковой части. В связи с малыми площадями критических сечений (dkp = 1...5 мм) относительное удлинение таких каналов может изменяться в широких пределах (L/dkp = 50...200).
Основная особенность течений вязких газов в соплах удлиненных форм заключается в том, что образовавшийся на поверхности стенок канала пограничный слой существенно уменьшает фактическое проходное сечение сопла по сравнению с расчетным, технологическим сечением. Это снижает массовый секундный расход потока, т.е. его скорость. Если при проектировании таких каналов не учитывать этот эффект, то пограничный слой смыкается внутри сопла и далее, вниз по потоку, возникает установившееся турбулентное течение, подобное тому, которое реализуется на основном участке гладкой цилиндрической трубы. Как известно, такое течение сопровождается интенсивной диссипацией энергии потока.
При течении гетерогенных смесей в ускорителях таких форм из-за малости размеров частиц (субмикронный диапазон) их движение вдоль каналов можно считать прямолинейным. Возникшая турбулизация потока в силу указанных выше причин изменяет как характер движения частиц, так и закон распределения скорости частиц по поперечному сечению потока. Кроме того, эффект диссипации энергии заметно уменьшает скорость частиц по сравнению с расчетной. Например, экспериментально установлено, что скорость частиц в двухфазных потоках, измеренная лазерным доплеровским измерителем скорости, может существенно (до 50%) отличаться от значений, рассчитанных по теории адиабатических течений. Вот почему появилась необходимость оценки влияния пограничного слоя на динамику течения гетерогенной смеси в каналах удлиненной формы.
При проведении такого анализа принимался ряд допущений. Например, вследствие малости размеров частиц перепад температуры в их объеме не учитывался. Последнее близко к реальным условиям, поскольку по оценкам величина критерия Био изменяется в пределах Bi = 10-3...10-4. Кроме того, считалось, что вязкостные эффекты, которые, в общем, зависят от температуры поверхности, в связи с низкими уровнями величин температуры частиц не оказывают существенного влияния на аэродинамическое сопротивление частицы. Это позволило при анализе в рамках приближенной модели межфазного взаимодействия частицы и газового потока, рассматривать динамическую и тепловую задачи, как две независимые.
В такой постановке алгоритм расчета параметров потока вязкого газа был составлен на базе использования классической модели плоского пограничного слоя [4]. При этом динамическая задача представлялась системой интегро-дифференциальных уравнений в виде:
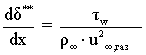 (1.1).
(1.1).
Как известно, число Маха набегающего потока ![]() , а также температурный фактор
, а также температурный фактор ![]() и число Рейнольдса Rew слабо влияют на форму профиля скоростей по толщине пограничного слоя, то предполагалось, что:
и число Рейнольдса Rew слабо влияют на форму профиля скоростей по толщине пограничного слоя, то предполагалось, что:
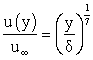 (1.2).
(1.2).
В таком случае, связь между интегральными характеристиками пограничного слоя определялась в виде:
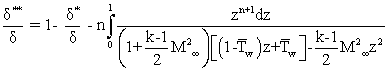 (1.3)
(1.3)
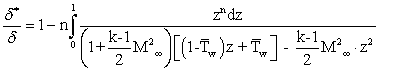 (1.4).
(1.4).
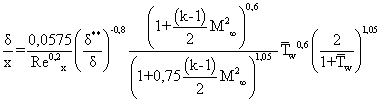 (1.5)
(1.5)
Представленная выше система уравнений пограничного слоя позволила рассчитать сверхзвуковые течения, полученные в реальных сверхзвуковых ускорителях (соплах удлиненных форм). Исходными данными для расчета являлись параметры торможения потока Р0, Т0 и геометрические размеры сопл.
Таблица 1. Результаты расчетов
|
dкр |
dср |
Mср.ф |
Reх |
Mср.р |
dср.ф/dср.р |
Mср.эк |
|
мм |
мм |
- |
- |
- |
- |
- |
|
3,5 |
12,2 |
3,45 |
6,3×105 |
4,14 |
0,71 |
- |
|
4,5 |
9,5 |
2,55 |
4,36×105 |
3,05 |
0,84 |
2,48 |
|
4,5 |
9,5 |
2,67 |
5,19×105 |
3,05 |
0,845 |
2,6 |
|
2,72 |
12,65 |
3,87 |
1,2×105 |
4,8 |
0,67 |
- |
|
4,72 |
12,65 |
2,84 |
0,27×105 |
3,58 |
0,71 |
- |
В таблице 1 приведены некоторые результаты расчетов. В частности, обращают на себя внимание соотношения между фактическими диаметрами выходного сечения сопла dср.ф к его расчетному, технологическому диаметру dср.р, а также отношение фактического числа Маха Мср.ф к его значению, рассчитанному по адиабатической теории идеального течения Мср.ад. и числу Маха, полученному экспериментально для данного сопла Mср.эк. Для сравнения в таблице последние две строки представляют данные работы [5]. Результаты удовлетворительно коррелируются друг с другом. Видно, заметное влияние нарастания толщины пограничного слоя на характер течения вязкого газа в удлиненных соплах.
Проведенные расчеты с использованием представленной выше системы уравнений (1.1)...(1.5) показывают, что, например, в коническом сопле с диаметром критики dкp = 1 мм пограничный слой смыкается на расстоянии L = 10... 12 мм от критического сечения. При увеличении диаметра критики сопла до dкp = 2 мм пограничный слой смыкается уже на расстоянии L = 100...120 мм. Далее, в низ по потоку в обоих соплах устанавливается турбулентное течение. Данное обстоятельство существенно усложняет применение микросопл в технологических установках. Их проектирование необходимо осуществлять с учетом нарастания толщины пограничного слоя вдоль стенок ускорителя частиц.
II. Динамика движения частиц твердой фазы в микросоплах удлиненной формы
Как известно, ускорение частиц в гетерогенном потоке определяется характеристиками потока газа-носителя (его скоростью uгаз, плотностью ρгаз и др.), а также размерами частиц и родом их материала. Кроме того, важную роль в этом процессе играет характер течения газа-носителя в канале ускорителя.
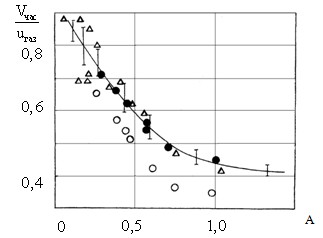
Рис. 1. Изменение относительной скорости частицы от безразмерного комплекса параметров А.![]() ,Lуск - длина ускорителя, Р0-давление в расчетном сечении ускорителя, --- расчет /раб. 5/, Δ - эксперимент /раб. 5/, Ο - результаты данной работы Сf = 0,5, ● - результаты данной работы Сf = 1,0.
,Lуск - длина ускорителя, Р0-давление в расчетном сечении ускорителя, --- расчет /раб. 5/, Δ - эксперимент /раб. 5/, Ο - результаты данной работы Сf = 0,5, ● - результаты данной работы Сf = 1,0.
На рис. 1 представлены результаты расчетов и измерений относительной скорости частиц алюминия и меди в сопоставлении с результатами работы [5]. В экспериментах применялись промышленные порошки с дисперсностью Rчас = (2,5...25)∙10-6 м. Скорость потока варьировалась в пределах W = 200...1200 м/сек.
На рис. 1 представлены результаты численного эксперимента, проведенного в МАИ по изложенной выше методике. Условия эксперимента аналогичны данным работы [5], за исключением того, что в нашем случае расчеты выполнены для конического сопла.
Основная сложность применения данной методики, на наш взгляд, заключается в том, что форма частиц промышленных порошков, используемых в экспериментальной и технологической практике, существенно отличается от сферической, для которых зависимость Cf от Rеw известна. Этим можно объяснить расхождение результатов расчета относительной скорости для сферических частиц с Cf = 0.5. На рис.1 приведены результаты расчетов для частиц несферической формы при Cf =1,0. Как видно, при Cf =1,0 наблюдается хорошая корреляция результатов обеих работ.
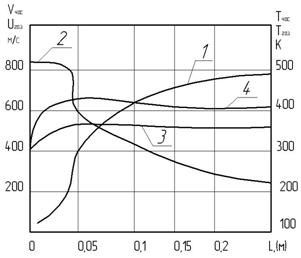
Рис. 2. Распределение скорости и температуры газовой и твердой фаз по длине сверхзвукового ускорителя
1 - скорость газовой фазы, 2 - температура газовой фазы, 3 - скорость частицы из Cu, 4 -температура частицы из Cu
По изложенному в разделе 1 алгоритму проведен расчет динамики течения частиц и межфазного теплообмена в высокоскоростном гетерогенном потоке. Род газовой фазы - воздух, твердая фаза - частицы из меди Cu диаметром 40 мкм. Форма ускорителя - коническое сопло Лаваля. Результаты расчета представлены на рис. 2.
Из приведенных данных следует, что максимальный темп нагрева частицы реализуется в докритической области сопла, т.е. в области максимальной температуры и плотности газа-носителя. Кроме того, на интенсивность нагрева частицы в докритической части сопла оказывает сильное влияние то обстоятельство, что в этой части сопла частицы находятся относительно долго вследствие малости скоростей газовой uгаз и твердой Vчас фаз.
СПИСОК ЛИТЕРАТУРЫ:
- 1.Никитин П.В., Степаненко С.А. //«Низкотемпературный газодинамический метод формирования разнофункциональных покрытий на поверхностях конструкций». Доклад на 5-й международной кнференции «Авиация и космонавтика - 2006». Москва, 2006.
- 2. Полежаев Ю.В., Михатулин Д.С., Никитин П.В. //«Моделирование межфазного обмена в гетерогенных средах с целью разработки высокоэффективных технологий». ИФЖ, т.71, №1, с.19...29.
- 3.Никитин П.В., Кочерин Ю.А., Дикун Ю.В. //Взаимодействие двухфазных потоков с преградой //Сб. трудов МАИ: «Исследование теплообмена в ЛА». М.: МАИ, 1982, с. 16.
- 4. Авдуевский В.С., Галицейский Б.М., Данилов Ю.И. и др. //«Основы теплопередачи в авиационной и ракетно-космической технике». М.: Машиностроение. 1992, 700 с.
- 5. Алхимов А.П., Клинков С.В., Косырев В.Ф. //Течение в сверхзвуковом сопле большого удлинения с прямоугольным сечением. «Теплофизика и аэромеханика».



