Введение. Для многих машин эксплуатационная надежность определяется триботехническим качеством узлов трения. Шероховатость на их рабочих поверхностях обусловливает весьма малую фактическую площадь контакта. Под нагрузкой это вызывает значительную деформацию контактирующих микронеровностей, которая во многих случаях является пластической. Пластическая деформация всегда имеет место на поверхности относительно мягких антифрикционных сплавов подшипников скольжения при технологической приработке двигателей внутреннего сгорания (ДВС), при неустановившихся и переходных режимах их работы. Перегрузка поверхности приводит к «опасному» уровню пластической деформации, обусловливающему появление повреждений, их развитие, заедание. Однако к настоящему времени закономерности пластического деформирования при трении мало изучены. Поэтому сложившиеся общие представления о деформации поверхностных слоев для реальных трибосопряжений не дают достаточно конкретных рекомендаций. Закономерности микромеханики пластического деформирования нагруженных поверхностей при трении также могут быть полезны при технологическом влиянии на размеры пластически деформированного слоя при выполнении операций поверхностного пластического деформирования – накатывании, выглаживании и т. п.
Целью работы является математическое моделирование и установление закономерностей и диапазона условий распространения пластически деформированной области в поверхностном слое нагруженного тела.
Теоретическое содержание. Применительно к подшипникам скольжения использование метода построения линий скольжения показало, что с насыщенностью микронеровностей, соответствующей реальным поверхностям, при пластическом деформировании происходит смыкание и перекрытие деформированных участков под ними. Поэтому в подповерхностном слое при трении происходит распространение деформированной области по глубине. В случае стесненной деформации, что имеет место при трении, под поверхностью контакта образуется зона деформации с напряжениями, значительно превышающими предел текучести материала. Вследствие наличия внешней тангенциальной силы трения «опасный» очаг деформации смещается в сторону движения с выходом на поверхность, что приводит к ее разрушению[6].
Знание закономерностей и факторов формирования размеров пластически деформированной области позволит избежать перегрузки трущихся поверхностей в процессе технологической приработки ДВС и обеспечить им более высокое триботехническое качество.
Важное значение на условия пластического деформирования оказывают геометрические параметры контакта. Поэтому при изучении взаимодействия шероховатых поверхностей микронеровности моделируют телами правильной формы, в определенной мере соответствующей реальным микронеровностям. В проводимом математическом моделировании за эквивалент микронеровности был принят жесткий конус, движущийся по жестко-пластическому полупространству, подчиняющемуся условию пластичности Треска. При этом учитывалось, что для металлических поверхностей углы наклона сторон микронеровностей к поверхности трения, зависят от вида обработки, степени приработанности и составляют угол 5…30° [5]. Принималось, что распределение материала в шероховатом профиле контртела описывается уравнением опорной кривой. Важной особенностью считалось наличие взаимного влияния соседних микронеровностей в процессе деформирования.
Согласно принятой модели микронеровность внедрена в полупространство на величину а , движется под действием касательной силы и деформирует полупространство на глубину h. В моделировании использовался метод баланса работ пластической деформации, предполагающий рассмотрение главных напряжений [4]. При этом считается, что на распределение напряжений касательная сила не влияет, но механические свойства материала определяются наличием деформации, скоростью деформирования и температурой, которые могут вызвать упрочнение и разупрочнение. Возможность учета перечисленных явлений обеспечивает используемому методу расчета преимущество по сравнению с другими методами. В решении использовалось уравнение баланса работ внешних и внутренних сил
![]() , (1)
, (1)
где А – работа внешней силы, АД – работа деформации материала, АТ– работа силы трения на контактной поверхности.
Работа внешней силы определялась через элементарное перемещение микронеровности, для определения АД и АТ использовались уравнения работ для плоского деформирования
![]() , (2)
, (2)
![]() , (3)
, (3)
где si – интенсивность напряжений, ei – интенсивность деформаций, dV – объем элементарного деформируемого участка, tк – средняя удельная сила трения, u – перемещение, dS – дифференциал площади контакта.
Совместное решение уравнений (1), (2), (3) с учетом геометрических соотношений, условия несжимаемости и закона Зибеля позволило представить уравнение баланса работ при пластическом деформировании как условие пластического равновесия поверхностного слоя
![]() , (4)
, (4)
где t - касательное напряжение, ss – истинное напряжение текучести материала полупространства, m - коэффициент контактного трения, ![]() - угол между боковой поверхностью микронеровности и полупространством, h - глубина деформированного слоя,
- угол между боковой поверхностью микронеровности и полупространством, h - глубина деформированного слоя, ![]() - безразмерная характеристика трибодеформации, зависящая от а и h , семейства решений которой получены с помощью ПЭВМ.
- безразмерная характеристика трибодеформации, зависящая от а и h , семейства решений которой получены с помощью ПЭВМ.
Достоверность условия (4) подтверждается результатами изучения образцов алюминиево-оловянных подшипниковых сплавов с разным содержанием олова, прошедших приработку в равных условиях, методом рентгено-структурного анализа по глубине распространения пластического деформирования в алюминиевой матрице (основе) сплавов (рис. 1).
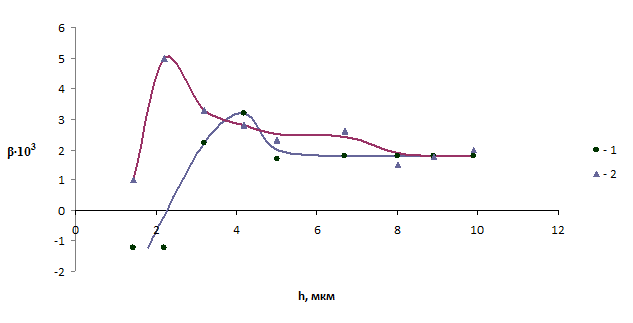
Рис.1. Изменение уровня пластического деформирования по глубине для подшипниковых сплавов: с 3% олова (1), с 50% олова (2).
Мерой искаженности микростроения от пластического деформирования являлось физическое уширение интерфференционных линий β материала основы. У сплава, с 3% олова (кривая 1), глубина распространения пластического деформирования и уровень деформации оказались меньше, чем у сплава с 50 % олова (кривая 2), имеющего меньший коэффициент контактного трения, что согласуется с условием пластического равновесия (4). Результаты расчета и рентгено-структурного анализа по глубине деформированного слоя совпали не только качественно, но и оказались достаточно близкими по величине.
Применение к условиям технологической приработки. Приработка подшипников всегда сопровождается пластическим деформированием антифрикционного слоя. Между возвышающимися исходными микронеровностями на отдельных участках поверхности материала подшипника и более гладкой и жесткой поверхностью вала возникает пластический контакт (по фактической площади касания) с соответствующим уровнем коэффициента контактного трения µ. При достижении напряжения текучести в выступающих неровностях материала подшипника начинается пластическое деформирование с распространением его до определенной глубины. Благодаря этому неровности пластически оседают и в контакт вступают другие менее высокие неровности. Вследствие гетерогенности микроструктуры, барьеров в движении дислокаций, различных механизмов (систем) скольжения глубина проникновения пластического деформирования конечна. Ограниченность толщины деформируемого слоя делает правдоподобным предположение о пластическом течении материала в пределах еще не приработанных микровыступов достаточно пластичных и быстро разупрочняющихся от фрикционного нагрева (или вообще не упрочняющихся) подшипниковых материалов типа баббитов и сплавов на основе алюминия. Тем более, что у исходных микровыступов соотношение средних значений высоты и основания составляет от 1:12 до 1:20, т.е., выступы представляют собой участки с достаточной протяженностью и, особенно, в направлении движения [1]. Поэтому пластическим течением может быть охвачен и подповерхностный слой. Таким образом, распространение области пластического деформирования по глубине и увеличение размеров этой области от повышающейся нагрузки в объеме микронеровности (или в подповерхностном слое) могут провести к разрушению микронеровности (или материала в подслое) и отделению фрагментов материала подшипника. Отмеченное позволяет предположить существование некоторого критического значения глубины пластически деформированной области как в не приработанных (не осевших и не полностью изношенных) микровыступах, так и на почти приработанных участках поверхности. Непривышение критической глубины деформированного объема позволит избежать разрушения поверхности при прохождении процесса технологической приработки.
Подповерхностное пластическое течение в обоих случаях может начаться и при наличии смазки. Для этого необходимо только, чтобы действующее касательное напряжение τ в контакте достигло уровня τmax = k (где τmax -максимальное главное касательное напряжение; k - постоянная пластичности). Т.е. необходимо лишь, чтобы коэффициент контактного трения μ был достаточным по величине, что возможно при повышающихся в технологической приработке нормальных напряжениях, так как τmax при этом постоянно. Снижению μ, в достаточных для пластического течения пределах, способствует пластическое вытеснение мягких металлических составляющих в алюминиево-оловянных и алюминево-свинцовых сплавах при приработке, установленного экспериментально.
Расчеты с использованием условия пластического равновесия поверхностного слоя (4) показали, что при геометрических параметрах контакта, соответствующим реальным поверхностям, пластическое течение возможно при угле α от 2о до 25о. При α < 2о требуются практически недостижимые значения μ, при α > 25о - наступает микрорезание. Установлено, что величина внедрения a линейно влияет на глубину деформированной области. Уменьшение угла α и коэффициента контактного трения µ, сопровождающее приработку, увеличивает глубину деформированного подслоя. Взаимодействие прирабатываемых поверхностей при постоянном (критическом) значении толщины пластического подслоя возможно при уменьшении µ до 0,1 при α = 20о и – до 0,41 при α = 5о.
Таким образом, оценка границ области существования пластического деформирования поверхности при реальных параметрах контакта показала, что пластическое течение в подповерхностном слое подшипниковых сплавов при приработке возможно.
Заключение. Математическое моделирование позволило определить направление и степень влияния параметров контакта на глубину деформирования, оценить границы области протекания процесса и начала разрушения в диапазоне изменения параметров контакта, соответствующем подшипникам скольжения ДВС в период технологической приработки. Отмеченное было использовано при разработке основ изофрикционной приработки подшипников скольжения как более эффективной технологии [2,3].
Рецензенты:
Андрианов Д.Е., д.т.н., профессор, зам.директора по учебной работе Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный университет им. Александра Григорьевича и Николая Григорьевича Столетовых», г.Муром.
Соловьев Д.Л., д.т.н., профессор, профессор кафедры «Автоматизированное проектирование машин Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный университет им. Александра Григорьевича и Николая Григорьевича Столетовых», г.Муром.



