Введение. Всякое представление натурального числа суммой натуральных чисел называется разбиением числа. Разбиения изучаются в задачах, прежде всего, комбинаторного и теоретико-числового характера. К классическим комбинаторным относятся задачи подсчета и перечисления разбиений данного типа, в теории чисел решают проблемы об аддитивных представлениях чисел с арифметическими ограничениями на слагаемые. В этой статье мы изучаем вопросы, связанные с подсчетом числа так называемых совершенных и идеальных разбиений натурального числа, устанавливаем новые рекуррентные соотношения для подсчета числа таких разбиений для чисел специального вида.
Идеальные и совершенные разбиения. Понятие идеального разбиения (sub-perfect partition) числа ввел П. Мак-Магон [4], решая так называемую обобщенную задачу Баше о гирях: найти всевозможные наборы гирь (необязательно разных), с помощью которых можно взвесить любой груз в целое число граммов от 1 до M включительно, если гири разрешается ставить на обе чашки весов. При этом существенно, что каждое взвешивание должно осуществляться единственным образом. Например, если M = 40, то с помощью набора из четырех гирь в 1, 3, 9 и 27 граммов можно взвесить единственным способом любой груз от 1 до 40 граммов включительно. Указанный набор гирь не является единственным. Всего имеется восемь наборов гирь, позволяющих отвесить любое целое число граммов от 1 до 40 при условии, что гири можно ставить на обе чашки весов: 140; 11313; 1494; 113194; 113271; 1134271; 1491271; 113191271. (Здесь wm обозначает m гирь весом w каждая.) Среди этих решений только последний набор содержит наименьшее число гирь и только в нём одном все гири разные.
Обобщенная задача Баше о нахождении наборов гирь для конкретных чисел M встречалась на математических олимпиадах школьников разного уровня, а также на одном из командных соревнований по программированию среди студенческих команд. Для эффективного решения задачи необходимо, по сути, составить рекурсивный алгоритм, с помощью которого вычисление общего количества таких наборов сводится к аналогичной задаче о подсчете числа разбиений меньшего числа M′.
Перейдем к решению задачи в общей постановке. Разбиение неотрицательного целого числа M = m1 + m2 + ... + ms назовем идеальным, если каждое целое число m от 0 до M можно представить единственным образом в виде m = a1m1 + a2m2 + ... + asms , где каждое ai Î {–1, 0, 1}, при этом повторяющиеся части mi считаются неразличимыми. Если все части разбиения mi рассматривать как разновесы для весов, каждое такое представление указывает единственный способ взвешивания массы m с помощью гирь массой mi . При этом ai = 0 означает, что гиря с массой mi не участвует во взвешивании, а в случае ai = –1 (ai = 1) гиря mi находится на той же (на другой) чашке весов, что и масса m.
Для описания всех таких разбиений сначала рассмотрим аналогичную задачу о взвешивании, в которой гири разрешается ставить только на одну чашу. В этом случае нам придется рассматривать такие разбиения целого числа M = m1 + m2 + ... + ms, в которых каждое целое число m от 0 до M представляется единственным образом в виде m = g1m1 + g2m2 + ... + gsms , причем каждое ai Î {0, 1}. (Повторяющиеся части mi по-прежнему считаются неразличимыми.) Такие разбиения числа M называются совершенными.
Теорема 1. [4] Количество совершенных разбиений числа M совпадает с количеством упорядоченных разложений числа M + 1 в произведение натуральных чисел без единичных множителей.
Доказательство. В каждом совершенном разбиении, очевидно, должна содержаться, по крайней мере, одна часть, равная 1. Предположим, что в нём содержится q1 - 1 частей, равных единице. Тогда все числа, меньшие q1, обладают только одним разбиением, и, значит, число q1 будет следующей частью совершенного разбиения. Пусть теперь в разбиении содержится q2 - 1 частей, равных q1, тогда все числа от 1 до q1 - 1 + q1(q2 - 1) = q1q2 - 1 единственным способом выражаются с помощью 1 и q1. Продолжая рассуждения аналогичным образом, приходим к совершенному разбиению вида
(1)
Сумма всех составных частей этого разбиения равна M, поэтому
M = q1 - 1 + q1(q2 - 1) + … + (q1q2 … qs – 1)(qs - 1) = q1q2 … qs – 1qs - 1,
и значит, qi являются делителями числа M + 1. Таким образом, упорядоченный набор чисел q1 , q2 , … , qs полностью определяет данное разбиение, при этом каждый сомножитель qi больше 1.
Теорема 2. Количество идеальных разбиений числа M совпадает с количеством совершенных разбиений числа 2M.
Доказательство. Пусть M = m1 + m2 + ... + ms — идеальное разбиение числа, то есть любое целое число m от 0 до M представляется единственным образом в виде m = a1m1 + a2m2 + ... + asms , где каждое ai Î {–1, 0, 1}. Тогда разбиение числа 2M = m1 + m1 + m2 + m2 + ... + ms + ms является совершенным. Действительно, если 0 £ m £ M, то число M - m также лежит в диапазоне от 0 до M, и по определению идеального разбиения M - m есть линейная комбинация слагаемых mi с коэффициентами ai Î {–1, 0, 1}. Тогда m = M - (M - m) = ∑ (1 - ai)mi , где 1 - ai Î {0, 1, 2}. Если же M £ m £ 2M, то число m - M находится в диапазоне от 0 до M и единственным способом представляется в виде линейной комбинации частей mi с коэффициентами ai Î {–1, 0, 1}. Тогда m = (m - M) + M будет линейной комбинацией тех же частей с коэффициентами 1 + ai Î {0, 1, 2}. Таким образом, любое целое число 0 до 2M представляется единственным образом в виде g1m1 + g2m2 + ... + gsms , причем gi Î {0, 1, 2}. Другими словами, части m1 , m1 , m2 , m2 , ... , ms , ms образуют совершенное разбиение числа 2M.
Докажем теперь, что каждому совершенному разбиению числа 2M соответствует некоторое идеальное разбиение числа M. Количество совершенных разбиений по теореме 1 совпадает с числом упорядоченных факторизаций числа 2M + 1, поэтому достаточно доказать соответствие между упорядоченными разложениями 2M + 1 на множители и идеальными разбиениями числа M. Пусть 2M + 1 = q1q2 … qs , и все сомножители в этом произведении больше 1. Кроме того, каждое qi – нечетное число, и значит, qi - 1 – четное число, не меньшее 2. По определению каждое целое m между 0 и 2M единственным образом представляется в виде линейной комбинации частей разбиения с коэффициентами ai Î {0, 1}. Так как qi - 1 – четные, то все части совершенного разбиения (1) числа 2M входят в это разбиение четное число раз. Уменьшив количество частей вдвое, мы получим разбиение числа M
, (2)
при этом любое целое m от 0 до 2M представляется в виде линейной комбинации этих частей с коэффициентами gi Î {0, 1, 2}. С помощью аналогичных рассуждений из первой части теоремы, мы получаем, что (2) дает идеальное разбиение числа M. Теорема доказана.
Приведенные выше идеальные разбиения для числа M = 40 соответствуют упорядоченным факторизациям числа 2M + 1 = 81 = 3 × 27 = 9 × 9 = 3 × 3 × 9 = 27 × 3 = 3 × 9 × 3 = 9 × 3 × 3 = 3 × 3 × 3 × 3.
Количество упорядоченных факторизаций. Пусть N > 1. Количество нетривиальных упорядоченных факторизаций числа 
зависит только от показателей n1 , n2 , … , ns , обозначим это количество через T(n1 , n2 , … , ns).
Теорема 3. Для функции 
справедлива рекуррентная формула
(3)
где сумма берётся по всем наборам, в которых 0 £ ki £ ni (1 £ i £ s) и k1 + k2 + … + ks < n1 + n2 + … + ns , причем 
.
Доказательство. Пусть 
– произвольный нетривиальный делитель числа N, отличный от N, то есть N = md и m > 1. Тогда всякая факторизация числа N, у которой первый множитель равен m, получается из соответствующей факторизации числа d, причём число последних, очевидно, равно T(k1 , k2 , … , ks). Отсюда следует равенство (3).
Формулы для подсчёта количества упорядоченных факторизаций сильно упрощаются в тех случаях, когда в каноническом разложении натурального N ³ 2 все простые множители входят только в первых степенях, то есть когда все ni равны 1. В формулировке следующей теоремы для набора n1 = n2 = … = ns = 1 используем обозначение 1s.
Теорема 4. Для натуральных чисел, разложения которых не содержат квадратов простых чисел, справедливо рекуррентное соотношение
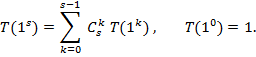(4)
Доказательство. Все делители числа N = p1 p2 … ps описываются наборами (k1, k2, ... , ks), где каждое ki равно 0 или 1. Очевидно, существует 
наборов, в которых все ki , кроме одного, равны 0; существует 
наборов, в которых все ki , кроме двух, равны 1, и т.д. Этим наборам соответствуют равные слагаемые в формуле (3), и значит, сумма в правой части (3) для каждого k содержит 
слагаемых, равных 
. Отсюда приходим к формуле (4).
Теорема 5. Количество упорядоченных факторизаций числа 
равно экспоненциальному числу Белла порядка 
, то есть
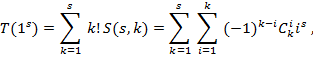(5)
где 
– число Стирлинга второго рода.
Пример 1. Пусть s = 3 и n1 = n2 = n3 = 1. По формуле (5) получаем
Пример 2. Пусть s = 4 и n1 = n2 = n3 = n4 = 1. По формуле (4)
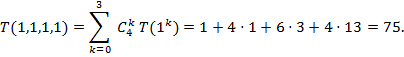
Отметим также связь специальных функций с числом упорядоченных факторизаций T(n1, n2), доказанную в статье [1].
Теорема 6. Количество упорядоченных факторизаций числа 
равно
где 
– многочлен Якоби степени n.
Следствие. Количество упорядоченных факторизаций числа 
равно
где Pn(x) – многочлен Лежандра степени n.
Общая формула для подсчета числа упорядоченных факторизаций с помощью комбинаторных рассуждений была получена П. Мак-Магоном [5]. Другая, более сложная вычислительная формула, установлена также в работе [3]. Иной подход к определению количества совершенных разбиений предложен в работе [2], в которой получены новые рекуррентные формулы для функции T. С помощью этих соотношений вычисление числа разбиений сводится к задаче нахождения количества разбиений числа N на части, каждая из которых не меньше 2. Для вычисления этого количества требуется подсчитать число разбиений на части, не меньшие 3 и т. д.
Рецензенты:
Елизаров А. М., доктор физико-математических наук, профессор, зам. директора по научной деятельности, Казанский (Приволжский) федеральный университет, г. Казань.
Игнатьев Ю. Г., доктор физико-математических наук, профессор, зав. кафедрой высшей математики и математического моделирования, Казанский (Приволжский) федеральный университет, г. Казань.
Антонов Александр Владимирович, д.т.н., профессор, декан факультета "Кибернетики", Обнинский институт атомной энергетики Национального исследовательского ядерного университета МИФИ Министерства образования и науки РФ, г. Обнинск.