Введение
В настоящее время наметилась тенденция разработки и исследования так называемых неортогональных механизмов, типичными представителями которых являются: двухзвенный механизм [1], поворотный стол с поворотной платформой [3], пространственный манипулятор с гибкими нитями [2], «NIST Robocrane» [4], манипуляторы с параллельной кинематической структурой [5] и многие другие. Как показали исследования, ошибка интерполяции линейной траектории движения рабочего инструмента для таких механизмов в значительной степени зависит от расположения интерполируемого отрезка прямой в пределах зоны обслуживания. Таким образом, разработка методики оценки ошибки интерполяции для неортогональных механизмов является весьма актуальной задачей.
Цель исследования
Разработка способа оценки ошибки интерполяции линейной траектории движения рабочего инструмента для неортогональных механизмов.
Материалы и методы исследования
При проведении исследований использовались методы аналитической геометрии, а также методы численного решения систем нелинейных уравнений.
Результаты исследования и их обсуждение
В данной работе предлагается способ исследования ошибки интерполяции линейной траектории перемещения рабочего инструмента неортогонального манипулятора с гибкими нитями, представляющий собой четыре вертикальные колонны (см. рисунок 1), установленные в точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() в которых укреплены первые концы невесомых и нерастяжимых нитей, вторые концы нитей соединяются в точке
в которых укреплены первые концы невесомых и нерастяжимых нитей, вторые концы нитей соединяются в точке ![]() , перемещающиеся в пространстве по заданной траектории. Перемещение рабочего инструмента (схвата, покрасочной головки или другого), закрепленного в точке
, перемещающиеся в пространстве по заданной траектории. Перемещение рабочего инструмента (схвата, покрасочной головки или другого), закрепленного в точке ![]() , возможно только с помощью изменения длин нитей
, возможно только с помощью изменения длин нитей ![]() ,
, ![]() ,
, ![]() ,
, ![]() по определенному закону. Изменение длин нитей осуществляется посредством их намотки (смотки) на барабаны (Б) диаметром
по определенному закону. Изменение длин нитей осуществляется посредством их намотки (смотки) на барабаны (Б) диаметром ![]() , приводимых во вращение с помощью приводов (П), установленных в основании вертикальных колон.
, приводимых во вращение с помощью приводов (П), установленных в основании вертикальных колон.
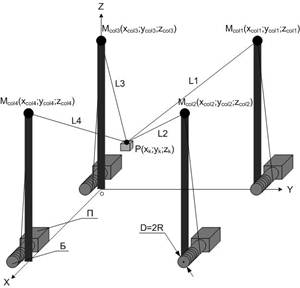
Рисунок 1. Пространственный манипулятор
Решение обратной кинематической задачи было получено в [ссылка] и может быть представлено в следующем виде:
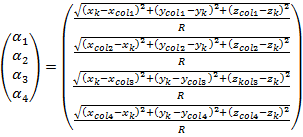 (1)
(1)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - обобщенные координаты, представленные в виде углов поворота барабанов,
- обобщенные координаты, представленные в виде углов поворота барабанов, ![]() ,
, ![]() ,
, ![]() - заданные координаты рабочего инструмента.
- заданные координаты рабочего инструмента.
Так как приводы (П) физически не способны обеспечить расчетное значение углов ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то допустим, что углы поворота барабанов могут изменяться дискретно с шагом
, то допустим, что углы поворота барабанов могут изменяться дискретно с шагом ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда
, тогда
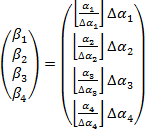 (2)
(2)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - дискретные углы поворота барабанов,
- дискретные углы поворота барабанов, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - целое число шагов приводов.
- целое число шагов приводов.
Решение прямой кинематической задачи с учетом (2) запишем в виде системы уравнений:
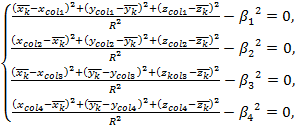 (3)
(3)
где ![]() ,
, ![]() ,
, ![]() - декартовы координаты рабочего инструмента, полученные в результате решения прямой задачи кинематики с учетом дискретности улов поворота барабанов, причем
- декартовы координаты рабочего инструмента, полученные в результате решения прямой задачи кинематики с учетом дискретности улов поворота барабанов, причем ![]() ,
, ![]() и
и ![]() . Таким образом, вектор
. Таким образом, вектор
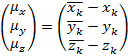 (4)
(4)
представляет собой ошибку позиционирования рабочего инструмента по каждой декартовой координате с учетом дискретности шага приводов. В том случае, когда осуществляется линейная интерполяция отрезка прямой, заданного двумя точками ![]() и
и ![]() (см. рисунок 2), координаты промежуточных точек
(см. рисунок 2), координаты промежуточных точек ![]() ,
, ![]() , лежащих на этом отрезке, могут быть найдены из соотношения:
, лежащих на этом отрезке, могут быть найдены из соотношения:
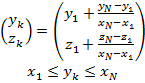 (5)
(5)
Решив обратную задачу кинематики пространственного манипулятора, а затем прямую задачу с учетом дискретности поворота барабанов в каждой точке, лежащей на заданном отрезке ![]() , получим точки
, получим точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() , координаты которых будут отличаться от заданных на величину позиционной ошибки, определяемой выражением (4).
, координаты которых будут отличаться от заданных на величину позиционной ошибки, определяемой выражением (4).
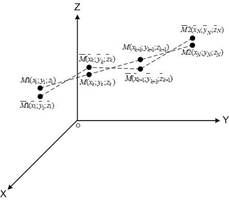
Рисунок 2. Результат интерполяции заданного отрезка прямой ![]() с некоторой ошибкой
с некоторой ошибкой
Для анализа ошибки линейной интерполяции в данной работе будут использоваться следующие статистические характеристики: дисперсия ошибки, которая для случая интерполяции одного отрезка прямой может быть определена из (6); среднеквадратическое отклонение ошибки можно определить из известного соотношения (7); максимальное значение ошибки интерполяции на интервале – (8).
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Следует отметить, что при анализе статистических характеристик ошибки линейной интерполяции, точки ![]() ,
, ![]() должны лежать в одной плоскости, ортогональной заданному отрезку прямой
должны лежать в одной плоскости, ортогональной заданному отрезку прямой ![]() .
.
Для исследования статистических характеристик ошибки линейной интерполяции траектории перемещения рабочего инструмента пространственного манипулятора в пределах всей его зоны обслуживания, ограниченной вертикальными колонами, в данной работе предлагается способ формирования семейства отрезков прямых, сущность которого поясняет рисунок 3.
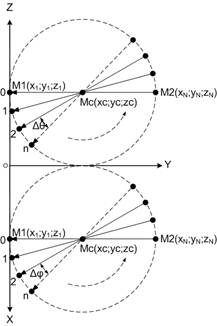
Рисунок 3. Способ формирования семейства отрезков прямых в зоне обслуживания пространственного манипулятора
Семейство отрезков прямых формируется путем поворота исходного отрезка прямой ![]() (вращение осуществляется относительно оси в точке
(вращение осуществляется относительно оси в точке ![]() , расположенной посередине отрезка
, расположенной посередине отрезка ![]() ) на угол
) на угол ![]() в плоскости
в плоскости ![]() и на угол
и на угол ![]() в плоскости
в плоскости ![]() . Целое число
. Целое число ![]() определяет номер прямой, полученной в результате поворота отрезка прямой
определяет номер прямой, полученной в результате поворота отрезка прямой ![]() на некоторый угол. Диапазон изменения углов:
на некоторый угол. Диапазон изменения углов: ![]() и
и ![]() . В результате координаты начала и конца отрезка прямой
. В результате координаты начала и конца отрезка прямой ![]() при всех возможных комбинациях
при всех возможных комбинациях ![]() и
и ![]() образуют в рабочей зоне пространственного манипулятора сферу, радиус которой равен половине длинны отрезка
образуют в рабочей зоне пространственного манипулятора сферу, радиус которой равен половине длинны отрезка ![]() . Зависимость координат точки
. Зависимость координат точки ![]() от углов
от углов ![]() и
и ![]() может быть представлена в виде:
может быть представлена в виде:
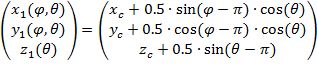 (9)
(9)
По аналогии, зависимость координат точки ![]() от улов
от улов ![]() и
и ![]() :
:
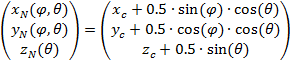 (10)
(10)
Таким образом, можно определить статистические характеристики ошибки линейной интерполяции для каждой прямой из сформированного семейства в виде функций:
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
где ![]() - точка, лежащая на заданном отрезке прямой с началом в точке
- точка, лежащая на заданном отрезке прямой с началом в точке ![]() и концом в точке
и концом в точке ![]() ,
, ![]() - точка, координаты которой получены в результате линейной интерполяции отрезка
- точка, координаты которой получены в результате линейной интерполяции отрезка ![]() .
.
С использованием пакета MATLAB разработана компьютерная модель, которая позволяет анализировать статистические характеристики ошибки интерполяции траекторий перемещения рабочего инструмента пространственного манипулятора в пределах всей зоны обслуживания и представлять результаты моделирования графически. На рисунках 4, 5 графически представлены функции ![]() и
и ![]() соответственно. Графики были получены при следующих значениях входных параметров компьютерной модели:
соответственно. Графики были получены при следующих значениях входных параметров компьютерной модели: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
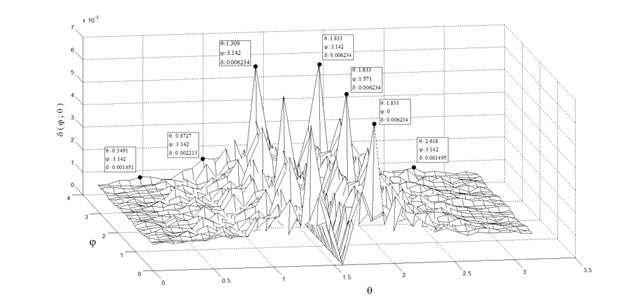
Рисунок 4. Зависимость максимальной ошибки интерполяции отрезка прямой от улов его поворота в пространстве
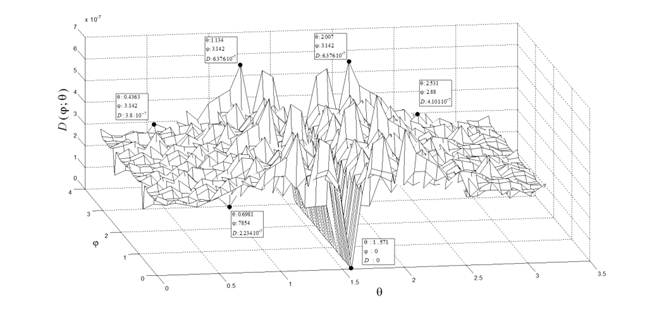
Рисунок 5. Зависимость дисперсии ошибки интерполяции отрезка прямой от улов его поворота в пространстве
Выводы
Таким образом, проведенные исследования позволили определить локальные зоны с ярко выраженными перепадами значений ошибки, например, на графике зависимости максимальной ошибки интерполяции отрезка прямой от углов его поворота в пространстве (рисунок 4) можно выделить ряд экстремумов функции ![]() , которая принимает максимальное значение
, которая принимает максимальное значение ![]() при следующих значениях углов
при следующих значениях углов ![]() и
и ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . При
. При ![]() и
и ![]() ,
, ![]() , что соответствует циклу подъема рабочего инструмента по линейной траектории, проходящей через центр плоскости
, что соответствует циклу подъема рабочего инструмента по линейной траектории, проходящей через центр плоскости ![]() .
.
Аналогичный подход для оценки ошибки линейной интерполяции может быть применен и к другим неортогональным механизмам осуществляющим перемещение рабочего инструмента как на плоскости, так и в пространстве.
Работа выполнена в рамках федеральной целевой программы ФЦП "Научные и научно-педагогические кадры инновационной России" на 2009-2013 годы.
Рецензенты:
Адигамов Касьян Абдурохманович, доктор технических наук, профессор, заведующий кафедрой «Прикладная механика и конструирование машин» ФГБОУ ВПО «Южно-Российского государственного университета экономики и сервиса», г.Шахты.
Абезин Валентин Германович, доктор технических наук, профессор кафедры «Сельскохозяйственные машины» ФГБОУ ВПО «Волгоградского государственного аграрного университета», г.Волгоград.



