В литературе, посвященной проблемам управления, существует множество разнообразных концепций и подходов к определению управления. В предлагаемых концепциях управления промышленным предприятием вопрос информационной области остается открытым, поскольку научная разработанность теоретических и методологических положений определения информационной концепции для целей управления предприятием является недостаточной. Многие исследователи проблем информационного обеспечения системы управления промышленным предприятием обращаются к вопросам организации системы бухгалтерского управленческого учета, игнорируя другие учетные системы. С практической точки зрения, функциональные компоненты информационной области управления промышленным предприятием (бухгалтерская финансовая информационная система, бухгалтерская управленческая информационная система, бухгалтерская налоговая информационная система) не способны в полном объеме удовлетворять информационные потребности системы управления. То есть ни аппаратно, ни организационно не взаимодействует с информационными системами управления технологическими процессами.
Создание информационной системы управления технологическим процессом возможно только при условии наличия автоматизированных систем управления технологическим процессом (АСУТП). Любая информационная система ориентирована на работу в конкретной предметной области. При построении интегрированной информационной системы необходимо учитывать и различать следующие понятия: объект исследования, модель объекта, составная модель данных, элементарная модель данных, информационная основа. Объектом исследования будет являться любой из объектов предметной области – всё то, что может храниться в базе данных ИИС. При исследовании объектов окружающей действительности осуществляется сбор данных, часто разрозненных и неоднородных из которых необходимо формировать модели объектов. Первичные данные – исходные данные, получаемые в ходе непосредственного сбора информации. После сбора разнообразные входные данные об объектах упрощаются, унифицируются и преобразуются в модели, хранимые в базе данных.
Основной задачей эксплуатации промышленных предприятий является поддержание их технического состояния и надежности на уровне, достаточном для выполнения ими заданных функций, что позволяет выдерживать приемлемые экономические показатели.
С появлением современной микропроцессорной техники стала возможной автоматизация сбора данных об отказах и восстановлениях используемого технологического оборудования и отдельных агрегатов. Полученные данные можно использовать для построения ряда математических моделей, необходимых для исследования системы эксплуатации с целью получения их максимальной эффективности использования:
1) модель динамики изменения надежности системы в процессе эксплуатации;
2) модель оптимального обслуживания;
3) модель оценки количества запасных элементов;
4) модель оценки эффективности затрат на восстановление и ремонт.
Основополагающими параметрами, необходимыми для построения математических моделей, являются интенсивности отказов λi и восстановлений μi, т.е. исходные данные, получаемые непосредственно с контроллеров, составляющих основу АСУ ТП. Достоверность данных и адекватность вышеперечисленных математических моделей проверялась на основе наблюдений, организованных на КДК СМК-350 (ОАО «МЗКСМ», ст. Мстера Владимирской области) в течение 12 лет (в 2000-2012 гг.) и продолжающихся до сих пор. КДК СМК-350 был разработан и выполнен по инжиниринговому проекту фирмы UNIMORANDO (Италия) с использованием контроллеров S5-210В (SIEMENS, Германия). Однако в процессе эксплуатации возникла необходимость в реконструкции системы управления с целью замены устаревших узлов и агрегатов технологического оборудования и АСУТП, а также дополнении системы устройствами сбора, обработки, хранения и передачи информации о надежности КДК по параметрам производительности и качества. Непрерывный технологический процесс (ТП) производства кирпича на КДК СМК-350 состоит из операций формовки, сушки, садки и обжига, которым соответствуют технологические участки и отделения. На рис. 1 представлена технологическая схема КДК СМК-350, в которой обозначены связи отдельных технологических участков и отделений.
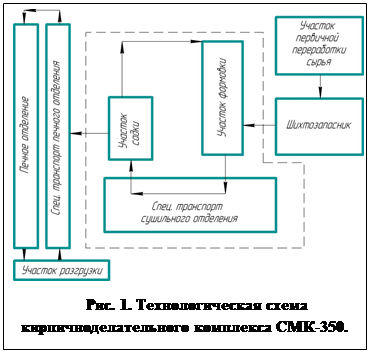
Анализ ТП и технологической схемы на рис. 1 позволяет однозначно определить ТС КДК СМК-350 как двухучастковую систему с промежуточным накопителем. В качестве накопителя выступает сушильное отделение вместе со своим спецтранспортом.
Для описания модели надежности ТС (модель 1) использовался математический аппарат Марковских случайных процессов с дискретными состояниями и непрерывным временем, т.к. все возможные состояния системы S1… Sn можно заранее перечислить (табл. 1). В модели задавались потоки отказов и восстановлений, для которых находились вероятности нахождения системы в работоспособном состоянии. Математическая модель надежности ТС с НЦ имеет восемь возможных состояний Si и представляет собой систему дифференциальных уравнений Колмогорова:
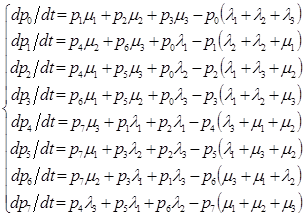 (1)
(1)
где t – время, а р0…р7 вероятности нахождения системы в одном из состояний, λi и μi интенсивности отказов и восстановлений каждого из трех участков (формовки, сушки и садки).
Таблица 1 – Возможные состояния системы из трех элементов
|
Состояние |
Элемент ТС с НЦ |
Примечания |
||
|
1 |
2 |
3 |
||
|
S0 |
р |
Р |
р |
работоспособны все три элемента |
|
S1 |
н |
Р |
р |
неработоспособен 1-й элемент |
|
S2 |
р |
Н |
р |
неработоспособен 2-й элемент |
|
S3 |
р |
Р |
н |
неработоспособен 3-й элемент |
|
S4 |
н |
Н |
р |
неработоспособны 1-й и 2-й элементы |
|
S5 |
р |
Н |
н |
неработоспособны 2-й и 3-й элементы |
|
S6 |
н |
Р |
н |
неработоспособны 1-й и 3-й элементы |
|
S7 |
н |
Н |
н |
все три элемента неработоспособны |
н – неработоспособен,
р – работоспособен.
Создание модели оптимального обслуживания (модель 2) необходимо для определения продолжительности работы системы Тп до очередного технического обслуживания (ТО). Требования к надежности ТС задаются в виде вероятности pтр нахождения ее в технически исправном состоянии к началу очередного ТО. По статистическим данным эксплуатации оценивается вид функции λ(t). Вероятность нахождения системы в технически исправном состоянии за время t1+Тп может быть представлена в виде:
 ,
,
где t1 – время эксплуатации системы до рассматриваемого момента времени.
В результате преобразований получаем уравнение, из которого может быть определен требуемый период Тn :
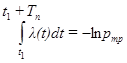 .
.
В случае λ(t)=a+bt, когда поведение системы описывается Марковским неоднородным процессом с дискретными состояниями и непрерывным временем, получаем уравнение в виде:
![]() . (2)
. (2)
По статистическим данным определяются и уточняются параметры a и b, по формуле (2) определяется очередной период Тп. После очередного технического обслуживания расчеты повторяются.
Модель оценки количества запасных элементов (модель 3) построена на основе задачи целочисленного нелинейного программирования. Формулировка задачи: технологическая система состоит из элементов k типов, характеристики надежности которых известны. Для увеличения надежности мы придаем некоторое число n1 резервных элементов первого типа, n2 – второго типа, n3 – третьего типа, nk – к-го типа. Спрашивается, как нужно выбрать числа n1, n2,… nk при заданном числе рабочих элементов каждого типа, чтобы вероятности безотказной работы в промежутке времени от 0 до t была максимальна.
K(t)=k(t;n1,n2,n3,…nk)
При этом на величины n1,n2,n3,…nk накладываются дополнительные условия:
![]()
Двухучастковая система с промежуточным накопителем состоит из трех элементов; к=3;
k1 – формовка; n1 – список быстроизнашивающихся деталей этого участка;
k 2 – садка; n2 – список быстроизнашивающихся деталей этого участка;
k 2 – СТС; n3 – список быстроизнашивающихся деталей этого участка;
Наложены ограничения по стоимости (стоимость каждой детали известна).
Условия ограничения по стоимости:
![]() (1)
(1)
Максимизируется вероятность безотказной работы. Вероятность безотказной работы каждой детали из списка должна быть известна, если неизвестна, то определяется как 1-Q(t) – единица минус вероятность отказа, либо из выражения:
![]()
Найти неотрицательные значения n, которые удовлетворяют равенству (1), т.е. найти количество деталей, с помощью которых можно поддерживать необходимый уровень надежности.
Модель оценки эффективности затрат на восстановление и ремонт (модель 4) может быть выражена уравнением:
![]() , (3)
, (3)
где W0 – вероятность выполнения задания ТС с НЦ, po – обобщенный показатель надежности, α – параметр, определяемый по статистическим данным.
Расчет вероятности W0 выполнения задания для случая, когда номинальная производительность ТС определяется номинальной производительностью второго участка, производим по формуле:
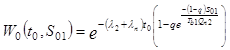 ,
,
где ![]()
![]()
В качестве исходной информации для исследования модели используются следующие параметры и статистические данные: λi – интенсивности отказов участков ТС, Qn – номинальные производительности участков ТС, λni – интенсивности отказов межоперационных накопителей, Soi – уровни начального заполнения накопителей, Tbi – средние времена восстановления накопителей, Si – емкость i-го накопителя, Tni – средние времена восстановления накопителей.
Стоимость эксплуатации ТС с НЦ С1 и ее обобщенный показатель надежности pо связаны между собой математической зависимостью:
![]() (4)
(4)
Из (3) и (4) получим: ![]() , (5)
, (5)
где ![]() относительная стоимость эксплуатации одной системы при надежности p0:
относительная стоимость эксплуатации одной системы при надежности p0:
![]()
Финальные вероятности состояний ТС с НЦ получаются путем решения системы алгебраических уравнений, которые получаются из (1). Если система такова, что отказ на любом этапе приводит к одним и тем же последствиям (не выполнению задачи) и при этом «стоимость» отказа (потери, вызванные появлением отказов) на всех этапах одинакова, то определение оптимальных значений основных показателей надежности производим по формуле:
![]()
где p0 – значение обобщенного показателя надежности системы. Кг – коэффициент готовности системы, p(τп) – вероятность исправности во время подготовки системы, p(τпр) – вероятность исправности во время применения [4].
Если стоимость отказов на разных этапах разная, то для строгого решения задачи целесообразно показатели экономичности системы определять непосредственно через основные показатели ее надежности с последующим поиском оптимальных решений по каждому показателю надежности.
Следовательно, имея статистические данные о значениях W0 и p0, можно вычислить значение α по формуле (5) и относительную стоимость эксплуатации одной системы при заданной надежности p0. Полученные показатели будут являться базовыми. Их можно использовать при расчете модернизируемой системы как систему-аналог. Величина α зависит от способа повышения надежности системы. Наименее экономичным является способ дублирования всех элементов, отказ которых приводит к отказу системы (![]() ).
).
Таким образом, взаимосвязь бухгалтерской финансовой и бухгалтерской управленческой информационных систем с информационной системой управления технологическим процессом может быть осуществлена посредством предоставления ими информации для решения математических моделей оценки количества запасных элементов и оценки эффективности затрат на восстановление и ремонт, что позволяет в дальнейшем автоматизировать управление складскими запасами. Также данная взаимосвязь предполагает устранить искусственное разделение автоматизированных систем предприятий на АСУ, САПР и АСУТП. Структурная схема ИИС предприятия представлена на рисунке 2.
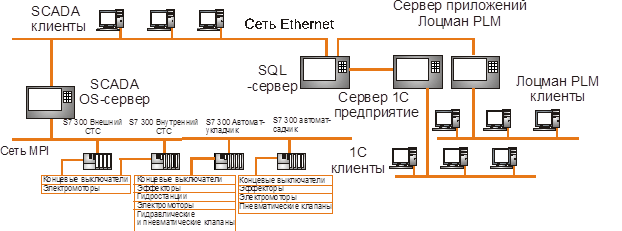
Рис. 2. Структурная схема интегрированной информационной системы предприятия.
Описание и расчет модели данной системы при различных исходных данных производится на языке для технических расчетов MatLab. В итоге на предприятии должна возникнуть корпоративная (комплексная) автоматизированная и математически описанная информационная система. В таких системах предусмотрены хранение, обработка и передача информации в компьютерных средах, оперативный доступ к данным в нужное время и в нужном месте.
Рецензенты:
Гоц А.Н., д.т.н., профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Кульчицкий А.Р., д.т.н., профессор, заместитель главного конструктора по испытаниям ООО «Владимирский моторо-тракторный завод», г. Владимир.



