Введение
Долгосрочное подтопление сельскохозяйственных территорий юга Украины, вызванное как природными (атмосферные осадки), так и антропогенными факторами (строительство каскада днепровских водохранилищ, систем каналов), приводит к значительным материальным и социальным убыткам. Поэтому задача прогнозирования изменения площадей с уровнем грунтовых вод требует разработки соответствующей методики, в основе которой будут лежать многолетние наблюдения за гидрогеологическим режимом почв в системе эколого-мелиоративного мониторинга.
Методология и методы исследований
Для реализации задачи ситуационного прогнозирования процессов подтопления сельскохозяйственных угодий нами предлагается создание прогнозной системной макромодели [3], которая базируется на построении дискретной цепи Маркова, как инструментария прогнозирования на основе анализа взаимодействия нескольких подсистем. На нижнем уровне иерархии рассматриваются модели подсистем: “Начальное положение уровня грунтовых вод”, “Уровень влажности грунта”, “Прогнозируемое количество осадков”, “Прогнозируемая водоподача” [4].
Подсистема “Начальный положение уровня грунтовых вод” классифицирует положение уровней грунтовых вод в данный момент времени множеством альтернатив: S=(S1,S2,S3,S4)=(“хороший”, “удовлетворительный”, “опасный”, “очень опасный”), каждая из которых описывает состояние реальной системы на определенной территории по данным наблюдений гидрогеолого-мелиоративной экспедиции за уровнем грунтовых вод.
Подсистема “Уровень влажности грунта” классифицирует состояние влажности грунта множеством альтернатив: M=(M1,M2,M3)=(“низкий”, “средний”, “высокий”), которая характеризует уровень влажности пласта грунта к уровню грунтовых вод из условия возможностей поглощения влаги, которая может поступать с осадками или поливами.
Подсистема “Прогнозируемое количество осадков” разрабатывается для классификации прогнозируемых метеорологических условий. Множество альтернатив прогнозируемых осадков может быть изображено вектором K=(K1,K2,K3)=(“незначительные”, “опасные”, “очень опасные”).
Подсистема “Прогнозируема водоподача” является фактором управления в задаче мониторинга и состоит из альтернатив: R=(R1,R2,R3)=(“незначительная”, “средняя”, “повышенная”), что отображают как экономические возможности поливов, так и экологические ограничения при принятии решений.
Алгоритм принятия решений в системе, т.е. алгоритм координации работы подсистем, характеризуется дискретной цепью Маркова, которая описывает вероятности переходов состояний уровней грунтовых вод ![]() .
.
Тогда, если величины ![]() характеризуют вероятность нахождения системы в момент времени
характеризуют вероятность нахождения системы в момент времени ![]() в состоянии
в состоянии ![]() , то вероятности
, то вероятности ![]() нахождения системы в состоянии
нахождения системы в состоянии ![]() в момент времени t+1 определяются матричным уравнением (рис. 1):
в момент времени t+1 определяются матричным уравнением (рис. 1):
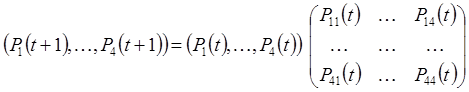 (1)
(1)
где ![]() рассматривается как вероятность перехода из состояния
рассматривается как вероятность перехода из состояния ![]() в состояние
в состояние ![]() .
.
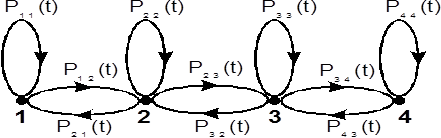
Рисунок 1. График вероятностей перехода Рij(t) цепи Маркова
Неопределенность в системе обусловлена неопределенностью начальных состояний ![]() , которое связано с недостаточной репрезентативностью наблюдательных буровых скважин.
, которое связано с недостаточной репрезентативностью наблюдательных буровых скважин.
Вторым источником неопределенности и риска при прогнозировании уровней грунтовых вод выступает неопределенность вероятностей перехода Pij(t), которые идентифицируются на основе совместного рассмотрения и анализа подсистем. Вероятности переходов определяются также на основе имитационного моделирования влагопереноса в грунтах относительно условий рассматриваемой зоны. Вероятностный прогноз с помощью уравнения (1) зависит от состояния системы в момент t и от метеорологических факторов (осадков, испарение) и регулирующего фактора – водоподача на орошении.
Макромодель дискретных цепей Маркова позволяет следить за состоянием водного режима и давать вероятностный прогноз экологически опасных ситуаций.
Пусть некоторая система (объект) может находиться в каждый момент времени t=0,1,... в одном из состояний, которые образовывают конечное множество х={1, …, N} с вероятностью Рі, і=1, ...п. Говорят, что поведение системы описывается однородной цепью Маркова с переходными вероятностями Ріj, если через единицу времени после того, как система находилась в состоянии і Î х, с вероятностью Ріj она переходит в состояние jÎх независимо от того, когда и которым путем она попала в состояние і. Если Ріj зависит от момента времени t, в который осуществляется переход, то говорят о неоднородной цепи Маркова. Матрицу Р=(Ріj) или Р(t)=(Ріj(t)) называют матрицей переходов или переходных вероятностей. Для однородных цепей Маркова, кроме вероятности начальных состояний, важную роль играют финальные вероятности состояний Рі*, вероятности пребывания в определенном состоянии при t ®φ [2].
Для решения задачи прогнозирования на основе цепей Маркова, пусть этапы системы отвечают некоторым физическим состояниям, связанным с экологической ситуацией, в частности с пребыванием системы в разных зонах риска. Тогда, например, четырем зонам риска („без рискованная зона”, „зона допустимого риска”, „зона критического риска”, „зона чрезвычайного риска”) отвечает цепь Маркова, которая состоит из четырех состояний Х={х1, х2, х3, х4}. Пребывание системы в каждом из состояний определяется определенной вероятностью, которая может быть рассчитана непосредственным измерением параметров, построением соответствующих шкал классификации состояний системы. При этом в каждый момент времени t находится вектор начальных состояний и матрица вероятностей перехода: Ріj (t) i, j = 1, ..., 4.
Задача системного прогнозирования заключается в построении системы прогнозирования S=S(x, å, V, F) на основе цепей Маркова, где x – состояния Марковской системы; å – структура системы и ее связи (вероятности перехода, связи с внешней средой å=å(V)); V – внешняя среда, которая влияет на алгоритм функционирования системы; F – функции, которые отображают алгоритм переходов системы (1) и функции выходов – вероятностные оценки пребывания системы в определенном состоянии и оценки соответствующих функций прибавок и потерь [5].
Рассмотрим определение вероятности начальных состояний Марковской системы на основе относительных оценок рисков. Пусть установленные статистические вероятности Рi состояния х4 („зона чрезвычайного риска”) в течение серии лет наблюдений. От абсолютных оценок рисков перейдем к относительным оценкам на основе отношения Pi/Pmax, где Pmax – максимальная вероятность зоны чрезвычайного риска для некоторого года наблюдений.
Относительные оценки позволяют построить ситуацию, которая отвечает одной из зон риска и разрешает лицу, которое принимает решение (ЛПР), разработать стратегию экономико-экологической деятельности по уровню возможных потерь. Создавая соответствующие шкалы риска (интервалы) для показателя Pi/Pmax, необходимо предусматривать не только начальные состояния цепи Маркова, что однозначно определяется попаданием отношения в определенный интервал, но и некоторые промежуточные начальные состояния, которые определяются определенными „промежуточными” интервалами, которые неоднозначно определяют вероятности пребывания системы.
Для классификации начальных состояний хi Марковской системы S используем шкалу относительных рисков Pi/Pmax, на основе которой начальные состояния определяются соотношениями [3]:
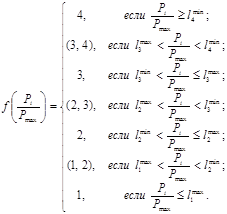 (2)
(2)
Если отношение Pi/Pmax попадает в интервал, который однозначно определяет состояние системы Si, то начальная вероятность данного состояния ![]() =1. Началу вероятности нахождения системы Si в одном из промежуточных состояний (k, j) определяются “близостью” к каждому из промежуточных состояний по формулам [4]:
=1. Началу вероятности нахождения системы Si в одном из промежуточных состояний (k, j) определяются “близостью” к каждому из промежуточных состояний по формулам [4]:
в k-м состоянии:
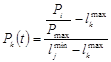 ; (3)
; (3)
в j-м состоянии:
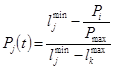 . (4)
. (4)
Рассмотрим идентификацию структуры системы и вероятностей перехода. Вероятности перехода Ріj (t) в каждый момент времени t в сложных системах могут существенно зависеть от внешней среды V=V(И, q). Т.е. от управленческих действий ЛПР, что характеризуются величиной И, и от стохастичных влияний природы q в данный момент времени, т.е. структура системы å является функцией внешней среды å=å (V). При этом осуществляется классификация внешних влияний (построение ситуаций φ) по распределению V (И, q) на подмножества [5]:
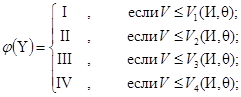 (5)
(5)
причем:
![]() (6)
(6)
В соответствии с ситуацией φ, которая определяется внешним влиянием V(И, q), для прогнозирования экологического процесса используются соответствующие прогностические системы åк – цепи Маркова, которые описываются соответствующими ситуациями φ вероятностями перехода Ріjк (t), і, j Î [1, 4]:
å=åк, если V (И, q) £ Vк (И, q), К=1, ... Кі (7)
Идентификация вероятностей перехода Ріjк(t) в модели прогнозирования для конкретного объекта осуществляется относительно заданной ситуации φ на основе статистических оценок данных в прошлом или экспертных оценок, полученных на основе многолетних наблюдений данного объекта или объектов-аналогов.
Для идентификации цепи Маркова åк относительно ситуации φ используют ряд гистограмм площадей распределения за годы наблюдений [1] и соответствующие им диаграммы осадков и поливов. Для этого определяются на множестве гистограмм для каждого года состояния системы по формулам (2–4). Для каждого года наблюдений и определенных соответствующих состояний системы, на основе прогнозируемых суммы осадков и поливов (как прогнозные принимаются сумма осадков и поливов следующего года наблюдений), определяются ситуации φ (т.е. четыре ситуации типа 5). Таким образом, множество наблюдений распадается на четыре подмножества, каждое из которых используется для идентификации соответствующей цепи Маркова åк относительно ситуации φ. При наличии значительного ряда наблюдений в соответствующем подмножестве определяются частоты переходов из определенного состояния в другое, как вероятности перехода Ріjк(t). В тех случаях, когда недостаточно статистических данных, используются, на основе понятных принципиальных зависимостей, экспертные оценки вероятностей перехода системы из каждого данного состояния в другие состояния [5].
Для решения задачи прогнозирования потерь чистой прибыли от недополучения урожая в результате подтопления сельскохозяйственных территорий используются данные прогноза изменения площадей с уровнем грунтовых вод, сгруппированные по зонам риска (Х={х1, х2, х3, х4}), выполненные при помощи аппарата цепей Маркова, а также вычисленные экспертом весовые коэффициенты (R={r1, r2, r3, r4}), учитывающие снижение урожая сельскохозяйственных культур, при выращивании их на территориях приуроченных к разным зонам риска (полученные на основании анализа многолетних статистических данных для данной территории). Для перехода от относительных оценок недополученного урожая сельскохозяйственных культур к абсолютным (денежные единицы) предложено использовать данные о средневзвешенной чистой прибыли от сельскохозяйственного производства для данного района на текущий момент времени Р.
Таким образом, прогноз потерь чистой прибыли от недополучения урожая в результате подтопления сельскохозяйственных территорий определяется по формуле:
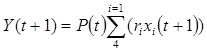 (8)
(8)
где ![]() – прогноз потерь чистой прибыли от недополучения урожая в результате подтопления сельскохозяйственных территорий;
– прогноз потерь чистой прибыли от недополучения урожая в результате подтопления сельскохозяйственных территорий;
![]() – средневзвешенная чистая прибыль от сельскохозяйственного производства для данного района на текущий момент времени;
– средневзвешенная чистая прибыль от сельскохозяйственного производства для данного района на текущий момент времени;
![]() – прогноз изменения площадей с уровнем грунтовых вод, сгруппированных по зонам риска;
– прогноз изменения площадей с уровнем грунтовых вод, сгруппированных по зонам риска;
![]() – весовые коэффициенты, учитывающие снижение урожая сельскохозяйственных культур для каждой зоны риска.
– весовые коэффициенты, учитывающие снижение урожая сельскохозяйственных культур для каждой зоны риска.
Выводы
Методические положения, изложенные ранее, позволяют на своей основе разработать систему анализа и прогноза динамики площадей с уровнем грунтовых вод с последующим картографированием полученного материала, а также количественно определить величину убытков от недополучения урожая вследствие подтопления территории.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 2-05-90911-мол_снг_нр.
Рецензенты:
Лисецкий Ф. Н., д.г.н., профессор кафедры природопользования и земельного кадастра геолого-географического факультета ФГАУ ВПО Белгородский государственный национальный исследовательский университет, г. Белгород.
Корнилов А. Г., д.г.н., профессор, заведующий кафедрой географии и геоэкологии ФГАУ ВПО Белгородский государственный национальный исследовательский университет, г. Белгород.



