Рассмотрим задачу синтеза системы управления с несколькими целями управления.
Задана система обыкновенных дифференциальных уравнений, описывающая модель объекта управления
, (1)
где 
, 
, 
– ограниченное замкнутое множество, 
.
Состояние объекта управления оцениваем по наблюдаемым координатам
, (2)
где 
, 
.
Для системы (1) заданы начальные условия
, (3)
Задано множество целевых состояний
, (4)
причем 
.
Задан критерий качества управления
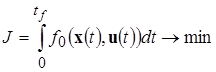, (5)
где 
– время управления, которое может быть ограничено, 
, но не задано.
Необходимо найти управление в форме
, (6)
которое обеспечивает достижение последовательно всех целевых точек (4) и минимизирует функционал (5).
Цель управления (4) многозначна. Для перехода к задаче синтеза интеллектуальной системы управления необходимо обеспечить в системе возможность выбора. Для этой цели ослабим требования к попаданию объекта в каждую целевую точку, заменим требованием попадания в окрестность целевой точки.
,
, (7)
где 
– малая положительная величина.
Тогда у нас появляется компромисс между точностью и скоростью достижения целевых точек. Для реализаций управления в данной задаче нам необходимо каждый раз решать задачу выбора между точным достижением текущей цели и переходом на другую цель. Очевидно, что при таком условии в системе управления помимо регулятора обратной связи, обеспечивающего достижение цели, необходимо иметь логический блок, осуществляющий переключение целей.
Уточним данную постановку задачи.
Управление (6) представим в виде функции, зависящей от расстояния до цели
(8)
где 
– номер текущей целевой точки.
В любой момент времени 
номер текущей целевой точки определяем с помощью логической функции
, 
, (9)
где 
, 
, 
- предикатная функция, 
: 
. (10)
Функцию (10) также необходимо найти вместе с синтезирующей функцией (6). Функция (10) должна обеспечивать переключение целевых точек. Обе функции (6) и (10) должны обеспечивать минимум функционалу качества (5) функционалу точности
, (11)
Время управления определяем по достижению последней целевой точки
, если 
, (12)
где 
– малая положительная величина.
Частный критерий (5) заменим суммарным критерием качества
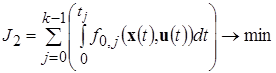(13)
Для построения предикатной функции используем функцию дискретизации и логическую функцию.
, (14)
где 
– логическая функция,
: 
, (15)
где 
, 
, 
– функция дискретизации.
Задача заключается в том, чтобы найти управления в форме
, (16)
где 
– целочисленный вектор, определяющий управления для решения частной задачи 
. Управления (16) должно обеспечить достижения минимумов функционалов (11) и (13).
В общем случае, так как задача содержит два критерия (11) и (13), то ее решением будет множество Парето в пространстве функционалов 
. Конкретное решение на множество Парето выбирает разработчик по результатам моделирования и исследования синтезированной системы управления.
Задачу (1) – (3), (7) – (16) называем задачей синтеза интеллектуальной системы управления. Для ее решения необходимо найти две многомерные синтезирующие функции 
и 
.
Для решения задачи синтеза интеллектуальной системы управления используем метод сетевого оператора [1–7]. Для нахождения функции используем обычный арифметический сетевой оператор, в котором в качестве конструктивных функций используем множество арифметических функций с одним или двумя аргументами. В методе сетевого оператора эти функции называются унарными или бинарными операциями. Для нахождения логической функции используем логический сетевой оператор, соответственно с унарными и бинарными логическими операциями.
В качестве примера рассмотрим следующую математическую модель
,
,
где 
, 
– координаты на плоскости.
На управление наложены ограничения 
Траектория движения задана набором точек
.
Необходимо найти управление, чтобы минимизировать две целевые функции объекта. Первый функционал определяет точность движения по траектории, а второй – время прохождения траектории.
,
,
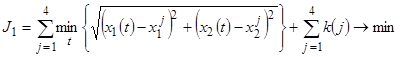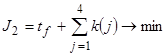где
, 
,
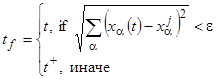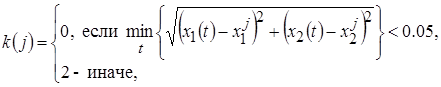
Задача логического управления заключалась в обеспечении переключения точек траектории.
,
где 
, 
, 
,
, 
.
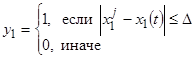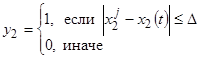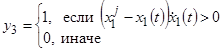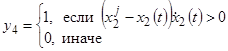Начальные значения для моделирования были 
.
На рис. 1 приведено полученное решение в виде множества Парето.
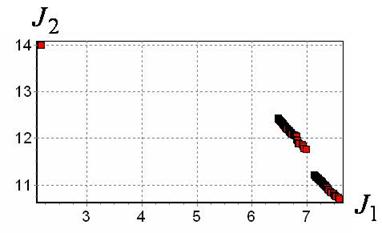
Рис. 1. Множество Парето
На множестве Парето было отобрано лучшее решение по критерию 
. Полученные матрицы арифметического и логического сетевых операторов имеют следующий вид
, 
.
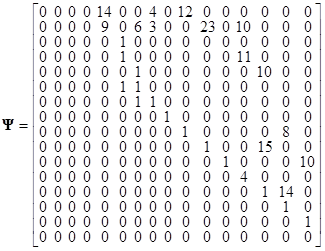На рис. 2,3 показаны результаты моделирования отобранной системы управления.
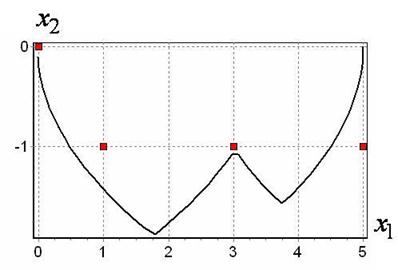
Рис. 2. Траектории на плоскости 
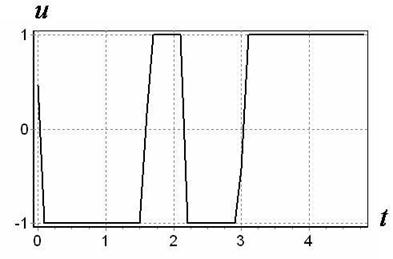
Рис. 3. Управление 
Время движения по всей траектории составило 4.82 с. При оптимальном по быстродействию управлении, при точном прохождении всех точек время движения по траектории составило бы 
с.
Рецензенты:
Дикусар В. В., д.ф.-м.н., профессор, главный научный сотрудник отдела прикладных проблем оптимизации Федерального государственного бюджетного учреждения науки Вычислительного центра им. А. А. Дородницына Российской академии наук, г. Москва.
Забудский Е. И., д.т.н., профессор кафедры электроснабжение и электрические машины Федерального государственного бюджетного образовательного учреждения высшего профессионального образования Московского государственного агроинженерного
университета им. В. П. Горячкина, г. Москва.
Антонов Александр Владимирович, д.т.н., профессор, декан факультета "Кибернетики", Обнинский институт атомной энергетики Национального исследовательского ядерного университета МИФИ Министерства образования и науки РФ, г. Обнинск.