Введение
Однородные цепи с распределенными параметрами имеют постоянные удельные параметры R0 (Ом/км), L0 (Гн/км), G0 (См/км), C0 (Ф/км) [1, 3, 4]. К этим цепям относятся воздушные и кабельные линии связи и электропередачи. В линиях электропередачи при подключении и отключении трехфазного источника питания или трехфазной нагрузки происходят переходные процессы. Возникающие при переходных процессах значительные импульсы напряжений и токов могут вывести из строя электрооборудование линии, источник питания и нагрузку. Переходные процессы связаны с прохождением волнами напряжения и тока линий и с отражениями этих волн от нагрузки и источника. Расчет этих процессов при помощи временных функций с учетом многократных отражений волн сопряжен со значительными трудностями. Поэтому разработка методики применения частотных функций [1, 3] для расчета переходных процессов в однородных цепях с распределенными параметрами, в частности, в линиях электропередачи представляется актуальной задачей, особенно при современном развитии вычислительной техники и стандартных систем компьютерной математики, например, Mathcad [2].
Описание метода
Для использования частотного метода расчета переходных процессов необходимо иметь линейную цепь, к которой применим метод наложения [3], т. е. параметры пассивных элементов цепи R, L, C должны быть постоянны, и обязательны абсолютно интегрируемые функции fИ(t) источников ЭДС и токов, когда ![]() при времени t>0 [1, 3]. В результате спектральные (частотные) функции источников ЭДС и токов определяются при помощи одностороннего прямого преобразования Фурье [1, 3]
при времени t>0 [1, 3]. В результате спектральные (частотные) функции источников ЭДС и токов определяются при помощи одностороннего прямого преобразования Фурье [1, 3]
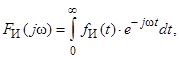
а спектральные функции ![]() напряжений и токов в разных точках линии в функции координаты x и угловой частоты ω находятся с использованием основных комплексных уравнений линий с гиперболическими функциями [1, 3]. Далее функции f(x,t) напряжений и токов переходного процесса рассчитываются с использованием формулы, полученной из обратного преобразования Фурье [3]:
напряжений и токов в разных точках линии в функции координаты x и угловой частоты ω находятся с использованием основных комплексных уравнений линий с гиперболическими функциями [1, 3]. Далее функции f(x,t) напряжений и токов переходного процесса рассчитываются с использованием формулы, полученной из обратного преобразования Фурье [3]:
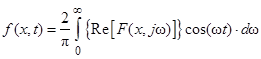 .
.
Синусоидальные функции fИ(t) источников ЭДС и токов не являются абсолютно интегрируемыми, поэтому эти функции будем рассматривать как прямоугольные импульсы с синусным заполнением:
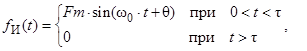
где w0=2pf=314 1/с – угловая частота в линиях электропередачи; t=n×t0 – длительность импульса; ![]() – время пробега волнами напряжения и тока линии длиной l;
– время пробега волнами напряжения и тока линии длиной l;
V0 – (фазовая) скорость перемещения волн в линии при угловой частоте w0;
![]() – задаваемое число пробегов волнами линии l.
– задаваемое число пробегов волнами линии l.
Поскольку преобразование Фурье (1) предполагает fИ(t)=0 при времени t<0, то необходимо применить приведение цепи к нулевым начальным условиям [3]. В этом случае напряжения и токи переходного процесса находятся в виде суммы синусоидальных функций времени, найденных из расчета установившегося режима цепи до коммутации, и функций времени, найденных частотным методом из расчета цепи после коммутации при нулевых начальных условиях.
Будем полагать, что однородная цепь с распределенными параметрами как линия электропередачи работает в симметричном установившемся и переходном режимах [3], когда токи в нулевом проводе и заземлениях нейтралей трехфазного источника и трехфазной нагрузки равны нулю. Поэтому достаточно без учета сопротивлений нулевого провода и заземлений нейтралей рассмотреть одну фазу источника напряжения, линии и нагрузки при постоянных параметрах пассивных элементов, которые могут быть соединены согласно рис. 1, где фазная ЭДС источника равна
![]()
Предположим, что до коммутации в источнике, линии и нагрузке был установившийся режим.
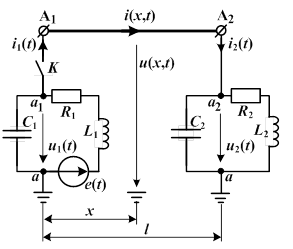
Рис. 1. Расчетная схема на одну фазу (А): R1, L1, C1 и R2, L2, C2 – параметры пассивных элементов источника и нагрузки; u1(t), u(x,t), u2(t) – фазные напряжения; i1(t), i(x,t), i2(t) – линейные токи; l и x – длина линии и расстояние от начала линии
В формулах (1–2) угловая частота w изменяется от 0 до ¥, а время t – от 0 до t. Поэтому для численных расчетов, исходя из быстродействия компьютера и повышения точности расчетов, примем:
Ø по возможности наибольшее число расчетных интервалов, например, N=100; максимальный, например, 100N индекс изменения угловой частоты k =1,2…100N, где k¹0 для предотвращения деления на 0;
Ø шаг интегрирования по времени ht=t0/N; по угловой частоте hw=2p/(tN);
Ø индекс изменения времени q=0,1…nN;
Ø расчетное время tq=q×ht; расчетная угловая частота wk=k×hw.
K – коммутатор (ключ)
В результате согласно (1, 3, 4) спектральная функция источника будет равна:
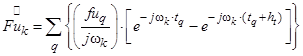 ,
,
где ![]() – числовые значения функции fu(t) в моменты времени tq.
– числовые значения функции fu(t) в моменты времени tq.
Однородная линия характеризуется комплексными, зависящими от расчетной угловой частоты wk, вторичными параметрами [1, 3]:
Ø волновое сопротивление
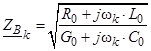 ;
;
Ø постоянная распространения
![]() ;
;
Ø фазовая скорость
![]() ,
,
причем при угловой частоте w0 и постоянной (7) g0=a0+jb0 фазовая скорость равна
![]() .
.
Для указанной на рис. 1 схемы соединения пассивных элементов источника и нагрузки можно записать эквивалентные комплексные сопротивления фазы источника
![]() ;
;
и нагрузки
![]() .
.
В результате, на основании комплексных уравнений линий с гиперболическими функциями [1, 3] определяем входное комплексное сопротивление линии (рис. 1)
относительно зажима А1 с учетом сопротивлений (6) и (9)
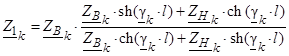 .
.
Рассмотрим расчет переходного процесса в схеме (рис. 1) с использованием приведения этой схемы к нулевым начальным условиям.
Коммутатор K замыкается, в источнике – ненулевые начальные условия, в линии и нагрузке – нулевые начальные условия.
На разомкнутом ключе K из расчета символическим методом [3] цепи источника с ЭДС (4) находим комплексную амплитуду напряжения
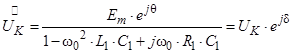 ,
,
числовые значения этого напряжения в моменты времени t=tq
![]() .
.
С учетом (5) и (11) записываем спектральную функцию
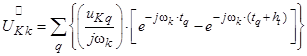 .
.
Далее после замыкания ключа K с использованием формул (6–10, 12) определяем при x=0 спектральную функцию входного тока
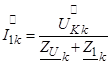
и входного напряжения линии
![]() .
.
На расстоянии х от начала линии на основании уравнений однородной линии в гиперболических функциях [3] и формул (6, 7, 13, 14) можно записать спектральные функции напряжения и тока для угловых частот wk:
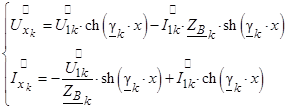 .
.
Согласно (2) с использованием (15) определяем числовые значения напряжения и тока на расстоянии х от начала линии в моменты времени t=tq:
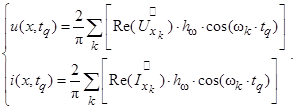
Если зафиксировать координату х от 0 до l, то по вышеприведенным формулам можно численно рассчитать изменение во времени t напряжения и тока в линии.
Результаты
Разработан алгоритм вычислений с использованием системы Mathcad и проведены расчеты напряжений и токов переходного процесса в воздушной линии электропередачи при следующих параметрах [4, 5]: Em=200 кВ; ω0=314 1/с; q=p/2; t=5 мс; t0=1 мс; n=5; R0=0,12 Ом/км; L0=1,36×10–3 Гн/км; G0=9,71×10–9 См/км; C0=8,597×10–9 Ф/км; V0=2,897×105 км/с; R2=10·R1=100 Ом; L2=10·L1=2 Гн; C1=10·C2=5 мкФ.
На рис. 2, 3 (l=289,7 км) и рис. 4, 5 (l=1448,5 км) приведены примеры расчетных зависимостей при замыкании ключа K.
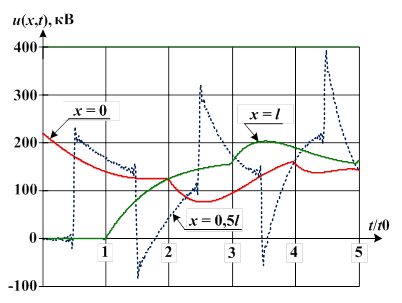
Рис. 2. Расчетные зависимости для напряжений в линии при длине линии l=289,7 км
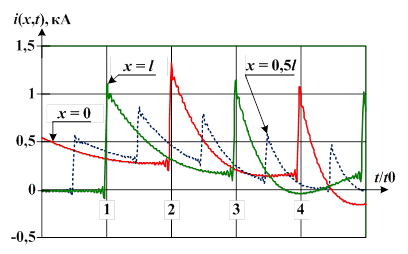
Рис. 3. Расчетные зависимости для токов в линии при длине линии l=289,7 км
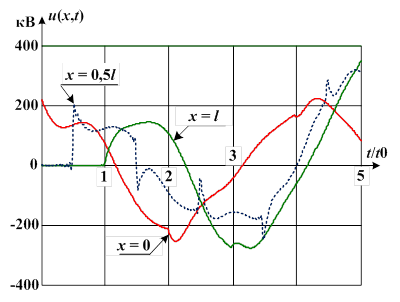
Рис. 4. Расчетные зависимости для напряжений в линии при длине линии l=1448,5 км
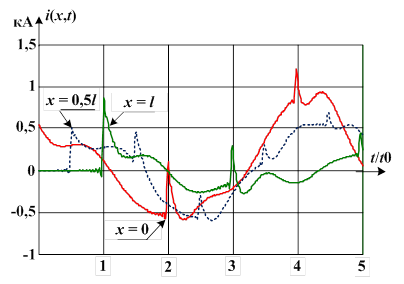
Рис. 5. Расчетные зависимости для токов в линии при длине линии l=1448,5 км
В конце линии при x=l получили напряжение u(l,t0)=0 (рис. 2) и ток i(l,t0)»2×i(0,0) (рис. 3), что соответствует первому моменту прихода падающих волн напряжения и тока в нагрузку, когда емкость С2 является «закороткой».
Частотный метод расчета переходных процессов можно также использовать для линий связи c импульсной ЭДС e(t) произвольной формы.
Выводы
1. Рассмотрено применение частотного метода для расчета переходных процессов в одной фазе нагруженной линии электропередачи при подключении источника напряжения. Показано, что частотный метод достаточно эффективен при использовании стандартных систем компьютерной математики, например, Mathcad.
2. Переходные процессы в линиях рассчитываются с учетом двух переменных: расстояния, отсчитываемого от начала линии, и времени.
3. Методика учитывает многократное прохождение волнами напряжения и тока линии, а также отражение этих волн от нагрузки и источника.
4. Результаты расчетов согласуются с теорией переходных процессов в однородных линиях при различных нагрузках.
5. Использование алгебраических уравнений в комплексной форме вместо дифференциальных уравнений существенно упрощает алгоритм вычислений.
Рецензенты:
Усов Юрий Петрович, д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск.
Федор Юрьевич Канев, д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В. Е. Зуева СО РАН, г. Томск.



