Помехозащищённые быстродействующие алгоритмы экстремального регулирования занимают важное место в теории поисковых систем автоматической оптимизации. Эти системы используются для управления инерционными объектами (энергетическими и химическими установками, ракетными двигателями и т.п.), существенно повышая их технико-экономические показатели [1]. Примером такой системы является система управления процессом электроэрозионной обработки.
Экспериментально установлено, что при электроэрозионной обработке максимальная производительность процесса достигается, когда электрическая мощность, выделяемая в межэлектродном зазоре (МЭЗ), максимальна. Зависимость объёмной интенсивности съёма связки от средней мощности, выделяемой в межэлектродном промежутке, представлена на рисунке 1.
На основании проведенных исследований можно сделать вывод, что для достижения максимальной производительности необходимо процесс электроэрозионного профилирования проводить при максимальной мощности, выделяемой в МЭЗ.
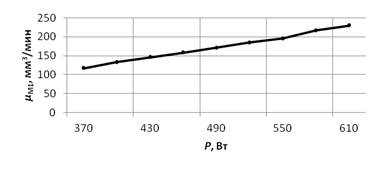
Рисунок 1. Зависимость объёмной интенсивности съёма связки от средней мощности, выделяемой в межэлектродном промежутке
На основе проведенных исследований можно сделать вывод, что для достижения максимальной производительности необходимо процесс электроэрозионного профилирования проводить при максимальной мощности, выделяемой в МЭЗ.
Для этого была разработана функциональная схема автоматического управления приводом подачи электрода-инструмента с экстремальным регулятором мощности. Она включает в себя экстремальный регулятор мощности (ЭРМ), управляющий приводом подачи (ПП) электрода-инструмента (ЭИ). Выход привода подачи подключен к механизму подачи электрода – инструмента, взаимодействующий с обрабатываемой деталью. К электродам электроэрозионного станка подключен генератор технологических импульсов (ГТИ). Мощность, выделяемая в межэлектродном промежутке, измеряется датчиком мощности (ДМ), выход которого соединён с входом экстремального регулятора.
Основная проблема при реализации экстремальных систем управления заключается в обеспечении противоречивых требований точности и устойчивости процедуры поиска экстремума целевой функции. В наибольшей степени этим требованиям удовлетворяют поисковые или шаговые алгоритмы [3].
Недостатком идентификационного алгоритма является сложность идентификации неизвестных параметров целевой функции, что может приводить к значительным ошибкам при вычислении оптимального значения управляющего воздействия и «рысканью» системы экстремального регулирования. Основная проблема при реализации шаговых алгоритмов в реальном времени заключается в обеспечении устойчивости процедуры поиска экстремума, сводящейся к решению, как правило, плохо обусловленной системы линейных алгебраических уравнений [5].
Предлагается совместить достоинства идентификационных и шаговых алгоритмов на основе использования рекуррентного метода наименьших квадратов (РМНК). Во-первых, этот метод применим при достаточно высоких отношениях интенсивностей шума и полезного сигнала, т.е. обладает высокой помехозащищённостью, во-вторых, он даёт надежную сходимость оценок при относительно небольшом объеме вычислений [2], что обеспечивает устойчивость и высокое быстродействие алгоритма экстремального регулирования, построенного на его основе.
Для исследования экстремальной системы привода подачи электрода – инструмента была разработана математическая модель объекта управления. Рассматриваемая система состоит из объекта управления и экстремального регулятора (ЭР) (рисунок 4). Объект управления представляет собой последовательное соединение нелинейного звена с экстремальной характеристикой и линейного инерционного звена с передаточной функцией W(p). На рисунке 2:x – входной сигнал (управляющее воздействие), y – выходной сигнал (целевая функция, экстремум которой следует найти), u – выходной сигнал нелинейного элемента, e – случайная помеха, которая является центрированным случайным процессом типа белого шума.
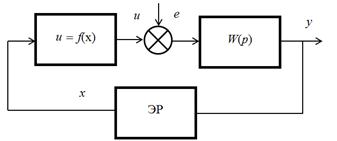
Рисунок 2. Объект управления
Будем считать, что нелинейное звено имеет экстремальную характеристику u=f(x). Инерционное звено может быть описано разностным уравнением n-го порядка:
(1)
где k = 0, 1, 2,…, N – шаг дискретизации, y(k) – выход модели (временного ряда) на k-м шаге; ai – коэффициенты авторегрессии, гдеi=1,…, n; n – количество параметров авторегрессии; bj– коэффициенты скользящего среднего, где j= 1,…, m; m – количество коэффициентов скользящего среднего, u(k) – входной сигнал, e(k) – помеха.
Требуется на каждом шаге вычислительной процедуры поддерживать экстремальное значение целевой функции y(k), реализуя следующий алгоритм экстремального регулирования:
1. Считать входной u(k) и выходной y(k) сигналы экстремального объекта;
2. Вычислить коэффициенты авторегрессии ai и скользящего среднего bj по РМНК;
3. По найденным коэффициентам ai и bj вычислить коэффициент передачи объекта;
4. Осуществить поиск управляющего воздействия u(k), обеспечивающего нулевое значение коэффициента передачи с использованием прямых методов поиска нуля функций.
Очевидно, что при переходе через экстремум коэффициент передачи объекта будет изменять свой знак. Следовательно, задача поиска экстремального значения регулируемого параметра сводится к задаче вычисления текущего значения коэффициента передачи объекта, с последующим нахождением такого управляющего воздействия, при котором коэффициент передачи будет равен нулю.
Значение коэффициента передачи предлагается определить, используя рекуррентный метод наименьших квадратов (РМНК), отличающийся гарантированной сходимостью оценок и требующий сравнительно небольшого объема вычислений.
Алгоритм РМНК может быть представлен в следующем виде 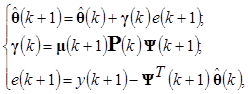[2]:
(2)
где 
– вектор параметров модели; 
– вектор данных; 
– вектор коррекции; 
– весовая матрица; 
– весовая матрица, рассчитанная на следующем шаге;
– начальные значения переменных, причем α – достаточно большое число, I – единичная матрица соответствующей размерности.
Коэффициент передачи объекта k0 вычисляется на основании теоремы о конечном значении дискретной передаточной функции:
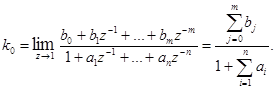(3)
Поиск нуля k0 может осуществляться одним из известных методов [5], например, дихотомии, золотого сечения, Ньютона.
Тогда при поддержании экстремального значения целевой функции y(k) на каждом шаге вычислительной процедуры реализуется следующий алгоритм экстремального регулирования:
1. Считать входной u(k) и выходной y(k) сигналы экстремального объекта;
2. Вычислить коэффициенты авторегрессии ai и скользящего среднего bj по РМНК;
3. По найденным коэффициентам ai и bj , вычислить коэффициент передачи объекта;
4. Осуществить поиск управляющего воздействия u(k), обеспечивающего нулевое значение коэффициента передачи с использованием прямых методов поиска нуля функций.
Для проверки предложенного алгоритма вычисления k0 была разработана Simulink-модель объекта с экстремальной характеристикой. Структурная схема модели соответствует структурной схеме системы, изображённой на рисунке 2. Модель состоит из экстремального объекта, включающего в себя звено с экстремальной характеристикой и три последовательно соединенных апериодических звена. График экстремальной характеристики (кривая 1) представлен на рисунке 3.
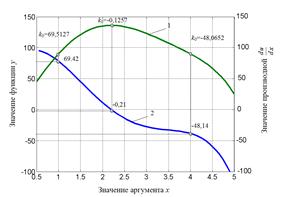
Рисунок 3. График экстремальной характеристики
В первом приближении коэффициент передачи нелинейного звена будет равен производной от его статической характеристики (кривая 2) на рисунке 3. При изменении входного сигнала нелинейного звена x изменяется и его коэффициент передачи, как это видно на рисунке 3.
На рисунке 4 а, б, в показаны осциллограммы входного, выходного сигналов объекта и его коэффициенты передачи, вычисленные по формулам (2) и (3) для постоянных значений входного сигнала нелинейного элемента x0. Помеха имитировалась подачей на вход случайного сигнала, уровень которого соизмерим с уровнем входного сигнала x0.
а)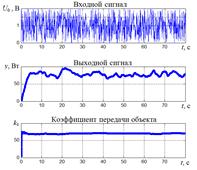
б)
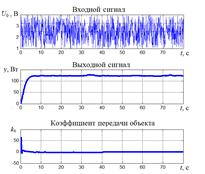в)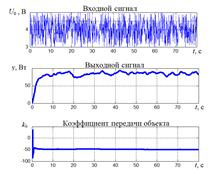
Рисунок 4. Осциллограммы входного, выходного сигналов объекта и его коэффициенты передачи
Сравнение вычисленных коэффициентов передачи экстремального объекта с их значениями, полученными в результате дифференцирования статической характеристики, показывает приемлемую точность определения коэффициента передачи по предлагаемому алгоритму. Относительная приведённая погрешность в определении коэффициента передачи объекта не превышает 5 %.
Для проверки предложенного алгоритма разработанная в Simulink модель системы дополнялась M-функцией, реализующей разработанный алгоритм. Поиск нуля k0 осуществлялся методом Ньютона.
Дрейф экстремальной характеристики моделировали путем подачи на вход системы гармонического низкочастотного воздействия, к которому добавляются высокочастотные помехи.
Результаты моделирования показаны на рисунке 5. Осциллограммы входного сигнала показаны на рисунке 5 а), управляющего воздействия – на рисунке 5 б), сигнал на входе нелинейного элемента – на рисунке 5 в), сигнал на выходе нелинейного элемента – на рисунке 5 г).
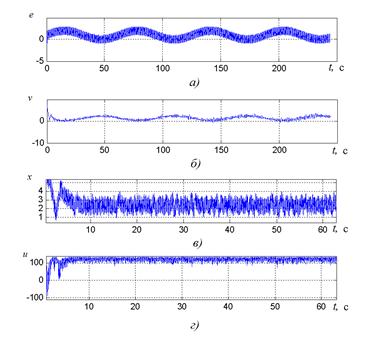
Рисунок 5. Результаты моделирования
Анализ осциллограмм, приведённых на рисунке 5, позволяет сделать вывод, что даже при действии сильных помех, уровень которых соизмерим с уровнем входного сигнала, система экстремального регулирования удерживает координаты объекта в области экстремальных значений его целевой функции.
Фазовая траектория располагается в окрестности точки, в которой целевая функция достигает экстремума (максимума). Несмотря на высокий уровень помех, отклонение системы от точки экстремума не превышает 24 %, что подтверждает эффективность предлагаемого алгоритма.
Заключение
Разработан алгоритм поиска экстремума характеристики инерционного объекта по текущим измерениям его входа и выхода с использованием рекуррентной процедуры метода наименьших квадратов, в результате которой оценивается коэффициент передачи объекта, а затем с использованием прямых методов поиска нуля функции находится его нулевое значение.
В результате моделирования работы алгоритма установлено, что он обеспечивает сходящиеся значения оценки коэффициента передачи, устойчиво удерживая объект в окрестности точки экстремума, даже при наличии сильных возмущений.
Относительная приведённая погрешность в определении коэффициента передачи объекта не превышает 5 %, отклонение системы от точки экстремума не более 24 %, при отношении сигнал / шум, близком к единице. Время поиска экстремума соизмеримо со временем переходного процесса объекта регулирования.
Данная работа выполнена в рамках конкурса «Поддержка развития внутрироссийской мобильности научных и научно-педагогических кадров путем выполнения научных исследований молодыми учеными и преподавателями в научно-образовательных центрах» по ГК № 14. В 37.21.0160.
Рецензенты:
Дзлиев Сослан Владимирович, д.т.н., профессор кафедры ЭТПТ Санкт-Петербургского государственного электротехнического университета, руководитель лаборатории «МОЛ СЭТ», г. Санкт-Петербург.
Демидович Виктор Болеславович, д.т.н., профессор кафедры ЭТПТ Санкт-Петербургского государственного электротехнического университета, г. Санкт-Петербург.