Введение
Создание МР (мобильных роботов), обладающих развитыми возможностями самостоятельного формирования маршрута и продвижения по нему, а также автоматического решения поставленных перед ним задач, является на текущий момент актуальной задачей. Учитывая это, особенно большое значение приобретают интеллектуальные системы управления, позволяющие осуществлять автономное функционирование МР и решение целевых задач в априори неизвестных условиях и наличии некоторой степени неопределенности данных.
На текущий момент существуют три основных типа построения интеллектуальных систем управления и навигации МР:
· Архитектура, основывающаяся на применении функциоaнальной декомпозиции по принципу: «распознавание – моделирование – планирование – осуществление».
· Реактивная (рефлексная) – данная архитектура использует стратегию целенаправленного поведения робота, что достигается за счет применения нейросетевых систем управления или систем, построенных на базе нечеткой логики.
· Гибридная система, чья архитектура интегрирует в себе две предыдущие.
В данной статье предлагается использование функциональной декомпозиции для построения системы навигации и управления. Для этого осуществляется дифференциация общей задачи на группу подзадач. Решение каждой подзадачи формирует исходные данные для решения следующей в группе. В качестве подзадач выступают: задача стратегического планирования, тактического планирования и задача исполнения. Для решения каждой из подзадач моделируется отдельный модуль. Опираясь на данные, полученные от СТЗ (системы технического зрения), память МР, датчики и другие источники информации каждый из них формирует управляющее воздействие, передающееся по иерархической цепочке.
1. Анализ задачи навигации и управления мобильного робота
Задачу навигации и управления можно разделить на три уровня:
· Стратегический уровень планирования. На данном уровне решается вопрос глобальной навигации.
· Тактический уровень планирования. Задача тактического уровня сводится к решению задачи локальной навигации.
· Исполнительный уровень. Задачей данного уровня является обеспечение заданных характеристик движения МР в каждый момент времени посредством приводов.
Таким образом, для решения поставленной задачи необходимо решить три подзадачи: построение глобальной навигации, построение локальной навигации, построение системы управления исполнительными движениями МР.
2. Решение задачи глобальной навигации
Задача глобальной навигации сводится к отысканию такого маршрута из вершины текущей локации к вершине необходимой локации, для которого суммарная стоимость всех его переходов имела бы минимальное значение. Для разрешения данной задачи существует несколько алгоритмов гарантированного нахождения оптимального пути (в случае связного графа. Но все алгоритмы обладают существенным недостатком – высокие вычислительные затраты.
В связи с этим предлагается применение генетических алгоритмов (ГА) отыскания оптимального пути. Данный тип алгоритмов не гарантирует нахождения оптимального пути, но обеспечивает монотонное снижение стоимости маршрута по мере его функционирования. Иначе говоря, каждая новая итерация алгоритма находит такой же или более оптимальный маршрут. При достижении приемлемой «стоимости» маршрута, выполнение алгоритма можно прекратить.
3. Решение задачи локальной навигации
Решение задачи локальной навигации МР реализуется при помощи метода потенциалов. Основные идеи этого метода были предложены А. К. Платоновым в работе (7). Обзор и различные модификации данного метода можно найти в работах (8), (9), (10).
Суть предлагаемого метода заключается в следующем: целевая точка выступает в роли виртуального положительного заряда. Препятствия, так же как и МР, несут виртуальный отрицательный заряд. Под действием сил притяжения МР притягивается к целевой точке и отталкивается от препятствий.
В качестве целевой точки выступает центр очередной локации, определенный при помощи алгоритма глобальной навигации.
Препятствия аппроксимируются выпуклыми фигурами. В частности, в данной работе предлагается использование эллипсов.
Таким образом, для решения задачи локальной навигации необходимо располагать следующими сведениями:
· координаты целевой точки;
· координаты текущего местоположения;
· координаты фокусов (
) каждого из эллипсов и их эксцентриситеты (
).
Для построения данного алгоритма необходимо определить правило, определяющее формирование силового поля целевой точкой и препятствиями, а также принцип, определяющий воздействие данного поля на МР.
4. Решение задачи управления исполнительными движениями мобильного робота
Задача управления МР может быть разбита на две подзадачи:
· Выработка значений угловых частот колес МР, обеспечивающих движение по физически реализуемой траектории с вектором скорости, заданным системой локального управления.
· Обеспечение полученных значений угловых частот МР при помощи системы приводов.
Первая подзадача относится к кинематическим задачам, и для её разрешения необходимо построение кинематической модели МР.
Вторая подзадача относится к задачам динамики и учитывает инерционные свойства МР, приводов и.т.п. Для её разрешения требуется построение динамической модели МР и, в частности, системы приводов.
Каждая из подзадач решается соответствующей подсистемой: кинематическая решается кинематической подсистемой, динамическая – динамической подсистемой.
4.1. Кинематическая модель мобильного робота
При построении кинематической модели будем полагать, что влиянием третьего колеса (ведомого) можно пренебречь. Кроме того, при движении отсутствует проскальзывание, т.е. имеем случай идеального сцепления колесной пары с поверхностью дороги. Рассмотрим положение робота в некоторый момент времени. Расположим вспомогательную, неподвижную систему координат 
так, чтобы её центр совпадал с центром масс МР, а направление оси 
определяло направление поступательного движения робота. Угол 
определяет поворот системы координат , а следовательно, и МР относительно 
.
Положительным направлением вращения будем считать вращение против часовой стрелки. Тогда, в системе координат , формулы кинематической связи угловых скоростей вращения правого (
) и левого (
) колеса со скоростями изменения положения МР в пространстве можно представить в следующем виде:
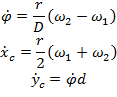
Или в матричном виде:
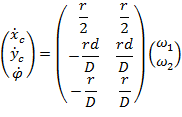(4.1)
Для пересчета в основную () систему координат, очевидно, применимы формулы:
Тогда с учетом 4.1 получаем следующую зависимость для скоростей:
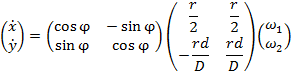
Или в более компактной форме:
(4.2)
где:
.
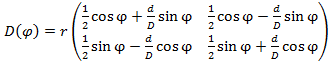Причем, 
есть функция времени и определяется как:
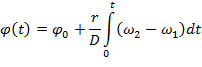(4.3)
где: 
– положение МР в начальный момент.
4.2. Построение кинематического регулятора
Задача кинематического регулятора – выработка управляющего сигнала для объекта управления, в качестве которого выступает динамическая подсистема МР, такого, чтобы реальный вектор скорости стремился к желаемому. При этом осуществляемая траектория движения должна быть физически реализуемой. Для решения этой проблемы наложим дополнительное ограничение на кинематический регулятор: в процессе управления направление вектора скорости должно стремиться к направлению вектора, определяющего ориентацию МР (ось ).
Несложно видеть, что выполнение этого ограничения требует, чтобы 
стремилось к нулю, т.е. выполнялось:
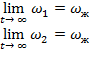(4.4)
где: 
– желаемая частота вращения колес МР.
Рассмотрим подсистему объекта управления, определяющую его ориентацию в пространстве. Она представлена формулой 4.3. Из этого уравнения несложно видеть, что для позиционирования робота по заданному вектору 
при условии, что 
необходимо, чтобы имело место:
С другой стороны, по окончании регулирования должно выполняться соотношение 4.4.
Кроме того, исходя из вышесказанного, одним из показателей степени завершенности процесса регулирования является сигнал рассогласования между текущей и желаемой ориентацией МР 
.
Тогда несложно видеть, что общим видом закона регулирования будет:
(4.5)
Ограничимся рассмотрением нединамического регулятора. То есть потребуем, чтобы функции 
не зависели явным образом от производных. Кроме того, учитывая симметричность МР, резонно потребовать от функций их подобия, т.е.:
Легко проверить, что наложенным на функции требованиям удовлетворяет регулятор:
(4.6)
Чем больше величина 
, тем меньше потребуется времени для достижения МР желаемого вектора скорости (с установленным диапазоном допустимой погрешности). Однако выбор ограничивается возможностями динамической подсистемы.
4.3. Динамическая модель мобильного робота
В качестве приводов в данной работе используются двигатели постоянного тока с якорным управлением, осуществляющие раздельное вращение правого и левого колес. Пренебрежем внутренним сопротивлением источника питаний, генерирующего напряжение 
. Тогда для получения динамической модели МР необходимо определить момент нагрузки 
.
Составим систему уравнений:
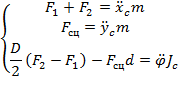
где: 
– момент инерции МР относительно центра масс;
– масса МР;
– сила сцепления колес с поверхностью дороги.
– силы действующие соответственно на правое и левое колеса.
Из кинематической модели МР (формула 4.1) следует:
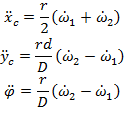
Тогда получаем систему уравнений:
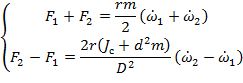
Отсюда имеем формулы для моментов:
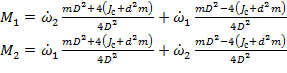(4.8)
Очевидно, что в виду симметрии МР регуляторы 1 и 2 должны быть одинаковыми. В качестве них выберем ПИД регулятор.
Настройка параметров ПИД регулятора, таких как
, 
и может быть осуществлена посредством использования таких алгоритмов, как имитация отжига, метод градиентного спуска, ГА и.т.д.
Заключение
· Предложено решение глобальной навигации посредством ГА.
· Решение задачи локальной навигации с помощью метода виртуального силового поля.
· Была решена задача управления МР. Для этого МР был представлен в виде двух подсистем: кинематической и динамической. Были получены кинематическая и динамическая математические модели МР в виде структурных схем. Также были выбраны и представлены в виде математических моделей кинематический и динамический регуляторы, позволяющие осуществлять движение с параметрами, заданными системой локальной навигации.
Рецензенты:
Поляхов Николай Дмитриевич, д.т.н., профессор кафедры САУ Санкт-Петербургского государственного электротехнического университета, г. Санкт-Петербург.
Прокофьев Геннадий Иванович, д.т.н., профессор, заведующий кафедрой РАПС Санкт-Петербургского государственного электротехнического университета, г. Санкт-Петербург.