1. О С-точной паре натуральных переменных и сюръективности инъективных отображений φ: N→N
Под переменной ниже понимается, по умолчанию, тройка (x, А, θ), где x - символ переменной, А - множество значений переменной и θ - порядок во множестве А и если А ⊆ N, тогда θ означает, по умолчанию, естественный порядок множества A, как подмножества множества натуральных чисел. Бесконечность множества N понимается в связи с принципом математической индукции как неограниченная возможность перехода от (n) к (n+1), а фраза «при предельном переходе в F(n)» означает следующее:
![]()
![]() . (1.1)
. (1.1)
Принцип предельного перехода (1.1) и равномерная направленность множества N мотивируют, почти точно следуя одинаково упорядоченным переменным Г. М. Фихтенгольца [6, с. 643-644], введение понятия С-точной пары, которое излагается здесь в более общей формулировке, чем в [5, с. 84].
Пусть множества А ⊂N и В ⊂N бесконечны, и ![]() и Е
и Е ![]() A ∪ B ⊆ N.
A ∪ B ⊆ N.
Определение 1.1. Пара (m, k) натуральных переменных m∈A и k∈B называется С-точной парой, если для каждых соседних в Е элементов m и k найдётся число С>0 такое, что
|m-k|<C. (1.2)
Условие (1.2) C-точности пары (n, m) имеет следующую эквивалентную, что очевидно, форму записи:
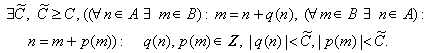 (1.2')
(1.2')
Ниже, по умолчанию, рассматриваются инъективные функции φ: N→N. Последовательность натуральных чисел ξ ![]() {1,n1, n2, ....,ni...} ⊂ N, называется последовательностью с ограниченным шагом, если ∃
{1,n1, n2, ....,ni...} ⊂ N, называется последовательностью с ограниченным шагом, если ∃![]() ∈N такое, что при N(ξ)
∈N такое, что при N(ξ) ![]() (i: ∃ni ∈ξ } ⊂ N ∀i ∈ N (ξ) 0<ni - n < ,
(i: ∃ni ∈ξ } ⊂ N ∀i ∈ N (ξ) 0<ni - n < , ![]() . Пусть далее,
. Пусть далее, ![]()
![]()
![]() . Последовательность ξ и инъективное отображение φ: N→N определяют две последовательности {
. Последовательность ξ и инъективное отображение φ: N→N определяют две последовательности {![]() } и {
} и {![]() },
}, ![]() , неотрицательных целых чисел следующим образом:
, неотрицательных целых чисел следующим образом:
![]()
![]()
![]() {φ(n)-
{φ(n)- ![]() }≥0,
}≥0, ![]()
![]() |
| ![]() |≥0,
|≥0, ![]()
![]()
![]() \φ(
\φ(![]() ). (1.3)
). (1.3)
Если ![]()
![]() φ(
φ(![]() )\
)\ ![]() и
и ![]()
![]() |
| ![]() |≥0, то очевидно, что 0≤
|≥0, то очевидно, что 0≤ ![]() =
=![]() ≤
≤![]() . Действительно,
. Действительно,![]() =
=![]() , если {p , ni < p<δi, ∀n ≤ni p≠ φ (n)}= Ø. В иных случаях
, если {p , ni < p<δi, ∀n ≤ni p≠ φ (n)}= Ø. В иных случаях ![]() . Отображение φ: N→N определяет также последовательность {
. Отображение φ: N→N определяет также последовательность { ![]() }
}![]() целых чисел формулой
целых чисел формулой ![]() . Если
. Если ![]() и для некоторой последовательности ξ
и для некоторой последовательности ξ ![]() , то очевидно, что
, то очевидно, что ![]() . Легко доказать следующее
. Легко доказать следующее
Утверждение 1.1. Для всякого инъективного отображения φ: N → N существует последовательность ξ такая, что
![]() =
= ![]() . (1.4)
. (1.4)
Непосредственное и очевидное следствие определения множества ![]() в (1.3) и определения сюръективности отображения φ имеет [5, c. 88] вид:
в (1.3) и определения сюръективности отображения φ имеет [5, c. 88] вид:
Утверждение 1.2. Необходимое условие сюръективности каждого инъективного отображения φ: N → N имеет следующие две эквивалентные формы:
![]() Ø и
Ø и ![]() . (1.5)
. (1.5)
Ниже для краткости изложения фраза «для почти всех i» обозначает «за исключения конечного множества индексов i» и по определению мы пишем « ![]() ».
».
Достаточные признаки сюръективности (а) и антисюръективности (b) функции φ: N → N изложены в терминах последовательности {![]() } ниже.
} ниже.
Утверждение 1.3. Достаточные условия антисюръективности (а) и сюръективности (b) инъективного отображения φ: N → N имеют, соответственно, вид
(a) ![]() , (1.6)
, (1.6)
(b) ![]() . (1.7)
. (1.7)
● Каждое число ![]() определяет количество элементов n из подмножества
определяет количество элементов n из подмножества ![]() , не имеющих прообраза
, не имеющих прообраза ![]() в ,
в ,![]() поэтому неограниченность последовательности {
поэтому неограниченность последовательности { ![]() },
}, ![]() , противоречит условию
, противоречит условию ![]() сюръективности отображения φ. Условие (1.7) гарантирует существование числа
сюръективности отображения φ. Условие (1.7) гарантирует существование числа ![]() такого, что
такого, что ![]() для отображения φ справедлива следующая цепь импликаций:
для отображения φ справедлива следующая цепь импликаций:
![]() . ■
. ■
Про антисюръективное инъективное отображение скажем, что оно потенциально не осуществимо на всем множестве N.
Как показывают примеры, условия (1.6) и (1.7) не являются необходимыми для антисюръективности и сюръективности, соответственно, отображения φ.
В [5, c. 86] доказано следующее ниже
Утверждение 1.4 Последовательности ![]() и
и ![]() ,
,![]() , определяемые парой (ξ, φ), удовлетворяют одному и только одному из трёх следующих условий:
, определяемые парой (ξ, φ), удовлетворяют одному и только одному из трёх следующих условий:
(a) ![]()
![]()
![]() , (1.8)
, (1.8)
(b) (∃ C1, C2, c2 ≤ C1 ∈N) : ![]()
![]() , (1.9)
, (1.9)
(c) i ∈N(ξ) ![]()
![]() . (1.10)
. (1.10)
Следствие Утверждений 1.1-1.4 записано ниже [3, p. 8; 4]:
Теорема 1.1. Ограниченность последовательности {φn } целых чисел ![]() ,
, ![]() , является необходимым условием сюръективности инъективного отображения φ: N → N , то есть из φ(N) = N следует, что
, является необходимым условием сюръективности инъективного отображения φ: N → N , то есть из φ(N) = N следует, что
![]() (φ (n) : n) = 1. (1.11)
(φ (n) : n) = 1. (1.11)
Как показывают примеры, необходимые условия (1.5) и (1.11) сюръективности инъекции φ: N → N являются независимыми и, следовательно, ни одно из этих условий не может быть достаточным.
Утверждение 1.5. Инъективное отображение φ* : N → N , определяющее некоторую последовательность ![]() где
где ![]() , с неограниченным шагом является антисюръективным или, другими словами, будет неосуществимо на всём множестве N.
, с неограниченным шагом является антисюръективным или, другими словами, будет неосуществимо на всём множестве N.
● Пусть, ![]() будет последовательностью с неограниченным шагом, т. е. для отображения φ*, определяющего
будет последовательностью с неограниченным шагом, т. е. для отображения φ*, определяющего ![]() ,
,
![]() . (1.12)
. (1.12)
Пусть теперь последовательность ξ ⊂ N такова, что ∀i ∈N(ξ) ni = i+1. Значит, для ∀i ∈N(ξ) ![]() и в этом случае, так как δi
и в этом случае, так как δi ![]()
![]() {φ(n)- ni} (см. (1.3))
{φ(n)- ni} (см. (1.3)) ![]() , i ∈N(ξ). Поэтому ∀i ∈N(ξ)
, i ∈N(ξ). Поэтому ∀i ∈N(ξ)
![]() (mi+1 -(i+2))-( mi - i - 1)= mi+1- mi-1.
(mi+1 -(i+2))-( mi - i - 1)= mi+1- mi-1.
Таким образом, в силу условия (1.12) неравенство ![]() С-1 справедливо для i(С) ∈N(ξ). Следовательно,
С-1 справедливо для i(С) ∈N(ξ). Следовательно, ![]() -1+С. Неограниченность последовательности
-1+С. Неограниченность последовательности ![]() , i ∈N(ξ), определяемой парой (ξ, φ*), следует из последнего неравенства в силу произвольности в (1.12) числа С. Значит, отображение φ* , задающее последовательность ξ* из условия теоремы, является антисюръективным в силу условий (1.7)-(1.10). ■
, i ∈N(ξ), определяемой парой (ξ, φ*), следует из последнего неравенства в силу произвольности в (1.12) числа С. Значит, отображение φ* , задающее последовательность ξ* из условия теоремы, является антисюръективным в силу условий (1.7)-(1.10). ■
Утверждение 1.5 очевидным образом имплицирует следующую теорему.
Теорема 1.2. Пусть A ![]() {n}⊆ N и B
{n}⊆ N и B ![]() {m}⊆ N являются бесконечными подмножества множества N. Тогда существует число C ∈ N такое, что пара (n, m) переменных n и m является C-точной парой переменных (1.2).
{m}⊆ N являются бесконечными подмножества множества N. Тогда существует число C ∈ N такое, что пара (n, m) переменных n и m является C-точной парой переменных (1.2).
Замечание 1.1. Легко показать, что содержание доказанных выше утверждений сохраняется для инъективных отображений φ: А→А, где А ⊂ N.
Классификация инъективных отображений φ: N → N проводится по следующим двум признакам:
1) тривиальность, не тривиальная ограниченность, неограниченность последовательности {δi}, i ∈N(ξ),
2) выполнение или невыполнение условия: ![]()
![]() .
.
Утверждения 1.1 -1.4 позволяют разбить все инъективные отображения φ: N → N на шесть непересекающихся классов следующим образом (ср. [5, c. 87-88]).
Определение 1.2. Инъективное отображением φ: N → N называется точно сюръективным, если существует такая последовательность ξ=(1,n1, n2, ....,ni, ... ), что для ![]() δi =0.
δi =0.
Определение 1.3. Инъективное отображение φ: N → N называется потенциально сюрьективным, если выполняются следующие два условия:
а) для любой последовательности ξ=(1,n1, n2, ....,ni, ... ) существует число ![]() >0 такое, что для
>0 такое, что для ![]() 0< δi ≤
0< δi ≤ ![]() ,
,
b) ![]()
![]() .
.
Определение 1.4. Инъективное отображением φ: N → N называется потенциально антисюръективным, если выполняются следующие два условия:
а) существует такая последовательность ξ=(1,n1, n2, ....,ni, ... ), что для любого числа С>0 найдётся такое число i (ξ , C) ∈N(ξ), что ![]() >С,
>С,
b) ![]()
![]() .
.
Определение 1.5. Инъективное отображение φ: N → N называется С-конечно антисюръективным, если последовательность {δi}, определяемая парой (φ, ξ), является ограниченной последовательностью и, кроме того,
∃(С, i0, Nφ ) С>0, i0 ∈N(ξ), Nφ ⊂ N:∀i > i0 Nφ ⊂ Di и | Nφ | = C. (1.13)
Очевидно, что подмножество Nφ не пересекается с образом φ (N )отображения φ: N → N : ![]() .
.
Определение 1.6. Инъективное отображением φ: N → N называется t-антисюръективным, если соответствующая последовательность {δi} является не ограниченной последовательностью и, кроме того, для этого отображения выполняется условие (1.13)
Определение 1.7. Инъективное отображением φ: N → N называется тотально антисюръективным, если для этого отображения подмножество Nφ множества N, ![]() , является бесконечным множеством.
, является бесконечным множеством.
Инъективные отображения φ: N → N допускают аналогичную классификацию для каждого бесконечного собственного подмножества A ⊂ N.
Заключение 1.1. Для каждого антисюръективного инъективного отображения φ: N → N существует пара (N1, N2 ) таких бесконечных собственных подмножеств N1 и N2 множества N, что ![]() и
и ![]() , где
, где ![]() .
.
Например, множество E ![]() {k: ∃n ∈N , k=2n} есть множество чётных натуральных чисел, E ⊂ N . При этом очевидно, что отображение φ: N → N, заданное формулой φ(n)
{k: ∃n ∈N , k=2n} есть множество чётных натуральных чисел, E ⊂ N . При этом очевидно, что отображение φ: N → N, заданное формулой φ(n)![]() k=2n, является тотально антисюръективным. Тогда, в соответствии с Заключением 1.1, E= N2 и N1={k: k ∈ N, ∃n ∈N, k= n/2} , (см. также п.3).
k=2n, является тотально антисюръективным. Тогда, в соответствии с Заключением 1.1, E= N2 и N1={k: k ∈ N, ∃n ∈N, k= n/2} , (см. также п.3).
2. О сходимости числовых последовательностей
Числовая последовательность (а)![]() {
{ ![]() называется сходящейся к конечному числу А, если lim (an) = A. В противном случае, то есть если lim (an) не существует или равен ± ∞, последовательность (a) называется в анализе расходящейся (DS). Числовая последовательность (a) называется в анализе фундаментальной или последовательностью Коши (CS), если для неё выполняется условие
называется сходящейся к конечному числу А, если lim (an) = A. В противном случае, то есть если lim (an) не существует или равен ± ∞, последовательность (a) называется в анализе расходящейся (DS). Числовая последовательность (a) называется в анализе фундаментальной или последовательностью Коши (CS), если для неё выполняется условие
![]()
![]() . (2.1)
. (2.1)
Условие (2.1) имеет [7, p. 355] эквивалентную, но более конкретную форму:
![]() . (2.2)
. (2.2)
Эта форма определения фундаментальной последовательности показывает, что пару (m, n) в (2.2) можно считать (Теорема 1.2) С-точной парой (1.2).
Очевидно, что {(a)}={CS} ∪ {DS}. В анализе принято также считать, что
{CS} ∩ {DS}=Ø. (2.3)
Для критического анализа равенства (2.3) мы введём следующее новое в теории числовых последовательностей понятие [ср. 5, с. 96].
Определение 2.1. Числовая последовательность (a) называется е-расходящейся (е-DS), если существуют такие две бесконечные подпоследовательности ![]() , что выполняется следующее условие:
, что выполняется следующее условие:
![]() (2.4)
(2.4)
Сравнением условий (2.1)-(2.2) и (2.4) доказывается следующая теорема.
Теорема 2.1. Всякая числовая последовательность является либо фундаментальной последовательностью, либо е-расходящейся, то есть
∀(a) (a) ∈ {CS} ∪ {е-DS} и {CS} ∩ {е-DS}=Ø. (2.5)
Легко показать, что
{e-DS} ⊆ {DS} (2.6)
Пример последовательности { ![]() ,
, ![]() , 0<α<1, показывает, что
, 0<α<1, показывает, что
{e-DS} ⊂ {DS}. (2.7)
• Последовательность ![]() является расходящейся, так как при 0<α<1
является расходящейся, так как при 0<α<1 ![]() . С другой стороны, в силу бесконечности в (2.4) подмножеств-последовательностей
. С другой стороны, в силу бесконечности в (2.4) подмножеств-последовательностей ![]() , пара (m , n) переменных m>
, пара (m , n) переменных m> ![]() , m ∈ξ1 , и n>
, m ∈ξ1 , и n>![]() , n ∈ξ2 , является (Теорема 1.2) С- точной парой (1.2'). Поэтому существует сколь угодно много таких пар
, n ∈ξ2 , является (Теорема 1.2) С- точной парой (1.2'). Поэтому существует сколь угодно много таких пар ![]() ∈ (ξ1 ,ξ2 ) что
∈ (ξ1 ,ξ2 ) что ![]() , где числа q(
, где числа q(![]() ),
), ![]() , являются членами ограниченной последовательности целых чисел. Далее мы рассмотрим функцию
, являются членами ограниченной последовательности целых чисел. Далее мы рассмотрим функцию ![]() , определённую формулой
, определённую формулой ![]() . Очевидно, что значение
. Очевидно, что значение ![]() функции f совпадает с разностью
функции f совпадает с разностью ![]() при
при ![]() . Легко показать, что при
. Легко показать, что при ![]()
![]() . Следовательно, условие (2.5) будет нарушено, по крайней мере, для одной какой-нибудь пары
. Следовательно, условие (2.5) будет нарушено, по крайней мере, для одной какой-нибудь пары ![]() ∈ (ξ1 ,ξ2 ) значений
∈ (ξ1 ,ξ2 ) значений ![]() >
> ![]() и
и ![]() >
> ![]() . Это доказывает, что последовательность {
. Это доказывает, что последовательность { ![]() }, 0e-расходящейся. ■
}, 0e-расходящейся. ■
Поэтому вместо условия (2.6) имеет место строгое включение (2.7). И, следовательно, с учётом (2.5) вместо (2.3) справедливо неравенство
{CS} ∩ {е-DS} ≠ Ø (2.8)
Введём важное для дальнейшего изложения ещё одно понятие [5, с. 97].
Определение 2.2. Числовая последовательность (a) называется w-сходящейся (w-CS), если для неё выполняется следующее условие:
![]()
![]() . (2.9)
. (2.9)
Сейчас мы докажем главное утверждение этой статьи, используя Определение 2.1 е-расходящейся последовательности и понятие С-точной пары (1.2').
Теорема 2.2. Множество фундаментальных последовательностей совпадает с множеством w-сходящихся последовательностей
{CS}={w-CS}. (2.10)
• Предположим противное, что существует числовая последовательность (a), удовлетворяющая условию (2.9), но не являющаяся фундаментальной. Тогда в силу (2.5) она будет е-расходящейся, то есть для неё справедливо условие (2.4). В силу бесконечности последовательностей ξ1 ,ξ2 в (2.4) пара (m, k) переменных, (m, k) ∈ (ξ1 ,ξ2 ) , является С-точной парой (см. (1.2) и (1.2')). Тогда, по крайней мере, для одного q0 ∈ N, 0< q0 < ![]() , существует бесконечное множество таких пар
, существует бесконечное множество таких пар ![]() ,
, ![]() , что
, что ![]() , например, и, в силу (2.4)
, например, и, в силу (2.4)
![]() (2.11)
(2.11)
С другой стороны, пусть в (2.9) ![]() . Тогда в силу неравенства
. Тогда в силу неравенства
![]()
и условия (2.9) имеет место ![]() следующая оценка:
следующая оценка:
![]() (2.12)
(2.12)
Пусть ![]() . Неравенство (2.12) справедливо для всех n, n> n** , в том числе, и при n = k* :
. Неравенство (2.12) справедливо для всех n, n> n** , в том числе, и при n = k* : ![]() Это противоречит (2.11). ■
Это противоречит (2.11). ■
Следствие Теоремы 2.2. Не всякая фундаментальная последовательность (а) ограничена конечным числом.
Например, последовательность ![]() удовлетворяет условию (2.9), но её предельное значение больше любого конечного числа. Каждую такую числовую последовательность мы будем обозначать символом ILCS.
удовлетворяет условию (2.9), но её предельное значение больше любого конечного числа. Каждую такую числовую последовательность мы будем обозначать символом ILCS.
3. О бесконечно больших числах
Следствие Теоремы 2.3 мотивирует введение следующего понятия.
Определение 3.1. Предельное значение фундаментальной последовательность (а), не ограниченной конечным числом, мы называем бесконечно большим числом (ILN), определяемым этой последовательность (а), и пишем 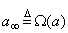 .
.
В нестандартном анализе о ILN говорят (см. [1, с. 16, 21 и далее]) как о нестандартных, неосуществимых, актуально бесконечно больших или недоступных числах. Мы множеству {ILN} припишем символ Ω.
Утверждение 3.1. Последовательность (а), определённая для всех n∈N формулой ![]() , a>0, является фундаментальной.
, a>0, является фундаментальной.
•![]() ■
■
Однако, последовательность (а), определённая для всех n∈N формулой an = a • n , является для всех a ≠ 0 е-расходящейся, что очевидно.
Утверждение 3.1 допускает следующее обобщение - переход от теории последовательностей к анализу функций:
Теорема 3.1. Неограниченная дифференцируемая в ± ∞ функция ![]() сходится к соответствующему ILN Ω (f) тогда и только тогда, когда
сходится к соответствующему ILN Ω (f) тогда и только тогда, когда ![]() .
.
•Предельный переход в формуле Лагранжа, записанной для функции f:
![]() ,
,
составляет доказательство Теоремы 3.1. ■
С помощью Теоремы 3.1 легко можно доказать следующее
Утверждение 3.2. Последовательность (a), определённая для всех n ∈N формулой ![]() , при α>0, β, C ∈ R является ILCS.
, при α>0, β, C ∈ R является ILCS.
Утверждение 3.2 имеет следующее (см. [2, c. 536‑537]) следствие:
Утверждение 3.3. Во множестве Ω бесконечно больших чисел ILN нет ни наибольшего, ни наименьшего бесконечно большого числа.
Используя Теорему 3.1, можно доказать следующие свойства для предельных значений ![]() не ограниченных конечным числом функций f, g : R → R (
не ограниченных конечным числом функций f, g : R → R ( ![]() ∈ Ω ), определив тем самым алгебру во множестве Ω:
∈ Ω ), определив тем самым алгебру во множестве Ω:
Утверждение 3.4. ![]() ,
, ![]() ;
; ![]() , С ≠ 0.
, С ≠ 0.
Утверждение 3.5. 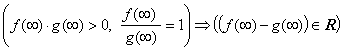 .
.
Утверждение 3.6. ![]() .
.
Утверждение 3.7. 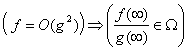 .
.
Утверждение 3.8. Если C ∈ R и C >0, то ![]() .
.
Утверждение 3.8 позволяет корректно определить бесконечно малые числа, почти также как это сделано в [1, c. 8-11, 23 и далее].
СПИСОК ЛИТЕРАТУРЫ:
- 1. Гордон Е.И., Кусраев А.Г., Кутателадзе С.С. Инфинитезимальный анализ. Ч. 1. - Новосибирск: Изд-во Ин-та математики, 2001
- 2. Степанов В.В. // Математический сборник, Т. 30 (1918), вып. 4. - С. 535.
- 3. Sukhotin A.M. Alternative analysis principles: Study. - Tomsk: TPU Press, 2002.
- 4. Sukhotin A.M. From G. Galilei's paradox to alternative analysis // 4ecm, List of posters, Section 13.13 (Real analysis), Stockholm, 2004.
- 5. Сухотин А.М. Начало высшей математики. Томск: Изд-во ТПУ, 2004.
- 6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: Наука, Гл. ред. физ.-мат. лит., 1969.-Т. 3.
- 7. Weisstein Eric W. CRC Concise Encyclopedia of Mathematics. 2nd ed. - London-New York: Chapman&Hall/CRC, 2002.



