Введение
Технический прогресс и эффективность производства в современном машиностроении неразрывно связаны с широким применением различных механизмов. Появление новых механизмов, методов их создания и проектирования является весьма актуальной задачей.
Известно [1], что в зависимости от числа общих наложенных связей все механизмы делятся на пять семейств. На механизмы нулевого семейства не накладывается ни одной общей связи, на механизмы первого семейства накладывается одна общая связь, для механизмов второго семейства число связей равно двум, для третьего – трем, для четвертого – четырем.
К настоящему времени классически пространственные механизмы нулевого семейства, плоские и сферические механизмы третьего семейства, клиновые и винтовые механизмы четвертого семейства получили достаточное распространение в технике и являются наиболее изученными в теории механизмов по сравнению с пространственными механизмами первого и второго семейств. Настоящая работа посвящена исследованию механизмов второго семейства.
Одним из основных этапов создания любого механизма является выбор его пространства функционирования. Целью настоящей работы является разработка пространств функционирования механизмов второго семейства. Методы исследования основаны на принципах теории структурного синтеза механизмов при использовании универсальной структурной формулы подвижности В. В. Добровольского [4]. В соответствии с этой формулой, записываемой в виде
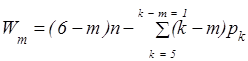 (1)
(1)
где Wm – подвижность механизма, определяющая число его степеней свободы, m – число общих наложенных связей, n – число подвижных звеньев механизма, k – класс кинематических пар от 5 до 1, создаваемые механизмы могут существенно отличаться друг от друга по комплексам движений, воспроизводимых их звеньями. Параметр m в формуле (1) означает не только числа общих связей, накладываемых на движение всего механизма в целом, но и геометрию пространств [2], в которых могут функционировать механизмы различных семейств.
Кинематическая цепь, собранная из твердых тел – звеньев, соединенных в кинематические пары без наложенных на нее общих связей, есть цепь самоустанавливающаяся [3]. Она работает в пространстве ВПВПВП (рис. 1), где стрелками вдоль (П) и вокруг (В) координатных осей обозначены поступательные и вращательные движения звеньев кинематической цепи. Всего таких независимых движений шесть – по два относительно каждой из осей координат x, y, z. Именно записью ВПВПВП отображается полный состав движений свободного тела в трехмерном декартовом пространстве.

Рис. 1. Пространство ВПВПВП, в котором работает самоустанавливающаяся (m=0) кинематическая цепь
Механизмы, работающие в пространстве ВПВПВП, относят к «классически» пространственным или адаптивным и их называют нулевыми или нулевого семейства по И. И. Артоболевскому.
Общее число свобод движения звеньев в этом случае определяется произведением 6n, где n – число звеньев кинематической цепи. Звенья цепи могут соединяться между собой посредством разных кинематических пар от пятиподвижных – первого класса р1 до одноподвижных – пятого класса р5, каждая из которых накладывает на относительные движения звеньев по одной, две, три, четыре или пять связей. Общее число связей в цепи определяется суммой (р1+2р2+3р3+4р4+5р5). Цепь оказывается подвижной, если число свобод 6n за вычетом всех наложенных связей (р1+2р2+3р3+4р4+5р5) становится более нуля. Если эта разница равна единице, то рассматриваемая система является механизмом, в нем все звенья движутся по заданным траекториям и ничто не препятствует их относительным движениям. Именно поэтому такой механизм называют адаптивным или самоустанавливающимся.
Движение звеньев механизмов первого семейства ограничивается в пространстве одной общей связью (m=1). Такие механизмы принуждаются к работе в двух различных пространствах ВПВПП и ВПВПВ. В пространстве ВПВПП (рис. 2а) устраняется вращательное движение (В), а в пространстве ВПВПВ (рис. 2b) – поступательное движение (П) относительно одной из осей.
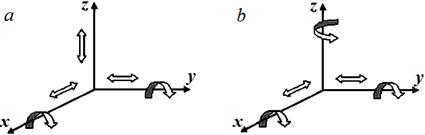
Рис. 2. Пространства функционирования механизмов первого семейства (m=1): a – ВПВПП; b – ВПВПВ
На движение звеньев механизмов второго семейства накладывается два общих условия связи (m=2), и их структурная формула подвижности (1) принимает вид
![]() (2)
(2)
где р3, р4, р5 – числа кинематических пар третьего, четвертого и пятого классов.
Два общих условия связи в механизмах второго семейства могут быть наложены различным образом, путем исключения движений ПП, ПВ, ВВ или ВП. В этих случаях кинематические цепи принуждаются к движению в пространствах, соответственно, ВПВВ, ВППВ, ВППП и ВПВП, показанных на рис. 3 a, b, c, d. В каждом из четырех названных пространств присутствуют движения ВП, под которыми следует понимать, что они возможны относительно одной и той же координатной оси. Под движениями ПВ понимается, что они воспроизводятся относительно разных осей координат [6].
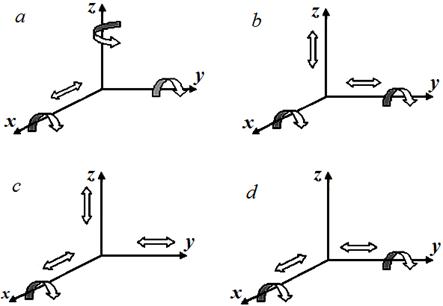
Рис. 3. Пространства функционирования механизмов второго семейства (m=2): a – ВПВВ; b – ВППВ; c – ВППП; d – ВПВП
Обратимся к анализу пространств функционирования механизмов второго семейства. В пространстве ВПВВ, показанном на рис. 3а, разрешенными являются вращательные движения звеньев вокруг всех трех осей координат и поступательное движение относительно одной из осей. Невозможными движениями оказываются поступательные движения ПП вдоль двух из осей.
Примером механизма, работающего в пространстве ВПВВ, может служить пространственный трехзвенный механизм, показанный на рис. 4a. Связав этот механизм с трехмерной системой декартовых координат, определим, что в нем вращательные движения вокруг осей х и z возможны за счет применения кинематической пары звеньев 3–1, являющейся парой четвертого класса с комплексом движений ВВ. Вращательное и поступательное движения вокруг и вдоль оси у достигаются применением в механизме цилиндрической кинематической пары звеньев 2–3. В механизме запрещены движения ПП, а именно, поступательные движения вдоль осей х и z.
Пространство ВППВ (рис. 3b) обеспечивает вращательное и поступательное движения относительно двух осей координат. При этом относительно одной из осей возможными являются оба движения. Запрещенными движениями, в этом случае, оказываются движения ПВ. Винто–рычажный механизм для перемещения коромысла [1], приведенный на рис. 4b, работает в пространстве ВППВ. В нем вокруг осей кинематических пар звеньев 1–2, 2–3 и 3–4, параллельных между собой и параллельных оси х, обеспечивается вращательное движение. Поступательное движение механизма вдоль оси z обеспечивается движением звеньев 2 и 3. Винтовое движение относительно оси у возникает за счет применения винтовой кинематической пары звеньев 4–5. Таким образом, в механизме запрещенными являются движения ПВ – поступательное вдоль оси х и вращательное вокруг оси z.
В пространстве ВППП (рис. 3с) разрешены поступательные движения вдоль всех трех осей координат, а также вращательное движение относительно одной из осей. Запрещенными являются два вращательных движения ВВ. Обратимся к пространственному рычажно-винтовому механизму [1], показанному на рис. 4c. Звено 4 механизма движется поступательно вдоль оси z. Поступательное движение вдоль оси x обеспечивается за счет применения в механизме кинематических пар звеньев 2–3 и 3–4. Винтовое движение относительно оси у, совпадающей с осью А, воспроизводится посредством винтовой кинематической пары 1–2. Таким образом, пространственный рычажно-винтовой механизм работает в пространстве ВППП. В нем запрещены вращательные движения вокруг осей z и х, то есть движения ВВ.
В механизмах, работающих в пространстве ВПВП (рис. 3d), разрешены пары движений ВП относительно двух из осей декартовой системы координат, а запрещенной является пара движений относительно третьей оси. Таким образом, запрещены движения ВП. Примером механизма, работающего в пространстве ВПВП, служит пространственный четырехзвенный механизм второго семейства, изображенный на рис. 4d [5]. В этом механизме относительно оси z обеспечивается винтовое движение за счет применения винтовой кинематической пары звеньев 4–1; поступательное движение вдоль оси у достигается за счет движения звена 3 относительно звена 4, входящих в цилиндрическую кинематическую пару четвертого класса; вращательное движение вокруг оси у в механизме осуществляется за счет поворота звена 2. Относительно оси х никаких движений нет. Таким образом, в рассматриваемом механизме запрещено движение ВП.
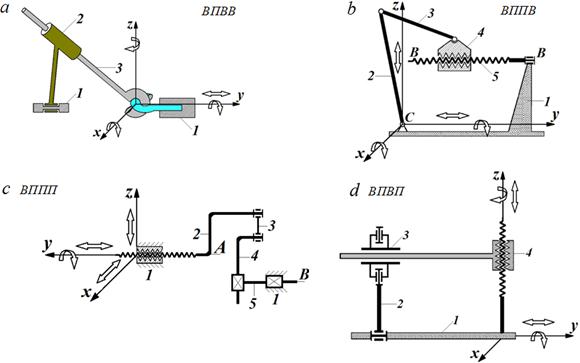
Рис. 4. Механизмы второго семейства, работающие в пространствах
ВПВВ, ВППВ, ВППП и ВПВП: a – пространственный трехзвенный механизм; b – винто-рычажный механизм для перемещения коромысла; c – пространственный рычажно-винтовой механизм; d – пространственный четырехзвенный механизм второго семейства
Заключение
Из изложенного выше следует, что все механизмы второго семейства могут работать только в четырех отличающихся пространствах: ВПВВ, ВППВ, ВППП или ВПВП. При этом механизмы, построенные в названных пространствах, имеют принципиальные отличия друг от друга. Соответственно, методы исследования таких механизмов должны быть разными и разрабатываться отдельно для каждого из пространств.
Рецензенты:
Каледин Валерий Олегович, д.т.н., профессор, действительный член Международной Академии наук высшей школы, декан факультета информационных технологий Новокузнецкого института (филиала) ФГБОУ ВПО «Кемеровский государственный университет», г. Новокузнецк.
Живаго Эдуард Яковлевич, д.т.н., профессор, заведующий кафедрой теоретической механики, ФГБОУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.



