Квантовая криптография является принципиально новым этапом в развитии информационной защиты, базирующейся на принципе детектирования одиночных фотонов наноструктурами. Основываясь на фундаментальных физических законах, квантовая криптография позволяет создавать абсолютную защиту шифрованных данных от взлома.
Долгое время, начиная с 1970-х годов, когда была высказана первая идея о возможности использования квантовых состояний для защиты информации, квантовая криптография существовала только на уровне лабораторных исследований. Развитие волоконной техники и создание в конце 1980-х годов коммерческого оптического волокна, имеющего потери менее 0.3 дБ/км, значительно стимулировало развитие квантовой криптографии и ориентировало ее на использование именно оптического волокна для передачи информации. Развитие оптоволоконной квантовой криптографии привело в 2002 году к созданию первых коммерческих квантово-криптографических систем связи (компания IdQuantique [3]), которые, однако, не получили в настоящее время широкого распространения вследствие ограничения максимально возможного расстояния при передаче шифрованной информации, которое составляло несколько десятков километров, а также вследствие невысокой скорости передачи информации.
Указанные проблемы связаны как с потерями, возникающими в оптоволокне при передаче сигнала, так и с характеристиками используемых однофотонных детекторов. Фактически максимальное расстояние передачи информации определяется предельно допустимым соотношением сигнал/шум (или количеством возникающих ошибок приема) в линии связи. И если на величину затухания сигнала влияет тип используемого волокна, то уровень шума задается типом используемого детектора. Отметим, что в настоящее время развитие технологии создания оптических волокон позволило реализовать коммерчески доступное оптическое волокно с коэффициентом затухания равным 0.170 дБ/км при предельном минимальном значении в 0.154 дБ/км (на длине волны 1.55 мкм), обусловленным инфракрасным поглощением и рэлеевским рассеянием в кварце. Таким образом, дальнейшее совершенствование оптических волокон не может привести к значительному увеличению дальности квантово-криптографической линии связи.
В настоящее время развитие квантовой криптографии идет по двум основным направлениям. Первое связано с совершенствованием протоколов при передаче шифрованной информации. На этом пути наилучшим достижением считается реализация в 2005 году квантово-криптографической системы с предельной дальностью связи в 122 км. Второе направление – совершенствование однофотонных детекторов на основе наноструктур. Значительным стимулированием этого направления являлось открытие в 2001 году эффекта однофотонного детектирования сверхпроводниковыми наноструктурами излучения ИК диапазона и создание практических приемных устройств – сверхпроводниковых однофотонных детекторов (SSPD – superconducting single photon detectors) [5]. SSPD обладает высокой квантовой эффективностью (30%) на длинах волн 1300 и 1550 нм, уровнем темнового счета менее 10 Гц, субнаносекундной длительностью импульса, обеспечивающей максимальную скорость счета более 1 Ггц, нестабильностью переднего фронта импульса (джиттер) 16 пс и высокой эффективностью согласования с одномодовым оптоволокном.
С появлением нового типа однофотонных детекторов многими ведущими зарубежными научно-исследовательскими группами, работающими в области квантовой криптографии, были экспериментально продемонстрированы значительные успехи в увеличении максимального расстояния и скорости передачи шифрованной информации. В настоящее время при использовании SSPD рекордной является передача квантового ключа на расстояние в 250 км при скорости в несколько десятков кбит/с [4], что в несколько раз превосходит параметры квантово-криптографических систем, реализованных с использованием полупроводниковых лавинных диодов. Несомненно, что SSPD имеют все перспективы стать основным типом детекторов, использующимся в квантово-криптографических линиях связи.
Одним из вариантов развития SSPD для нужд квантовой криптографии является его адаптация для работы с протоколами, в которых кодировка осуществляется числом фотонов в импульсе. В 2008 г. были созданы практические сверхпроводниковые детекторы с разрешением числа фотонов в импульсе (PNR-SSPD) [1], принцип действия которых основан на неравновесных процессах, происходящих при поглощении фотона в сверхпроводящих наноструктурах – длинных и узких (70-100 нм) полосках ультратонкой пленки (4 нм), нанесенной на диэлектрическую подложку, в присутствии тока, близкого к критическому [5].
PNR-SSPD представляет собой структуру, состоящую из одинаковых секций полосок в виде меандра, соединенных параллельно и подключенных к контактным площадкам через полосковые резисторы. Площадь детектора 10x10 мкм2. Механизм возникновения импульса напряжения следующий: по полоске сверхпроводника протекает постоянный электрический ток, плотность которого близка к критической. При поглощении фотона в небольшой области полоски сверхпроводимость подавляется и появляется «горячее пятно», при этом происходит перераспределение тока и его плотность превышает критическую. Т.к. полоска очень узкая, «горячее пятно» перекрывает сечение полоски и возникает резистивная область, что сопровождается импульсом напряжения. В течение небольшого времени «горячее пятно» исчезает, сверхпроводимость восстанавливается, и детектор вновь готов к регистрации очередного фотона.
В момент поглощения фотона в одной из полосок появляется сопротивление. Благодаря кинетической индуктивности, которой обладают полоски, резистивная полоска не шунтируется остальными, оставшимися в сверхпроводящем состоянии, полосками, что приводит к возникновению напряжения на всей структуре. Если в двух полосках одновременно поглощаются фотоны, напряжение на структуре будет больше, создавая больший по амплитуде импульс напряжения в линии передачи. Если три фотона поглощаются тремя полосками, импульс напряжения будет еще больше, и т.д. Это дает возможность различать число поглощенных фотонов по амплитуде возникающего отклика. Последовательно с каждой полоской включен пленочный резистор, изготовленный из несверхпроводящего металла. Резисторы необходимы для ограничения тока и препятствуют одновременному переключению нескольких полосок при поглощении одного фотона. Импульсы фотооткликов, соответствующих различному числу поглощенных фотонов, имеют различные амплитуды напряжения. С увеличением числа фотонов в лазерном импульсе вероятность наблюдения отклика с большей амплитудой возрастает [5].
Ниже, в качестве первого шага, будет рассмотрено применение PNR-SSPD в классических линиях связи с точки зрения минимизации числа фотонов в импульсе при сохранении приемлемо низкой доли ошибочных битов BER (bit error ratio). Чтобы в протяженных линиях связи, содержащих множество усилителей и мультиплексоров, накопленная ошибка не превысила допустимую норму, BER каждого устройства должна быть не выше 10-11. Основными фактором, определяющим уровень ошибок соединения, является чувствительность и быстродействие приемного модуля оптического терминала. Применяемые в настоящее время лучшие p-i-n диоды и лавинные фотодиоды обеспечивают BER на уровне 10-10–10-12 в оптическом интерфейсе 2,5–9,95 Гбит/с при чувствительности -28 дБм и -15 дБм соответственно. Это означает, что каждый бит информации передается оптическим импульсом, содержащим 104-105 фотонов. Чувствительность приемников ограничивает длины оптоволоконных линий связи между ретрансляторами. Наименьшим ослаблением оптического сигнала обладают оптоволоконные линии на одномодовых волокнах, но и в таких магистралях мощность передаваемых импульсов ослабляется в среднем в 100 раз на каждые 100 км. Актуальной, таким образом, является разработка высокочувствительных приёмных модулей, способных обеспечивать требуемые BER при работе с предельно слабыми сигналами.
Число фотонов в оптическом импульсе, необходимое для достижения требуемой BER при использовании PNR-SSPD в качестве детектора приёмного модуля, может быть оценено следующим образом. При регистрации сообщения возникают ошибки двух типов, замены логической «1» на логический «0» и логического «0» на логическую «1». Их вероятности обозначим соответственно BER10 и BER01. Обе вероятности зависят не только от числа фотонов в импульсе и эффективности детектора, но и от уровня дискриминации M – числа отсчётов детектора, принимаемого в качестве граничного значения между «0» и «1». При слишком низком значении уровня дискриминации велико число ошибок ложной регистрации «1» в логическом «0», при слишком высоком – велико число ошибок пропуска логической «1». Минимальной BER при числе фотонов в импульсе N соответствует выполнение условия BER10+BER01=min, т.е.
![]() ,(1)
,(1)
где Nd=N/SNR – среднее число фотонов в фазе логического «0», SNR – отношение сигнал/шум линии. Для современных линий стандартом является отношение мощностей, соответствующих уровням логического нуля и логической единицы, не менее 18 дБ, что соответствует SNR=60, поэтому Nd<<N.
В предположении, что число параллельных секций детектора достаточно велико, вероятность регистрации m фотонов при среднем числе фотонов в импульсе N даётся распределением Пуассона
![]() ,(2)
,(2)
где n=ηN – среднее число зарегистрированных фотонов, η – эффективность детектирования. Тогда вероятности BER10 и BER01, в соответствии со своими определениями, выражаются через Pm(n) формулами
![]() ,(3а)
,(3а)
![]() ,(3b)
,(3b)
Условие минимума по M сводится к равенству![]() , которое выполняется при
, которое выполняется при
![]() .(4)
.(4)
Учитывая, что благодаря большой величине SNR M в несколько раз меньше ηN, можно заменить сумму в (3a) её наибольшим членом и с логарифмической точностью написать
![]() ,
,
откуда, учитывая (4), получаем для ηN оценку по порядку величины
![]() ,
,
или
![]() ,(5)
,(5)
![]() .
.
Поправочный множитель при больших отношениях сигнал/шум близок к единице и при выполнении оценок может быть опущен (при SNR=60 он равен 1.5).
Для лучших стандартных SSPD (работающих только в однофотонном режиме) величина η достигает 30%. Полагая η=0.1, получаем, что для достижения BER на уровне 10-11 требуется иметь в оптическом импульсе ≈ 400 фотонов, что в среднем на 2 порядка меньше, чем при использовании существующих приёмных модулей.
Формула (5) говорит о логарифмическом характере зависимости числа фотонов, которое необходимо иметь в импульсе, от требуемой доли ошибочных битов, и даёт оценку N по порядку величины. Однако для точного вычисления N мы выполнили численные расчёты непосредственно на основании формул (3). Результаты расчётов зависимости BER от уровня дискриминации, числа фотонов в импульсе и отношения сигнал/шум приведены на рис. 1. Видно, что требуемый уровень BER=10-11 достигается при 55 отсчётах в импульсе (и при M=13), что при η=0.1 соответствует 550 фотонам в импульсе. Зависимость минимально достижимой BER от числа фотонов близка к экспоненциальной, что соответствует аналитике (5), при этом количественное расхождение с оценкой по формуле не превосходит 40%. Эти численные результаты подтверждает пригодность простой формулы (5) для выполнения оценок эффективности PNR-детектора в качестве приёмного модуля телекоммуникационной линии.
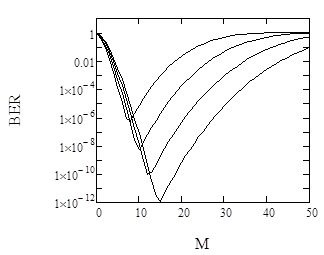
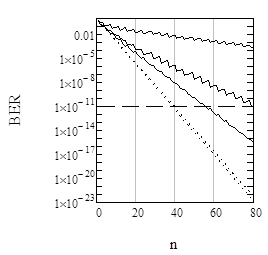
Рис. 1. Левая панель – зависимость доли ошибочных битов от уровня дискриминации (отношение сигнал/шум положено равным 18 дБ). Среднее число регистрируемых фотонов n=ηN в фазе логической «1» составляет (сверху вниз): 30; 40; 50; 60. Правая панель – зависимость минимально достижимой доли ошибочных битов (соответствующей оптимальному уровню дискриминации) от среднего числа регистрируемых фотонов. Сплошные кривые – численный расчёт, пунктир – формула (5). Отношение сигнал/шум составляет (сверху вниз) 10 дБ; 15 дБ; 18 дБ. Для аналитических кривых зависимость от отношения сигнал/шум несущественна. Мелкомасштабная немонотонность рассчитанных зависимостей связана с дискретностью уровня дискриминации. Пунктирная линия – BER=10-11.
Таким образом, применение PNR-SNPD позволит значительно снизить количество необходимых ретрансляторов в оптических передающих линиях связи благодаря увеличению не менее чем в 102 раз чувствительности приемных модулей.
Научные исследования проведены при финансовой поддержке Минобрнауки России (госконтракт № 11.519.11.4011, соглашение № 14.B37.21.0246) и гранта Президента Российской Федерации, договор № 16.120.11.4005-МК от 01.02.2012.
Рецензенты:
Куприянов М.Ю., д.ф.-м.н., профессор, г.н.с., Научно-исследовательский институт ядерной физики им. Д.В. Скобельцина МГУ им. М.В. Ломоносова, г. Москва.
Вдовин В.Ф., д.ф.-м.н., в.н.с., Институт прикладной физики РАН, г. Нижний Новгород.



