Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Современное российское архитектурное образование находится в стадии реформирования [7, 8]. В данной работе проведен статистический анализ российского архитектурно-строительного образования в начале XXI века на основе вступительных испытаний, в значительной степени опирающихся на результаты ЕГЭ как критерий оценки качества работы средней школы и качества набора абитуриентов в высшую школу [1, 2] с привлечением иногда для анализа методов математической статистики [6]. Рейтинг вузов РФ по среднему баллу ЕГЭ (mЕГЭ) [4], показывающий уровень знаний абитуриентов 2012 года, поступивших на бюджетные места в  государственные вузы страны, возглавляет МГИМО, у которого средний балл ЕГЭ – 92,3 по 100 балльной шкале, а среди государственных архитектурно-строительных вузов (АСВ) лидирует Уральская ГАХА (76,9) – 33-е место среди 491 вуза. В табл. 1 из показателей вступительных испытаний (ПВИ) кроме mЕГЭ приведены также разность mЕГЭ между 2012 и 2011 гг. (Dm), долевое количество абитуриентов (в % от общего количества бюджетных мест), принятых по конкурсу баллов ЕГЭ (NЕГЭ), по олимпиадам (NО), по льготам (NЛ) и по целевому набору (NЦ). Заметим, что подсистема долевых показателей является избыточной, так как NЕГЭ+NЦ+NО+NЛ =100 %.

Таблица 1. ПВИ 2012 г. государственных архитектурно-строительных университетов (ГАСУ) и архитектурно-художественных академий (ГАХА)

Согласно табл. 1, NО практически равно нулю. Данное обстоятельство должно вызывать тревогу в рамках креативного подхода к архитектурному образованию [7].

В работах [3, 5] рассмотрено применение метода классификации вузов на мировом. В данной работе этот метод применен на федеральном уровне для классификации российских АСВ по совокупности ПВИ 2011–2012 гг. (табл. 1). Составляющими статистического метода исследования являются корреляционный, кластерный и дисперсионный анализы. Статистический анализ проводился в системе Statistica [9]. В силу разнородности ПВИ они были стандартизированы.

Результаты проверки ПВИ на корреляционную зависимость (матрица коэффициентов парных корреляций) приведены в табл. 2 (Пирсона r – в право-верхнем треугольнике над диагональю и Спирмена R – в лево-нижнем треугольнике под диагональю). Жирным шрифтом выделены статистически значимые корреляции: положительная между NЛ и NЦ, отрицательные – между NЕГЭ и NЦ, а также NЕГЭ и NЛ. Наличие корреляционной связи долевых ПВИ позволяет уменьшить их количество до одного (основного NЕГЭ) и провести дальнейший анализ в трехмерном пространстве ПВИ: {mЕГЭ, Dm,  NЕГЭ}.

Таблица 2. Матрица коэффициентов парных корреляций Пирсона r и ранговых корреляций Спирмена R ПВИ

При проведении кластеризации АСВ в построенном трехмерном пространстве {mЕГЭ, Dm,  NЕГЭ} в качестве меры близости выбрано евклидово расстояние, а в качестве правила объединения двух кластеров использован метод Уорда. Методом древовидной кластеризации построено иерархическое дерево (рис. 1).

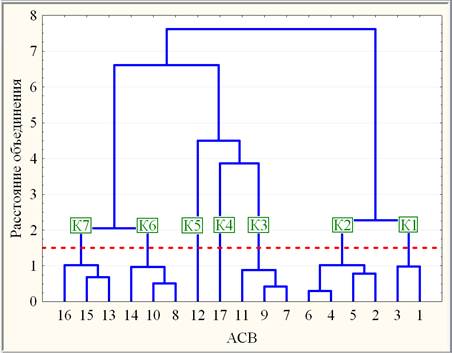
Рис. 1. Дендрограмма АСВ в пространстве {mЕГЭ, Dm, NЕГЭ}

В зависимости от выбора расстояния объединения можно получить соответствующее число кластеров. Так, например, расстоянию объединения, равного 1,5 (красная пунктирная горизонтальная прямая), соответствует 7 кластеров (К1-7), расстоянию объединения, равного 5, соответствует 3 кластера (К1+К2, К3+ К4+К5, К6+К7). Таким образом, выбор значения связующего расстояния позволяет проводить кластеризацию на любом уровне, то есть строить кластерную модель с любым  наперед заданным числом кластеров.

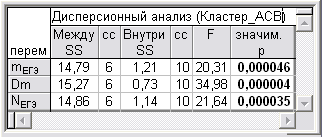
Наряду с методом древовидной кластеризации применяется также метод K-средних, проводящий классификацию объектов (АСВ) по заданному количеству кластеров. Предлагается семикластерная высококачественная модель АСВ, согласно λ-критерию Уилкса высоко значимо (на уровне значимости р < 0,000005)  различающая 7 кластеров АСВ по совокупности mЕГЭ, Dm и NЕГЭ.  Качество кластеризации АСВ по каждому ПВИ оценено посредством параметрического дисперсионного анализа (табл. 3) как высоко значимое (на уровне значимости р < 0,00005). Заметим, что согласно критериям непараметрического дисперсионного анализа (ранговому критерию Краскела-Уоллиса и медианному тесту) качество кластеризации АСВ по каждому ПВИ оценивается как статистически значимое (на уровне значимости 0,01 < р < 0,05).

Таблица 3. Результаты дисперсионного анализа кластеризации АСВ по каждому ПВИ

После получения результатов классификации рассчитываются средние значения показателей по каждому кластеру (рис. 2) для оценивания значимости их различий между собой.

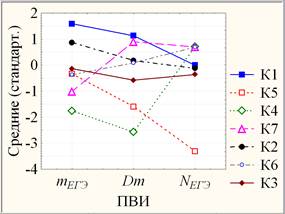
Рис. 2. Графики средних значений ПВИ по каждому кластеру

Для каждого ПВИ согласно апостериорному критерию наименьших значений разности (НЗР), ранговому критерию Краскела-Уоллиса и медианному тесту можно выделить однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) группы кластеров (рис. 2), расположенные в порядке убывания средних:

Ø mЕГЭ: {К1}, {К2}, {К3, К5, К6}, {К4}, {К7}. При этом, например,  {К2} отличается от {К3, К5, К6} сильно значимо по НЗР  (уровень значимости 0,001 < р < 0,01) и статистически значимо по критерию Краскела-Уоллиса и по медианному тесту (уровень значимости 0,01 < р < 0,05).

Ø Dm (рис. 3): {К1, К7}, {К2, К6}, {К3}, {К5}, {К4}. При этом, например, {К1, К7} и {К2, К6} различаются сильно значимо по НЗР и по медианному тесту (уровень значимости 0,001 < р < 0,01), а по критерию Краскела-Уоллиса различаются статистически значимо (0,01 < р < 0,05).

Ø NЕГЭ (рис. 4):  {К4, К6, К7}, {К1, К2, К3}, {К5}. При этом, например, по НЗР  К1 отличается от К6 и К7 также, как К2 от К4 на уровне значимости  р≈0,05, а {К4, К6, К7} и {К1, К2, К3} различаются статистически значимо по критерию Краскела-Уоллиса (уровень значимости 0,01 < р≈0,038 < 0,05) и по медианному тесту (уровень значимости 0,01 < р≈0,023< 0,05).

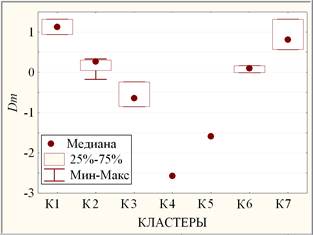
Рис. 3. Диаграмма размаха для каждого кластера по Dm

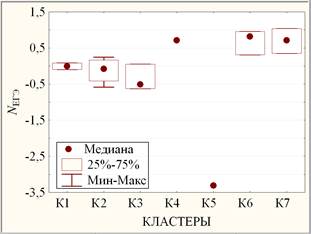
Рис. 4. Диаграмма размаха для каждого кластера по NЕГЭ

Графики средних кластеров в рамках семи кластерной модели АСВ представлены диаграммой рассеяния средних кластеров АСВ в трехмерном пространстве {mЕГЭ, Dm,  NЕГЭ} в виде образной формы «храма потенциального высшего архитектурно-строительного образования» (рис. 5).  Как было замечено выше (табл. 1), практически отсутствует  «олимпиадная» составляющая фундамента «храма», необходимая в рамках креативного подхода к архитектурному образованию [7], что порождает ощущение неполноценности и неустойчивости всего сооружения.

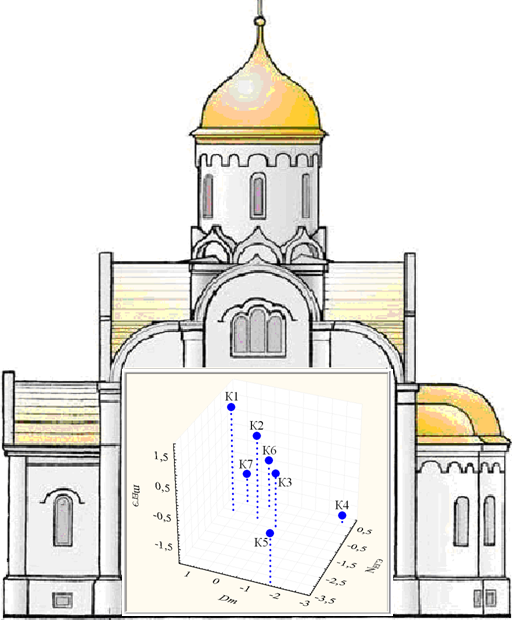
Рис. 5.  «Храм потенциального архитектурно-строительного образования»

Результаты кластерного анализа АСВ по совокупности показателей (рис. 2–5) позволяют провести качественную классификацию АСВ в номинальной шкале измерений (табл. 4), полагая в качестве уровня «Средний» – стандартизированный интервал (-0,5; +0,5) для ПВИ. Аномально высокие значения (> +2,0) определяют уровень «Лидер», а аномально низкие значения (< -2,0) определяют уровень «Аутсайдер». Промежуточные значения между средними и аномальными значениями определяют уровень «Выше среднего» и «Ниже среднего» соответственно.

Таблица 4. Качественная классификация АСВ

Выводы

1. Особенностью системы показателей вступительных испытаний 2012 г. в российские архитектурно-строительные вузы является практически нулевое долевое количество абитуриентов (в % от общего количества бюджетных мест), принятых по олимпиадам.

2. На основании корреляционного анализа показателей вступительных испытаний в архитектурно-строительные вузы выявлена высоко значимая наиболее сильная отрицательная корреляционная зависимость между долевым количеством абитуриентов, принятых по конкурсу баллов ЕГЭ и по целевому набору.

3. В рамках кластерного анализа в трех мерном пространстве ПВИ построена кластерная модель архитектурно-строительных вузов, позволяющая проводить кластеризацию на любом уровне, т. е. строить кластерную модель с любым  наперед заданным числом кластеров, что дает возможность выделять группы архитектурно-строительных вузов, однородных по совокупности факторных показателей.

4. Подробно рассмотрена высоко значимая семикластерная модель. Для каждого показателя выделены группы однородных кластеров. На основе результатов кластеризации проведена качественная классификация АСВ.

5. Результаты подобной кластеризации вузов могут быть учтены в рамках проходящей реформы высшего образования, например, при финансировании вузов или сокращении их количества.

Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.

Рецензенты:

Трифонов Андрей Юрьевич, д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский томский политехнический университет, г. Томск.

Арефьев Константин Петрович, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский томский политехнический университет, г. Томск.