В последние годы отмечается тенденция проявления особого интереса к автономным источникам энергии (далее АИЭ), подтверждением чего является появление значительного количества зарубежных и отечественных публикаций и патентов. Данный интерес объясняется тем, что с помощью малогабаритных и легких электромеханических преобразователей энергии (далее – ЭМПЭ), дополненных выпрямителями, накопительными конденсаторами и преобразователями напряжения, можно обеспечивать энергией портативные мобильные устройства при отсутствии централизованной сети питания промышленной частоты. Особое внимание заслуживают ЭМПЭ колебательного движения, которые позволяют использовать окружающую нас механическую энергию вибраций, толчков и т.п. Наиболее целесообразно использовать для этих целей ЭМПЭ с постоянными магнитами [6], так как при этом нет потерь энергии на возбуждения магнитного поля, что существенно повышает КПД устройств данного типа. Так, например, автономные ЭМПЭ колебательного движения с постоянными магнитами могут служить источником питания светодиодных ламп в цехах машиностроительных предприятий, используя энергию вибраций здания, станков. Также можно освещать мосты, преобразовывая кинетическую и потенциальную энергии моста в электрическую. Либо подзаряжать КПК, мобильный телефон во время вашей ходьбы.
На рисунке 1 представлена оригинальная конструкция электромеханического преобразователя [1] и общая схема построения АИЭ на основе трехкоординатного колебательного электромеханического преобразователя (далее – ТКЭП), где ЭПР – элемент преобразования и распределения, Н – нагрузка, ЭН – накопительный элемент.
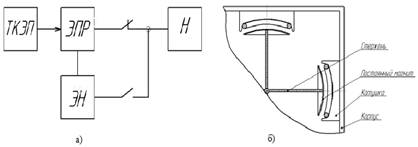
Рис. 1: а) структурная схема автономного источника энергии;
б) трехкоординатный электромеханический преобразователь колебательного движения.
Элемент преобразования и распределения включает в себя электронный блок, содержащий выпрямитель, накопитель и преобразователь уровней напряжения, и распределительный блок, обеспечивающий передачу электрической энергии потребителю.
Накопительный элемент позволяет аккумулировать электроэнергию при работе без нагрузки и выдавать её потребителю в период интенсивного потребления или при неработающем ЭМПЭ.
Анализ структурной схемы показывает, что основной частью АИЭ является сам ТКЭП. Следовательно, от выходных характеристик и параметров ТКЭП зависят требования, предъявляемые к АИЭ. А значит выбор конструктивной схемы ТКЭП является важным вопросом при разработке подобных систем.
Предлагаемый электромеханический преобразователь [1] содержит корпус, индукционную систему из подвижной и неподвижной частей. Подвижная часть выполнена в виде двухполюсных постоянных магнитов, закрепленных на упругих стержнях. Неподвижная часть состоит из катушек, размещенных по периметру корпуса. Это позволяет ЭМПЭ обеспечивать преобразование энергии возмущений внешней среды любого направления (например, вибраций) в электрическую энергию при уменьшении габаритов и массы ЭМПЭ. Наиболее важным моментом при проектировании подобных электромеханических преобразователей является исследование ЭДС катушки и индукции в воздушном зазоре при установившемся режиме. В связи с этим задачей данной работы является разработка математической модели, описывающей электромагнитные процессы при установившемся режиме ТКЭП, и ее анализ.
Решение поставленной задачи сводилось к наиболее полному отражению реальной картины электромагнитного поля ТКЭП. Известные аналитические и графические методы исследования электромагнитного поля обладают значительной сложностью, что является причиной наложения множества допущений при расчетах, а следовательно, и снижением их точности. Наиболее точным методом решения задач подобного класса является численный анализ методами компьютерного моделирования. Численное решение определяется для конкретных габаритных размеров, что также ограничивает его применение. В связи с этим в работе использовался метод расчета электромагнитного поля, представляющий собой симбиоз математических методов и методов компьютерного моделирования.
На рисунке 2а представлена расчетная схема ТКЭП, на рисунке 2б – результаты компьютерного моделирования картины электромагнитного поля в программном комплексе Ansys.
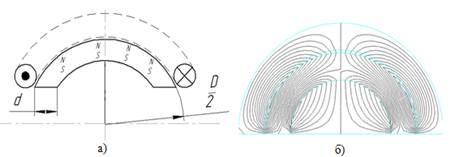
Рис. 2: а) расчетная схема колебательного контура;
б) картина электромагнитного поля ТКЭП.
Анализ полученной картины распределения магнитного поля (рис. 2б) показал, что в центре активного элемента магнитная индукция ТКЭП равняется нулю, а по мере удаления от центра она возрастает.
Ввиду сложности математического моделирования систем с постоянными магнитами активная система ТКЭП представляется в виде токового витка, тогда магнитная индукция на поверхности активной части ТКЭП принимается в виде [4]:
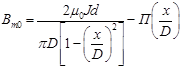
,(1)
где 
– намагниченность постоянного магнита; 
– диаметр постоянного магнита; 
– толщина постоянного магнита; 
– координата точки измерения магнитной индукции на поверхности постоянного магнита; 
– полный эллиптический интеграл 2 рода [2].
С целью качественного анализа (1) в среде MathCAD была построена зависимость магнитной индукции на поверхности ТКЭП от координаты (рис. 3).
Качественный анализ полученной зависимости (рис. 4), показал: в центре активного элемента магнитная индукция ТКЭП равняется нулю, по мере удаления от центра она возрастает. То есть данные математического расчета подтверждают данные компьютерного моделирования.
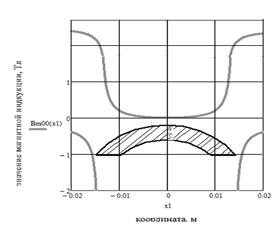
Рис. 3. Распределение магнитной индукции на поверхности ТКЭП.
При движении активной части ТКЭП происходит изменение активного диаметра магнитной системы, тогда:
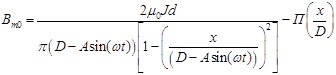
, (2)
где 
– закон изменения координаты при колебаниях
Магнитный поток холостого хода ТКЭП [3] определяется в виде:
, (3)
где 
– эффективная площадь обмотки; 
– магнитный поток в воздушном зазоре; 
– коэффициент рассеяния.
Эффективная площадь обмотки принимается в виде:
, (4)
где 
– диаметр кривизны обмотки, 
– центральный угол окружности, определяющий сектор обмотки; 
– осевая длина обмотки.
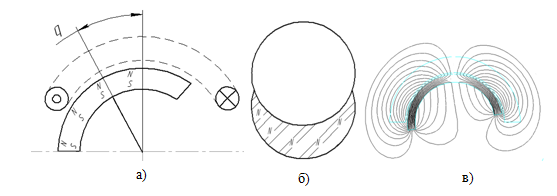
Рис. 4: а) расчетная схема колебательного контура при движении;
б) ТКЭП вид сверху; в) картина электромагнитного поля ТКЭП при движении.
С учетом того что при движении активной части генератора происходит изменение эффективной площади обмотки и перераспределение магнитных потоков (рис. 5 а, б), то площадь обмотки, а следовательно и магнитный поток, принимаются в виде:
,(5)
, (6)
где 
– координата смещения активной части.
Слагаемое 
представляет собой магнитный поток, который рассеивается при выходе постоянного магнита за пределы обмотки.
Координата колебаний постоянного магнита принимается в виде:
, (7)
Тогда магнитный поток генератора при холостом ходе определяется как функция угловой координаты колебаний в виде:
, (8)
Магнитная индукция в воздушном зазоре ТКЭП при холостом ходе определяется в виде:
,(9)
Скорость движения активного элемента ТКЭП [5] определяется в виде:
, (10)
Дифференцирование (10) с учетом (7) определяет скорость подвижного элемента:
. (11)
Так как в установившемся режиме амплитуда колебаний определяется двумя составляющими, ЭДС в установившемся режиме определяется в следующем виде:
(12)
(13)
Таким образом, разработана математическая модель ЭДС ТКЭП в установившимся режиме.
С целью оценки адекватности разработанной математической модели в программном комплексе Mathcad были произведены численные расчеты. Результаты расчетов представлены на рисунке 5.
При увеличении амплитуды колебаний до 50% воздушного зазора ТКЭП зависимость ЭДС от времени движения имеет несинусоидальный характер и при этом значение ЭДС возрастает в 100 раз (рис. 5а). При амплитуде колебаний до 95% воздушного зазора заметно увеличивается несинусоидальность ЭДС, разность амплитуд между соседними пиками составляет 30% (рис. 5б), при этом ЭДС возрастает в 10 раз.
При частоте колебаний 90,7 Гц зависимость ЭДС от времени движения имеет несинусоидальный характер, разность между минимальным и максимальным пиками составляет 5-7% (рис. 5д). При увеличении частоты колебаний на 41% несинусоидальность ЭДС увеличивается, разность между максимальным и минимальным пиком составляет 15-20%, значение ЭДС увеличивается на 65,88% (рис. 5ж). При уменьшении частоты колебаний на 43% несинусоидальность ЭДС сохраняется с разностью между минимальным и максимальным пиками 2-3%, при этом ЭДС снижается на 50% (рис. 5е).
Адекватность полученных результатов подтверждает их схожесть с результатами других авторов [2], причем данные результаты получены иными методами для однокоординатного ЭМПЭ линейного возвратно-поступательного движения.
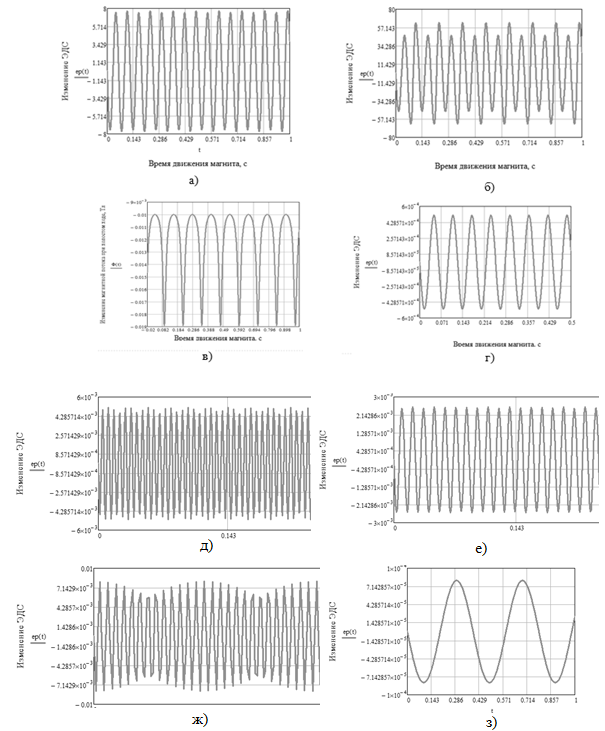
Рис. 5: а) зависимость ЭДС ТКЭП при амплитуде, равной 50% воздушного зазора;
б) зависимость ЭДС ТКЭП при амплитуде, равной 95% воздушного зазора;
в) зависимость магнитного потока ТКЭП при амплитуде, равной 95% воздушного
зазора;
г) зависимость ЭДС ТКЭП при амплитуде, стремящейся к нулю;
д) зависимость ЭДС ТКЭП от частоты колебаний, частота 90,7 Гц;
е) зависимость ЭДС ТКЭП от частоты колебаний, частота 39,8 Гц;
ж) зависимость ЭДС ТКЭП от частоты колебаний, частота 127,4 Гц;
з) зависимость ЭДС ТКЭП от частоты колебаний, частота 1,27 Гц.
Разработана математическая модель, описывающая электромагнитные и электромеханические процессы при установившемся режиме ТКЭП, и проведена качественная проверка посредством компьютерного моделирования в программном комплексе Ansys.
Полученные результаты могут быть использованы на практике при проектировании одно-, двух- и трехкоординатных электромеханических преобразователей энергии колебательного движения.
Рецензенты:
Ураксеев М.А., д.т.н., профессор кафедры ИИТ ФГБОУ ВПО «УГАТУ», г. Уфа.
Гизатуллин Ф.А., д.т.н., профессор кафедры ЭМ ФГБОУ ВПО «УГАТУ», г. Уфа.