Описываемое помольное устройство (рис. 1) состоит из неподвижного корпуса бочкообразной формы 1, изготовленного из эластичного материала, в который после деформирования поместили мелющие тела 2. Ролики 4, закрепленные на водиле 3, обкатывают корпус, тем самым перемещают мелющие тела, таким образом, материал интенсивно измельчается ввиду большого количества точечных контактов.
Используя принципы механики сплошной среды [1], можно определить силовые характеристики, действующие на загрузку в помольной камере.
Принимаем допущения:
1) рассматриваемая среда (мелющие тела в смеси с измельчаемым материалом) однородна по всему объему;
2) скорость вращения водила с обкатывающими роликами или частота воздействий, имитирующих вращение водила, является постоянной, что соответствует установившимся режимам работы мельницы и движению среды;
3) системой отсчета является ось неподвижного деформируемого корпуса, и движение частиц по отношению к этой системе отсчета принимается за абсолютное.
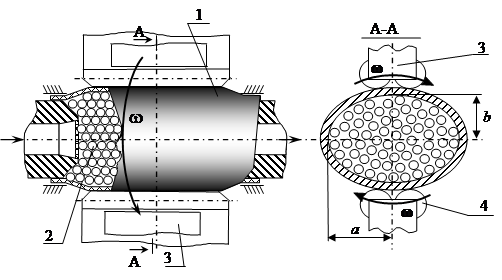
Рис. 1. Схема устройства с рабочей камерой бочкообразной формы, деформируемой в поперечном сечении вращением
Рассмотрим кинематику движения точки ![]() вокруг оси неподвижной камеры в поперечном сечении (при относительном перемещении) вследствие воздействия на нее обкатывающих роликов.
вокруг оси неподвижной камеры в поперечном сечении (при относительном перемещении) вследствие воздействия на нее обкатывающих роликов.
Предположим, что в результате обкатывающего движения роликов любая точка будет совершать в плоскости YOZ движение по окружности с радиусом r (рис. 1) [4], изменяющимся в диапазоне ![]() ; здесь а – большая полуось эллиптической части деформированной рабочей камеры.
; здесь а – большая полуось эллиптической части деформированной рабочей камеры.
Для описания движения точек загрузки (смесь мелющих тел и материала) введем в плоскости YOZ полярную систему координат ![]() , где полярный угол
, где полярный угол ![]() отсчитывается от положительного направления оси Y (рис. 2, а). Изменение, которое со временем задается линейной функцией времени
отсчитывается от положительного направления оси Y (рис. 2, а). Изменение, которое со временем задается линейной функцией времени ![]() , здесь
, здесь ![]() – угловая скорость вращения материальной точки.
– угловая скорость вращения материальной точки.
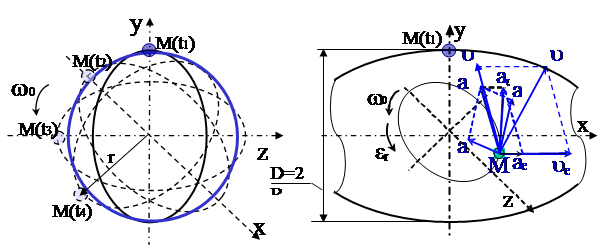
а) б)
Рис. 2. Расчетная схема движения материальной точки М в рабочей камере бочкообразной формы
Для перехода из полярной системы координат в декартовую воспользуемся соотношениями [2]:
![]() (1)
(1)
![]() (2)
(2)
где ![]() ,
, ![]() – декартовые координаты точки в момент времени
– декартовые координаты точки в момент времени ![]() ;
;
![]() – радиус кругового движения мелющих тел.
– радиус кругового движения мелющих тел.
Для обоснования и проведения анализа сил, действующих на загрузку в рабочей камере, предположим, что при деформировании камеры в поперечном сечении вращением мелющие тела в основном осуществляют движение по траектории согласно рисунку 2. По данной расчетной схеме действуют силы Fn, Fe и Fτ. (рис. 3).
К материальной точке ![]() (рис. 3) массы
(рис. 3) массы ![]() , движущейся по окружности со скоростью
, движущейся по окружности со скоростью ![]() , приложена сила
, приложена сила ![]() , направление которой образует с вектором скорости
, направление которой образует с вектором скорости ![]() некоторый угол. Точка, при этом, будет двигаться с ускорением, сонаправленным с силой
некоторый угол. Точка, при этом, будет двигаться с ускорением, сонаправленным с силой ![]() . Ускорение можно разложить на составляющие:
. Ускорение можно разложить на составляющие: ![]() и
и ![]() . Аналогично силу
. Аналогично силу ![]() раскладываем на составляющие: касательную силу
раскладываем на составляющие: касательную силу ![]() , изменяющую модуль скорости точки (сила трения возникает при относительном сдвиге шаровой загрузки по отношению к внутренней поверхности помольной камеры и обусловлена действием касательной силы
, изменяющую модуль скорости точки (сила трения возникает при относительном сдвиге шаровой загрузки по отношению к внутренней поверхности помольной камеры и обусловлена действием касательной силы ![]() ) и нормальную
) и нормальную ![]() , изменяющую направление скорости точки (сила трения возникает при относительном сдвиге смежных секториальных слоев шаровой загрузки и обусловлена действием распорной силы
, изменяющую направление скорости точки (сила трения возникает при относительном сдвиге смежных секториальных слоев шаровой загрузки и обусловлена действием распорной силы ![]() ) [7].
) [7].
Результирующая сил ![]() и
и ![]() есть центробежная сила инерции
есть центробежная сила инерции ![]() .
.
В механике дисперсных сред установлено [6], что действующая в элементарном слое величина центробежной силы инерции ![]() связана с величинами распорных усилий следующей зависимостью:
связана с величинами распорных усилий следующей зависимостью:
![]() (3)
(3)
где ![]() – коэффициент распорного усилия [5].
– коэффициент распорного усилия [5].
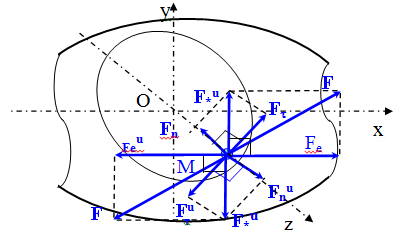
Рис. 3. Схема основных сил сопротивления действующих на материальную точку ![]()
Сила трения ![]() возникает при относительном сдвиге смежных секториальных слоев загрузки и обусловлена действием распорной силы.
возникает при относительном сдвиге смежных секториальных слоев загрузки и обусловлена действием распорной силы.
Выделим в рабочей камере элементарный объем ![]() , тогда его масса равна:
, тогда его масса равна:
![]() (4)
(4)
где ![]() – объемная плотность загрузки;
– объемная плотность загрузки;
![]() – отношение объема мелющих тел к объему рабочей камеры;
– отношение объема мелющих тел к объему рабочей камеры;
![]() – плотность мелющих тел;
– плотность мелющих тел;
![]() – плотность материала.
– плотность материала.
Элементарная сила ![]() , действующая на элементарный объем в приближении парного взаимодействия, равна:
, действующая на элементарный объем в приближении парного взаимодействия, равна:
![]() (5)
(5)
Сила ![]() во всем объеме камеры определяется:
во всем объеме камеры определяется:
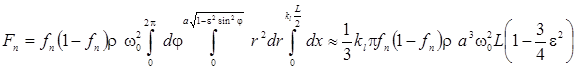 (6)
(6)
где ![]() – коэффициент трения скольжения материала мелющих тел (шаров) по измельчаемому материалу [3];
– коэффициент трения скольжения материала мелющих тел (шаров) по измельчаемому материалу [3];
kl – коэффициент отношения длины дуги камеры к длине камеры ![]() .
.
![]() – сила трения, возникающая при относительном сдвиге шаровой загрузки по отношению к внутренней поверхности рабочей камеры и обусловленная действием касательной силы
– сила трения, возникающая при относительном сдвиге шаровой загрузки по отношению к внутренней поверхности рабочей камеры и обусловленная действием касательной силы ![]() .
.
Элементарная сила ![]() , действующая на элементарный объем
, действующая на элементарный объем ![]() , равна:
, равна:
![]() (7)
(7)
где ![]() – коэффициент трения скольжения материала мелющих тел по материалу камеры [3].
– коэффициент трения скольжения материала мелющих тел по материалу камеры [3].
При определении ![]() можно считать, что расстояние от центра траектории до точки М шарового слоя равно
можно считать, что расстояние от центра траектории до точки М шарового слоя равно ![]() , а масса мелющих тел равна массе шарового слоя, прилегающего к стенке камеры. Поэтому сила
, а масса мелющих тел равна массе шарового слоя, прилегающего к стенке камеры. Поэтому сила ![]() может быть определена по формуле:
может быть определена по формуле:
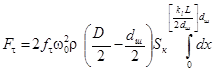 (8)
(8)
где ![]() – целое число, равное количеству шаров.
– целое число, равное количеству шаров.
Площадь кольца из шаров, расположенных вдоль корпуса, задается выражением:
![]() (9)
(9)
где ![]() – количество шаров в кольце, определяемое следующими соотношениями:
– количество шаров в кольце, определяемое следующими соотношениями:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Тогда окончательно сила ![]() во всем объеме камеры определяется выражением:
во всем объеме камеры определяется выражением:
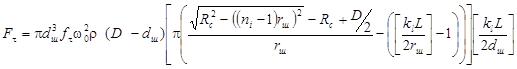 (14)
(14)
![]() – сила трения, возникающая при переносном перемещении шаровой загрузки вдоль камеры, обусловлена силой
– сила трения, возникающая при переносном перемещении шаровой загрузки вдоль камеры, обусловлена силой![]()
![]() , возникающей вследствие неоднородности сечения камеры по длине, которая является векторной суммой сил:
, возникающей вследствие неоднородности сечения камеры по длине, которая является векторной суммой сил:
![]() (15)
(15)
Элементарная сила![]()
![]() , действующая на элементарный объем
, действующая на элементарный объем ![]() , равна:
, равна:
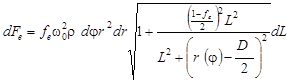
где ![]() – коэффициент трения скольжения материала мелющих тел по измельчаемому материалу [3].
– коэффициент трения скольжения материала мелющих тел по измельчаемому материалу [3].
Сила ![]() во всем объеме
во всем объеме ![]() рабочей камеры определяется:
рабочей камеры определяется:
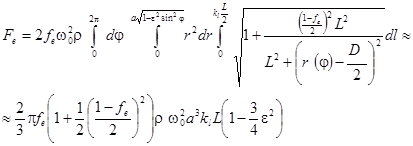 (17)
(17)
Вычисление интеграла (17) осуществлялось, приближенно используя метод малого параметра, по которому производилось разложение подынтегральной функции в ряд с учетом, что в данном случае ![]() .
.
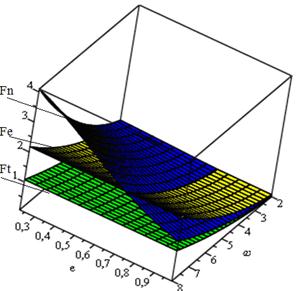
Рис. 4. График зависимости сил Fe, Fn, Fτ (желтый – Fe, синий – Fn, зеленый – Fτ,), действующих на загрузку от частоты вращения привода в камерах, деформируемых в поперечном сечении вращением
(R=0,05 м; L=0,2 м)
Для схем деформирования в поперечном сечении вращением наибольшее значение имеют силы (рис. 4): Fe (возникает при перемещении загрузки вдоль камеры) и Ft (возникает при сдвиге мелющих тел и материала по отношению к внутренней поверхности рабочей камеры, ее величина в основном обусловлена размером мелющих тел и коэффициентом трения материала мелющих тел по материалу внутренней поверхности камеры). Характер изменения силы Fn показывает на то, что при увеличении степени деформирования интенсивность перемещения загрузки в центральной зоне также будет увеличиваться, но при увеличении размеров камеры и уменьшении размеров мелющих тел в центральной зоне может образоваться мертвая зона, что нужно учитывать при проектировании помольных устройств большего типоразмера.
Рецензенты:
Трубаев Павел Алексеевич, д.т.н., доцент, зав. кафедрой теплоэнергетики, теплогазоснабжения и вентиляции, НОУ ВПО «Белгородский инженерно-экономический институт», г. Белгород.
Уваров Валерий Анатольевич, д.т.н., профессор, зав. кафедрой теплогазоснабжения и вентиляции Белгородского государственного технологического университета
им. В. Г. Шухова, г. Белгород.



