Введение.
Существуют множество химических, биологических, физико-химических и физических показателей, определяющих качество речной воды [1; 5; 6] по видам загрязнения. Нами приняты для моделирования многолетние ежемесячные данные Аналитического центра контроля качества воды МУП «Водоканал» г. Йошкар-Ола в общем случае с 10.06.2002 по 08.12.2011 г. на пробах из водозабора реки Малая Кокшага (табл. 1).
Таблица 1 – Результаты лабораторных испытаний (фрагмент)
|
№ п/п |
Дата
|
Время T, сут
|
Цветность, градус |
Мутность, мг/л |
РН |
Сухой остаток, мг/л |
Жесткость., моль/л |
… |
Калий + Натрий, мг/л |
Кальций, моль/л |
Магний, мг/л |
Марганец, мг/л |
Цинк, мг/л |
|
1 |
2 |
3 |
4 |
5 |
… |
21 |
22 |
23 |
24 |
25 |
|||
|
1 |
10.06.2002 |
0 |
22 |
3.1 |
7.9 |
241.0 |
3.68 |
… |
- |
2.57 |
- |
0.01 |
0.0037 |
|
2 |
04.07.2002 |
24 |
11 |
7.7 |
7.6 |
233.0 |
3.66 |
… |
- |
2.38 |
- |
0.008 |
0.008 |
|
3 |
07.08.2002 |
58 |
20 |
4.5 |
7.7 |
216.8 |
3.54 |
… |
- |
2.3 |
- |
0.03 |
0.003 |
|
4 |
09.09.2002 |
91 |
18 |
2.8 |
7.9 |
218.2 |
3.86 |
… |
- |
2.38 |
- |
0.006 |
0.001 |
|
5 |
30.10.2002 |
142 |
25 |
4.98 |
7.8 |
236.0 |
3.8 |
… |
- |
2.49 |
- |
0.01 |
0.002 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
21 |
10.08.2011 |
3348 |
41 |
2.9 |
8.1 |
228 |
4.1 |
… |
10.5 |
2.6 |
18.3 |
0.031 |
0.0018 |
|
22 |
07.09.2011 |
3376 |
24 |
2.6 |
8 |
226 |
4.1 |
… |
11.8 |
2.5 |
19.52 |
0.044 |
0.0013 |
|
23 |
12.10.2011 |
3411 |
27 |
1.5 |
8 |
245 |
4.5 |
… |
0.5 |
2.5 |
24.4 |
0.032 |
0.0017 |
|
24 |
14.11.2011 |
3444 |
21 |
1.90 |
7.9 |
253.0 |
4.6 |
… |
21.00 |
2.9 |
18.30 |
0.082 |
0.0012 |
|
25 |
08.12.2011 |
3468 |
19 |
1.54 |
7.4 |
285.0 |
5.0 |
… |
6.50 |
3.3 |
20.74 |
0.094 |
0.0028 |
В таблице 1 представлены результаты по 25 показателям, включающие органолептические и показатели химического состава воды, по которым проводились регулярные испытания. Шкала времени принята по суткам с началом от даты первого измерения. Тогда относительно этой шкалы абсцисс можно идентифицировать закономерности динамики загрязнения по каждому его виду. Аналитический центр проводил испытания речной воды по 46 показателям, из них достаточно заполненными по измеренным значениям были 25 параметров, а измерения по ![]() и
и ![]() стали проводить с января 2009 года.
стали проводить с января 2009 года.
Модель динамики загрязнения. Математическим моделированием [3; 4] получена общая модель изменения гидрохимического показателя во времени (1)
![]() (1)
(1)
![]() ,
,
![]()
![]() ,
,
где ![]() – гидрохимический показатель;
– гидрохимический показатель; ![]() – первая составляющая, показывающая по закону экспоненциального роста или гибели естественную часть динамического процесса;
– первая составляющая, показывающая по закону экспоненциального роста или гибели естественную часть динамического процесса; ![]() – вторая составляющая динамики загрязнения речной воды по каждому виду загрязнителя, которая показывает стрессовое возбуждение загрязнителя со временем (в некоторых видах загрязнения этой составляющей может и не быть);
– вторая составляющая динамики загрязнения речной воды по каждому виду загрязнителя, которая показывает стрессовое возбуждение загрязнителя со временем (в некоторых видах загрязнения этой составляющей может и не быть); ![]() – волновая составляющая изменения содержания гидрохимического показателя;
– волновая составляющая изменения содержания гидрохимического показателя; ![]() – номер волновой составляющей формулы (1);
– номер волновой составляющей формулы (1); ![]() – количество волновых составляющих в статистической модели, шт.;
– количество волновых составляющих в статистической модели, шт.; ![]() – параметры статистической модели (1), определяемые в программной среде CurveExpert по статистической выборке из данных таблицы 1.
– параметры статистической модели (1), определяемые в программной среде CurveExpert по статистической выборке из данных таблицы 1.
Эта программная среда имеет максимальное число неизвестных параметров модели 19, поэтому для повышения уровня адекватности уравнений требуется специальная программа.
Пример. Для примера покажем изменение концентрации в речной воде химическим веществом ![]() за период 26.01.2009 – 08.12.2011 г. По обобщенной модели (1) нами были выявлены детерминированная закономерность, а также три модели с волновыми функциями в виде асимметричных вейвлет-сигналов.
за период 26.01.2009 – 08.12.2011 г. По обобщенной модели (1) нами были выявлены детерминированная закономерность, а также три модели с волновыми функциями в виде асимметричных вейвлет-сигналов.
Детерминированная факторная зависимость без учета второй составляющей (1) с небольшим коэффициентом корреляции ![]() слабой тесноты связи имеет вид:
слабой тесноты связи имеет вид:
![]() (2)
(2)
Дополнительно статистическим моделированием получили формулу с одной волной:
![]() (3)
(3)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
где ![]() – первая составляющая роста концентрации
– первая составляющая роста концентрации ![]() ;
; ![]() – вторая составляющая равна нулю;
– вторая составляющая равна нулю; ![]() – третья составляющая колебательного возмущения;
– третья составляющая колебательного возмущения;![]() – половина амплитуды колебательного возмущения;
– половина амплитуды колебательного возмущения; ![]() – половина периода волнового изменения содержания
– половина периода волнового изменения содержания ![]() в речной воде.
в речной воде.
Следующая модель получена исходя из вычислительных возможностей программной среды. При наращивании формулы (2) получили уравнение из четырех составляющих:
![]() (4)
(4)
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() – четвертая составляющая колебательного возмущения;
– четвертая составляющая колебательного возмущения;![]() – половина амплитуды колебательного возмущения четвертой составляющей;
– половина амплитуды колебательного возмущения четвертой составляющей; ![]() – половина периода волнового изменения четвертой составляющей;
– половина периода волнового изменения четвертой составляющей; ![]() – пятая составляющая колебательного возмущения;
– пятая составляющая колебательного возмущения; ![]() – половина амплитуды колебательного возмущения пятой составляющей;
– половина амплитуды колебательного возмущения пятой составляющей; ![]() – половина периода волнового изменения пятой составляющей.
– половина периода волнового изменения пятой составляющей.
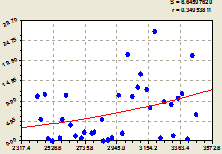
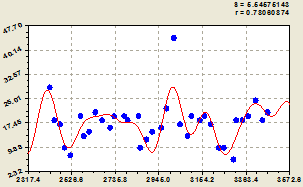
На рисунке 1 представлен график изменения концентрации калия и натрия за 1047 суток.
|
|
|
|
|
а |
б |
в |
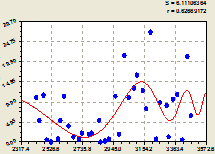
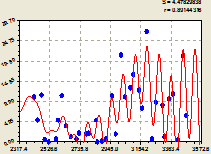
Рис. 1. Изменение содержания ![]() : а – детерминированная модель (2); б – модель с одной волновой составляющей (3); в – модель (4) по возможностям программной среды
: а – детерминированная модель (2); б – модель с одной волновой составляющей (3); в – модель (4) по возможностям программной среды
Изменение содержания калия и натрия в речной воде лучше всего характеризует модель (4), коэффициент корреляции которой составил 0.8914. Из рисунка 1в видно, что на 2736 сутки (декабрь 2009 года) концентрация в речной воде была наименьшей, затем содержание ![]() увеличивалось и достигло в начале 2011 года максимальных значений.
увеличивалось и достигло в начале 2011 года максимальных значений.
Анализ результатов. Коэффициент корреляции (табл. 2) позволяет оценить адекватность полученных закономерностей.
|
Таблица 2 – Коэффициент корреляции между переменными факторами [3] |
||||||||||||||||||
|
|
||||||||||||||||||
|
Для этого нами проставлены ранги по убыванию значений коэффициента корреляции. Ранг приняли равным нулю для самой высокоадекватной закономерности по модели (1), фактический коэффициент корреляции которой составил 0.8914 (изменение концентрации![]() в речной воде).
в речной воде).
В таблице 3 показана адекватность ![]() закономерностей по модели (1).
закономерностей по модели (1).
Таблица 3 – Коэффициенты корреляции модели (1) по разной структуре идентификации
|
Показатели |
Коэффициент корреляции модели (1) |
Кратность |
|||||||
|
тренд
|
ранг
|
с одной волной
|
ранг
|
с вол- нами
|
ранг
|
|
|
ранг |
|
|
Цветность, градус |
0.1639 |
50 |
0.3767 |
41 |
0.5082 |
29 |
2.3 |
3.1 |
5 |
|
Мутность, мг/л |
0.2305 |
46 |
0.4887 |
31 |
- |
- |
2.1 |
- |
- |
|
pH |
0.4694 |
34 |
0.7719 |
6 |
- |
- |
1.6 |
- |
- |
|
Сухой остаток, мг/л |
0.0000 |
59 |
0.5482 |
25 |
0.7372 |
9 |
|
|
|
|
Жесткость, моль/л |
0.1267 |
52 |
0.5775 |
20 |
- |
- |
4.6 |
- |
- |
|
Щелочность общая, моль/л |
0.0533 |
58 |
0.5006 |
30 |
0.7725 |
5 |
9.4 |
14.5 |
0 |
|
Окисляемость перм., мгО/л |
0.1937 |
48 |
0.5723 |
22 |
0.6543 |
15 |
3.0 |
3.4 |
4 |
|
БПК-20, мгО/л |
0.2815 |
44 |
0.4192 |
37 |
0.5532 |
24 |
1.5 |
2.0 |
7 |
|
Взвешенные вещества, мг/л |
0.1852 |
49 |
- |
- |
- |
- |
- |
- |
- |
|
АСПАВ, мг/л |
0.4228 |
36 |
0.6195 |
18 |
- |
- |
1.5 |
- |
- |
|
Нефтепродукты, мг/л |
0.1263 |
53 |
0.4776 |
33 |
- |
- |
3.8 |
- |
- |
|
Фенолы, мг/л |
0.6943 |
11 |
0.7803 |
4 |
0.8363 |
1 |
1.1 |
1.2 |
10 |
|
Аммоний солевой, мг/л |
0.2391 |
45 |
0.3499 |
42 |
- |
- |
1.5 |
- |
- |
|
Нитриты, мг/л |
0.3960 |
38 |
0.5425 |
27 |
- |
- |
1.4 |
- |
- |
|
Нитраты, мг/л |
0.1424 |
51 |
0.6761 |
13 |
- |
- |
4.7 |
- |
- |
|
Сульфаты, мг/л |
0.4844 |
32 |
0.6162 |
19 |
0.7385 |
8 |
1.3 |
1.5 |
8 |
|
Фосфаты, мг/л |
0.4534 |
35 |
0.5480 |
26 |
- |
- |
1.2 |
- |
- |
|
Фториды, мг/л |
0.5606 |
23 |
0.6906 |
12 |
0.7334 |
10 |
1.2 |
1.3 |
9 |
|
Хлориды, мг/л |
0.0749 |
56 |
0.6503 |
16 |
0.7529 |
7 |
8.7 |
10.1 |
1 |
|
Железо общее, мг/л |
0.0737 |
57 |
- |
- |
- |
- |
- |
- |
- |
|
Калий + натрий, мг/л |
0.3495 |
43 |
0.6267 |
17 |
0.8914 |
0 |
1.8 |
2.6 |
6 |
|
Кальций, моль/л |
0.0886 |
55 |
0.5326 |
28 |
0.6722 |
14 |
6.0 |
7.6 |
2 |
|
Магний, мг/л |
0.0000 |
59 |
0.5762 |
21 |
0.7806 |
3 |
|
|
|
|
Марганец, мг/л |
0.1123 |
54 |
0.3798 |
40 |
0.7813 |
2 |
3.4 |
7.0 |
3 |
|
Цинк, мг/л |
0.2107 |
47 |
0.3900 |
39 |
- |
- |
1.9 |
- |
- |
Из таблицы 3 видно, что слабую связь имеют закономерности с одной составляющей, среднюю – с одной волновой составляющей и сильную – закономерности, принимающие конструкцию модели (1).
В таблице 3 также показана кратность: отношение коэффициентов корреляции закономерности с одной волновой составляющей ![]() к тренду
к тренду ![]() и отношение коэффициентов корреляции уравнений с волнами
и отношение коэффициентов корреляции уравнений с волнами ![]() к тренду
к тренду ![]() .
.
Ранговое распределение адекватности моделей. Для оценки погрешности закономерностей нами проведено ранжирование значений коэффициентов корреляции.
Закономерность изменения коэффициента корреляции в зависимости от рангового распределения (рис. 2) имеет вид:
![]() , (5)
, (5)
где ![]() – значение коэффициента корреляции;
– значение коэффициента корреляции; ![]() – ранг.
– ранг.
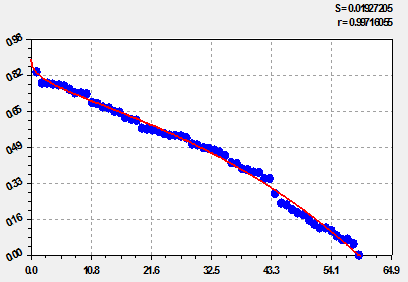
Рис. 2. Ранговое распределение коэффициентов корреляции.
Из рисунка 2 следует, что с повышением требований к адекватности, по росту значений коэффициента корреляции ![]() , число уравнений медленно сокращается.
, число уравнений медленно сокращается.
Изменение кратности коэффициентов корреляции (рис. 3) происходит по формуле:
![]() , (6)
, (6)
где ![]() – кратность;
– кратность; ![]() – ранг.
– ранг.
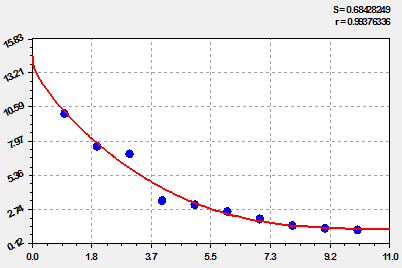
Рис. 3. Ранговое распределение кратности коэффициентов корреляции.
Максимальное значение кратности составляет 14.5, то есть в 14.5 раз закономерность динамики щелочности с волновыми составляющими (![]() ) точнее тренда (
) точнее тренда (![]() ). Незначительно происходит повышение адекватности с волновыми составляющими по динамике фенола, здесь
). Незначительно происходит повышение адекватности с волновыми составляющими по динамике фенола, здесь ![]() , а
, а ![]() .
.
В случаях когда тренд принимает среднеарифметическое значение и коэффициент корреляции по тренду ![]() равен 0.0000 (сухой остаток и магний), кратность принимает значение
равен 0.0000 (сухой остаток и магний), кратность принимает значение ![]() .
.
Сравнение концентрации загрязнения с ПДК. Известно, что основным критерием загрязнения воды являются предельно-допустимые концентрации [1; 2]. ПДК для магния в воде водных объектов хозяйственно-питьевого и культурно-бытового водопользования составляет 50 мг/л [2].
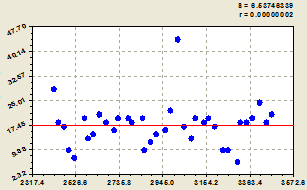
На рисунке 4а показано среднеарифметическое значение концентрации магния в речной воде, равное ![]() мг/л, то есть тренд не показывает динамику магния.
мг/л, то есть тренд не показывает динамику магния.
|
|
|
|
а |
б |
Рис. 4. Сравнение с ПДК: а – тренд; б – общая модель (7).
На рисунке 4б представлена общая модель содержания магния в речной воде (7), где видно, что концентрация магния за период наблюдений не превысила ПДК=50 мг/л.
![]() (7)
(7)
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В формуле (7) первая составляющая упростилась по конструкции до постоянного члена.
Из рисунка 4б заметны колебания концентрации магния. Содержание магния в поверхностных водах меняется в течение года: максимальные концентрации наблюдаются в меженный период, минимальные – в период половодья [1].
Заключение. Закономерности с волновыми составляющими колебательного возмущения получают высокие значения критерия тесноты связи. Выявленные закономерности показали, что тренд имеет грубую точность, но она может быть применена для ориентировочных расчетов, а также для составления прикидочных рекомендаций производству.
А модель с волновыми составляющими с наименьшей погрешностью показывает динамику загрязнения речной воды. Наибольший коэффициент корреляции равен 0.8914 у модели с четырьмя составляющими, из которых три – волновые, что больше в 2.6 раза коэффициента корреляции по тренду. Поэтому сложные по конструкции модели будут полезными для формулировки научных выводов.
Рецензенты:
Винокурова Раиса Ибрагимовна, д-р биол. наук, профессор, заведующая кафедрой химии, Поволжский государственный технологический университет, г. Йошкар-Ола.
Салихов Мухаммет Габдухаевич, д-р техн. наук, профессор, кафедра автомобильных дорог, Поволжский государственный технологический университет, г. Йошкар-Ола.