Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Среди широкого спектра проблем современной метеорологии важное место занимает проблема восполнения информации о состоянии атмосферы на отдельных высотных уровнях в текущий момент времени, по имеющимся данным на ниже и вышележащих уровнях, а также данным, полученным в предыдущие моменты времени, т.е. процедура экстраполяции метеорологических параметров.

Область применения данной процедуры весьма широка. В частности, можно выделить задачу, связанную с лидарным дистанционным зондированием состояния атмосферы. Несмотря на преимущества лидарных систем, перед радиозондированием, есть и существенные недостатки, среди которых их зависимость от погодных условий. Так, например, при низкой сплошной облачности, тумане и интенсивных осадках оптическое зондирование атмосферы вообще не проводится. Поэтому в подобных погодных условиях (для обеспечения всепогодности лидарного зондирования) необходимо использовать один из возможных алгоритмов численной экстраполяции метеорологических полей по высоте, осуществляемой по данным наземного или нижележащих уровней.

На практике, в метеорологии, данная задача длительное время решалась на основе методов статистической экстраполяции, базирующихся на использовании уравнений множественной регрессии [2, 6, 7]. Однако эти методы дают удовлетворительные результаты лишь для атмосферных слоев небольшой толщины и при отсутствии существенных изломов в вертикальных профилях метеорологических величин [4].

Цель исследования

Целью настоящей статьи является рассмотрение результатов численной оценки    точности экстраполяции, проведенной при помощи динамико-стохастического подхода, предложенного авторами данной статьи в [3], основанного на применении двумерной динамико-стохастической модели и алгоритма фильтра Калмана.

Материал и метод исследования

Данный подход заключается в следующем. Предположим, что интересующие нас метеорологические величины непрерывно распределены в некотором пространстве. При этом объем ограничен снизу уровнем земли (рис. 1), сверху - высотой рассматриваемого слоя атмосферы H, а геометрические размеры в нижнем сечении определяются размерами, в пределах которого корреляционная функция интересующей нас метеовеличины существенным образом не изменяется.

В пределах подобного пространства произвольно размещена станция высотного зондирования, обеспечивающая измерения метеорологических величин во всем взятом атмосферном слое с разрешением по высоте Dh. Эти измерения можно представить для некоторого фиксированного момента времени tk в виде N-мерного профиля (вектора), каждая компонента которого соответствует определенному высотному уровню hi=h1, h2,, ..., H.

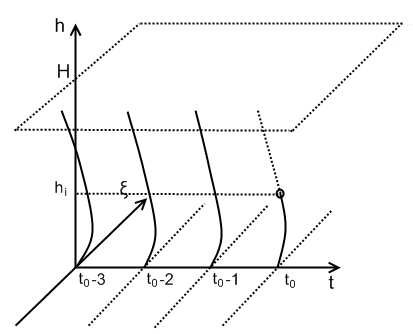
Рис. 1.  Измерения метеопараметра во времени

Задача экстраполяции любой из метеорологических величин в заданной точке пространства (х0, y0, hi) по данным единичной станции высотного наблюдения заключается в оценке его значения в фиксированный момент времени t0  по данным измерений на выше- или нижележащих уровнях и измерениям в предыдущие моменты времени с помощью некоторой математической модели [2, 6].

В качестве математической модели, используемой для решения поставленной задачи, была предложена малопараметрическая динамико-стохастическая модель [3], которая описывает зависимость изменения поля x по высоте и во времени и имеет вид:

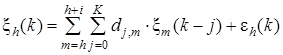                                               (1)

где  – значение поля метеовеличины на фиксированной высоте h в момент времени k; m – текущий номер высотного уровня, на котором выполняется экстраполяция, причем m меняется от h до h+i (здесь i =1, 2, …, n – максимальное число высотных уровней, данные которых учитываются при экстраполяции поля  на уровне h); j – текущее значение дискретного времени, изменяющегося от 0 до K; dj,m – неизвестные коэффициенты, подлежащие оцениванию и определяющие взаимную связь между значением поля  и его значениями в предыдущие моменты времени на заданной высоте и вышележащих высотных уровнях, т.е. ;  – невязка модели, которая определяется стохастичностью рассматриваемых атмосферных процессов.

Подобный подход позволяет уже на основе двух предшествующих высотных наблюдений и наземных данных, полученных в срок восстановления, восполнить недостающую информацию на всех заданных уровнях ПСА, причем не только в месте расположения аэрологической станции (или системы лидарного зондирования), но и во всех произвольных точках мезомасштабной области, где проводятся наземные метеорологические измерения [5].

В качестве исходных данных был взят массив двухсрочных (00 и 12 ч. по Гринвичу) радиозондовых наблюдений за январь и июль 2007–2010 гг., полученный для двух аэрологических станций: Москва (55°45¢с.ш., 37°57¢в.д) и Новосибирск (54°58¢с.ш., 82°57¢в.д), находящихся в районах с различными физико-географическими условиями. Учитывая наличие пропусков данных в радиозондовых наблюдениях, для исследования были использованы 243 профиля для  зимы и 245 профилей для лета, полученных с аэрологической станции Москва, а также 237 и 240 профилей для зимы и лета соответственно для станции в г. Новосибирск.

Расчет средних в слое значений температуры, зональной и меридиональной составляющих скорости ветра осуществлялся с помощью выражения [4]:

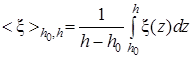,                                                                                                                     (2)

где x – метеорологическая величина, а знак <×> обозначает процедуру усреднения по вертикали в слое h-h0, где h0 и h – высота нижней и верхней границ этого слоя, причем h0=0 соответствует уровню земной поверхности.

Полагая в выражении (2) h0=0 и h=hk, где hk – высота верхней границы рассматриваемого k-го слоя атмосферы, и представляя интеграл в виде суммы, это выражение можно записать в виде:

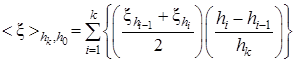,                                                                                               (3)

которое и было использовано для расчета средних в слое значений температуры, зональной и меридиональной составляющих скорости ветра.

Для реализации алгоритма калмановской фильтрации, приведенного в [3], в момент времени k=0 (момент инициализации), т.е. при полном отсутствии априорной информации, был задан ряд начальных условий, а именно:

·  начальный вектор оценивания   (т.е. модельные параметры dj,m=0), что обусловлено полным отсутствием полезной информации о поведении этих параметров;

· начальная корреляционная матрица шумов наблюдений  =, элементы которой на главной диагонали rii (при условии, что шумы eh(k) не имеют корреляционных зависимостей) приняты, исходя из величин ошибок радиозондовых наблюдений [4], равных 0,7 °С (для температуры) и 1,0 м/с (для ортогональных составляющих скорости ветра);

· начальная корреляционная матрица шумов состояния , элементы которой на главной диагонали qii (при условии, что шумы w(k) также не имеют корреляционных зависимостей) задаются равными единице, исходя из предварительного анализа поведения вектора состояния, составленного из неизвестных безразмерных параметров модели (1) [3].

Кроме того,  при расчете весовых коэффициентов Kk в линейном фильтре Калмана должна использоваться, согласно [1], ковариационная матрица ошибок оценивания  , которую также необходимо задавать в момент инициализации этого фильтра. На практике обычно задают , причем матрица  является диагональной, элементы которой на главной диагонали должны лежать в пределах Pij=1,…,100 (в нашем случае, как показал предварительный анализ,  Pij=10), а вне главной диагонали они равняются нулю.

Для оценки точности предложенного динамико-стохастического алгоритма целесообразно провести статистическую оценку, с помощью среднеквадратических погрешностей dx  вычисляемую по формуле [4]:

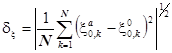         , (2)

а также вероятностей Р ошибок экстраполяции температуры и ортогональных составляющих скорости ветра менее и более заданной величины. Результаты оценки приведены в табл. 1 и 2.

Таблица 1

Среднеквадратические  погрешности dx вероятности Р(´102) ошибок экстраполяции профилей температуры и ортогональных составляющих скорости ветра менее и более заданной величины для ст. Москва

Таблица 2

Среднеквадратические  погрешности dx вероятности Р(´102) ошибок экстраполяции профилей температуры и ортогональных составляющих скорости ветра менее и более заданной величины для ст. Новосибирск

Анализ данных табл. 1 и 2 показывает, что использование алгоритма фильтра Калмана с двумерной динамико-стохастической моделью для экстраполяции профилей температуры и ортогональных составляющих  скорости ветра действительно дает для всего пограничного слоя и независимо от взятой станции хорошие и приемлемые для практики результаты. Так, например, среднеквадратические погрешности  такого восстановления не превышают значений 0,9 °С зимой и 0,6 °С летом (для температуры) и соответственно 2,5 м/с и 1,4 м/c (для зональной и меридиональной составляющих скорости ветра).

Кроме того, о высокой точности данного алгоритма говорят и значения вероятности малых ошибок экстраполяции (менее ±1°С для температуры и менее ±1 м/с для ортогональных составляющих скорости ветра). Правда, если для температуры вероятность ошибок восстановления менее ±1°С составляет во всем пограничном слое, причем независимо от взятой станции и сезона, более 0,8, то для составляющих скорости ветра вероятность ошибок менее ±1 м/с варьирует в близких пределах (более 0,64) только в летний период, зимой подобные ее значения отмечаются главным образом лишь  в слое 0–400 м.

Заключение

В заключение следует сказать, что предложенный алгоритм, основанный на двумерной динамико-стохастической модели и алгоритме фильтра Калмана, даст более точные результаты экстраполяции при использовании данных, поступающих чаще, чем два раза в сутки. Такими данными могут быть, например, измерения лидарного дистанционного зондирования, обладающего высоким временным разрешением.

Рецензенты:

Белан Борис Денисович, д.ф.-м.н., профессор, зам. директора по научной работе, Институт оптики атмосферы СО РАН, г. Томск.

Комаров Валерий Сергеевич, д.г.н., профессор, главный научный сотрудник, Институт оптики атмосферы СО РАН, г. Томск.